Argumentationsram

Se även: Argumentationsteori

Inom artificiell intelligens och relaterade områden är ett argumentationsramverk ett sätt att hantera kontroversiell information och dra slutsatser från den med hjälp av formaliserade argument .

I ett abstrakt argumentationsramverk är information på nybörjarnivå en uppsättning abstrakta argument som till exempel representerar data eller en proposition. Konflikter mellan argument representeras av en binär relation på uppsättningen av argument. Rent konkret representerar du ett argumentationsramverk med en riktad graf så att noderna är argumenten och pilarna representerar attackrelationen. Det finns några förlängningar av Dungs ramverk, som de logikbaserade argumentationsramarna eller de värdebaserade argumentationsramarna.

Abstrakta argumentationsramar

Formell ram

Abstrakta argumentationsramar, även kallade argumentationsramar à la Dung , definieras formellt som ett par:

• En uppsättning abstrakta element som kallas argument , betecknade $A$
• En binär relation på $A$ , kallad attackrelation , betecknad $R$

Grafen byggd från systemet $S$ .

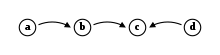
Till exempel, argumentationssystemet $S=\langle A,R\rangle$ med $A=\{a,b,c ,d\}$ och $R=\{(a,b),(b,c),(d,c) )\}$ innehåller fyra argument ( $a,b,c$ och $d$ ) och tre attacker ( $a$ attacker $b$ , ${ \displaystyle b}$ attackerar $c$ och $d$ attacker ${\displaystyle c} )$ .

Dung definierar några begrepp:

• ett argument $a\in A$ är acceptabelt med avseende på $E\subseteq A$ om och endast om $E$ försvarar $a$ , det vill säga $\forall b\in A$ så att $(b,a)\in R,\exists c\in E$ så att $(c,b)\in R$ ,
• en uppsättning argument $E$ är konfliktfri om det inte finns någon attack mellan dess argument, formellt: $\forall a,b\in E ,(a,b)\inte \i R$ ,
• en uppsättning argument $E$ är tillåtet om och endast om det är konfliktfritt och alla dess argument är acceptabla med avseende på $E$ .

Olika acceptans semantik

Tillägg

För att avgöra om ett argument kan accepteras eller inte, eller om flera argument kan accepteras tillsammans, definierar Dung flera acceptanssemantiker som tillåter att, givet ett argumentationssystem, uppsättningar av argument (kallade extensions) beräknas . Till exempel, givet $S=\langle A,R\rangle$ ,

• $E$ är en komplett förlängning av $S$ endast om det är en tillåten mängd och varje godtagbart argument med avseende på $E$ tillhör $E$ ,
• $E$ är en föredragen förlängning av $S$ endast om det är ett maximalt element (med avseende på mängdteoretisk inkludering) bland de tillåtna mängderna med avseende på $S$ ,
• $E$ är en stabil förlängning av $S$ endast om det är en konfliktfri uppsättning som attackerar varje argument som inte hör hemma i $E$ (formellt $\forall a\in A\backslash E,\exists b\in E$ så att $(b,a)\in R$ ,
• $E$ är den (unika) jordade förlängningen av $S$ endast om det är det minsta elementet (med avseende på set-inkludering) bland de kompletta tilläggen av $S$ .

Det finns några inneslutningar mellan uppsättningarna av tillägg byggda med denna semantik:

• Varje stabil förlängning är att föredra,
• Varje önskad förlängning är klar,
• Den jordade förlängningen är klar,
• Om systemet är välgrundat (det finns ingen oändlig sekvens $a_{0},a_{1},\dots ,a_{n},\dots$ så att ${\displaystyle \forall i>0,(a_{i+1},a_{i})\in R} ),$ alla dessa semantiker sammanfaller – bara en förlängningen är jordad, stabil, föredragen och komplett.

En del annan semantik har definierats.

Man introducerar notationen $Ext_{\sigma }(S)$ för att notera mängden $\sigma$ -förlängningar av systemet $S$ .

I fallet med systemet $S$ i figuren ovan, $Ext_{\sigma }(S)=\{\{a, d\}\}$ för varje Dungs semantik – systemet är välgrundat. Det förklarar varför semantiken sammanfaller, och de accepterade argumenten är: $a$ och $d$ .

Märkning

Märkning är ett mer uttrycksfullt sätt än tillägg för att uttrycka acceptansen av argumenten. Konkret är en märkning en mappning som associerar varje argument med en etikett in (argumentet accepteras), ut (argumentet avvisas) eller undec (argumentet är odefinierat – inte accepterat eller avvisat). Man kan också notera en märkning som en uppsättning par $({\mathit {argument}},{\mathit {label}})$ .

En sådan kartläggning är inte meningsfull utan ytterligare begränsningar. Begreppet återinförande märkning garanterar känslan av kartläggningen. $L$ är en återställningsmärkning på systemet $S=\langle A,R\rangle$ om och endast om:

• $\forall a\in A,L(a)={\mathit {i}}$ om och endast om $\forall b\ i A$ så att $(b,a)\in R,L(b)={\mathit {out}}$
• $\forall a\in A,L(a)={\mathit {out}}$ om och endast om $\exists b \in A$ så att $(b,a)\in R$ och $L(b)={\mathit {in}}$
• $\forall a\in A,L(a)={\mathit {undec}}$ om och endast om ${ \displaystyle L(a)\neq {\mathit {in}}}$ och $L(a)\neq {\mathit {out}}$

Man kan konvertera varje tillägg till en återställningsmärkning: argumenten för tillägget är i , de som attackeras av ett argument för tillägget är ute och de andra är undec . Omvänt kan man bygga en förlängning från en återställningsmärkning bara genom att behålla argumenten i . Caminada bevisade faktiskt att återställningsmärkningarna och de fullständiga tilläggen kan kartläggas på ett bijektivt sätt. Dessutom kan den andra Datungs semantik associeras med vissa uppsättningar av återställningsmärkningar.

Återinförande märkningar skiljer argument som inte accepteras eftersom de attackeras av accepterade argument från odefinierade argument – ​​det vill säga de som inte försvaras kan inte försvara sig. Ett argument är undec om det attackeras av åtminstone en annan undec . Om det bara attackeras av argument ut , måste det vara in , och om det attackeras något argument in , så är det ute .

Den unika återställningsmärkningen som motsvarar systemet $S$ ovan är $L=\{(a,{\mathit {in}}),(b,{\mathit {out}}),(c,{\mathit {out}}),(d,{\mathit { i}})\}$ .

Slutledning från ett argumentationssystem

I det allmänna fallet när flera tillägg beräknas för en given semantisk ${\displaystyle \sigma } ,$ kan agenten som resonerar från systemet använda flera mekanismer för att härleda information:

• Godtrogen slutledning : agenten accepterar ett argument om det tillhör minst en av $\sigma$ -tilläggen—i vilket fall riskerar agenten att acceptera några argument som inte är acceptabla tillsammans ( $a$ attacker $b$ , och $a$ och $b$ tillhör vardera ett tillägg)
• Skeptisk slutledning : agenten accepterar ett argument endast om det tillhör varje $\sigma$ -tillägg. I det här fallet riskerar agenten att härleda för lite information (om skärningspunkten mellan förlängningarna är tom eller har en mycket liten kardinal).

För att dessa två metoder ska kunna sluta sig till information kan man identifiera uppsättningen av accepterade argument, respektive $Cr_{\sigma }(S)$ uppsättningen av argument som godtroget accepteras under den semantiska $\sigma$ , och $Sc_{\sigma }(S)$ uppsättningen argument som accepteras skeptiskt under den semantiska $\sigma$ (den $\sigma$ kan vara missas om det inte finns någon möjlig tvetydighet om det semantiska).

Naturligtvis, när det bara finns en förlängning (till exempel när systemet är välgrundat), är detta problem mycket enkelt: agenten accepterar argument för den unika tillägget och avvisar andra.

Samma resonemang kan göras med märkningar som motsvarar den valda semantiken: ett argument kan accepteras om det är inne för varje märkning och vägras om det är ute för varje märkning, de andra är i ett obestämt tillstånd (argumentens status kan påminna de epistemiska tillstånden om en tro på AGM-ramverket för dynamik i övertygelser).

Likvärdighet mellan argumentationsramar

Det finns flera kriterier för likvärdighet mellan argumentationsramverk. De flesta av dessa kriterier gäller uppsättningarna av förlängningar eller uppsättningen av accepterade argument. Formellt, givet en semantisk $\sigma$ :

• ${\mathit {EQ_{1}}}$ : två argumentationsramverk är ekvivalenta om de har samma uppsättning $\sigma$ -tillägg, det vill säga $S_{1}\equiv _{1}S_{2}\Leftrightarrow Ext_{\sigma }(S_{1})=Ext_{\ sigma }(S_{2})$ ;
• ${\mathit {EQ_{2}}}$ : två argumentationsramverk är likvärdiga om de skeptiskt accepterar samma argument, det vill säga $S_{1}\equiv _{2}S_{2}\Leftrightarrow Sc_{\sigma }(S_{1})=Sc_{\sigma }(S_{2})$ ;
• ${\mathit {EQ_{2}}}$ : två argumentationsramverk är likvärdiga om de godtogsamt accepterar samma argument, det vill säga $S_{1}\equiv _{3}S_{2}\Leftrightarrow Cr_{\sigma }(S_{1})=Cr_{\sigma }(S_{2})$ .

Den starka ekvivalensen säger att två system $S_{1}$ och $S_{2}$ är ekvivalenta om och endast om för alla andra system $S_{3}$ , förening av $S_{1}$ med $S_{3}$ är ekvivalent (för ett givet kriterium) med föreningen av $S_{2}$ och ${\ displaystyle S_{3}}$ .

Andra sorter

Den abstrakta ramen för Dung har instansierats till flera särskilda fall.

Logikbaserade argumentationsramar

När det gäller logikbaserade argumentationsramar är ett argument inte en abstrakt enhet, utan ett par, där den första delen är en minimal konsistent uppsättning formler tillräckligt för att bevisa formeln för den andra delen av argumentet. Formellt är ett argument ett par $(\Phi ,\alpha )$ så att

• $\Phi \nvdash \bot$
• $\Phi \vdash \alpha$
• $\Phi$ är en minimal uppsättning av $\Delta$ som uppfyller $\alpha$ där $\Delta$ är en uppsättning formler som används av agenten för att resonera.

Man kallar $\alpha$ en konsekvens av $\Phi$ , och $\Phi$ ett stöd för $\alpha$ .

I det här fallet ges attackrelationen inte på ett explicit sätt, som en delmängd av den kartesiska produkten ${\displaystyle A\times A} ,$ utan som en egenskap som indikerar om ett argument attackerar ett annat. Till exempel,

• Relationsbesegrare : $(\Psi ,\beta )$ attacker $(\Phi ,\alpha )$ om och endast om $\beta \vdash \neg (\phi _{1}\wedge \dots \wedge \phi _{n})$ för $\{\ phi _{1},\dots ,\phi _{n}\}\subseteq \Phi$
• Relation undercut : $(\Psi ,\beta )$ attacker $(\Phi ,\alpha )$ om och endast om $\beta =\neg (\phi _{1}\wedge \dots \wedge \phi _{n})$ för $\{\phi _{1},\dots ,\phi _{n}\}\subseteq \Phi$
• Relationsbevisning : $(\Psi ,\beta )$ attacker $(\Phi ,\alpha )$ om och endast om $\beta \ Vänster högerpil \neg \alpha$ är en tautologi

Givet en viss attackrelation kan man bygga en graf och resonera på ett liknande sätt som de abstrakta argumentationsramarna (användning av semantik för att bygga utvidgning, skeptisk eller godtrogen slutledning), skillnaden är att informationen som härleds från ett logikbaserat argumentationsramverk är en uppsättning formler (konsekvenserna av de accepterade argumenten).

Värdebaserade argumentationsramar

De värdebaserade argumentationsramarna kommer från idén att under ett utbyte av argument kan vissa vara starkare än andra med avseende på ett visst värde de för fram, och så framgången för en attack mellan argument beror på skillnaden mellan dessa värden.

Formellt är ett värdebaserat argumentationsramverk en tuppel $VAF=\langle A,R,V,{\textit {val}},{\textit {valprefs}}\rangle$ med $A$ och $R$ som liknar standardramverket (en uppsättning argument och en binär relation på denna uppsättning), $V$ är en icke tom uppsättning värden, ${\textit {val}}$ är en mappning som associerar varje element från $A$ till ett element från $V$ och ${\textit { valprefs}}$ är en preferensrelation (transitiv, irreflexiv och asymmetrisk) på $V\times V$ .

besegrar ett argument ${\displaystyle a} ett annat argument$$b$ om och endast om

• $a$ attackerar $b$ i "standard" som betyder: $(a,b)\in R$ ;
• och ${\displaystyle ({\textit {val}}(b),val(a))\inte \in {\textit {valprefs}}} ,$ att är värdet som avancerats av $b$ föredras inte framför det som avancerats av $a$ .

Man påpekar att en attack lyckas om båda argumenten är associerade till samma värde, eller om det inte finns någon preferens mellan deras respektive värden.

Antagandebaserade argumentationsramar

I ramverk för antagandebaserad argumentation (ABA) definieras argument som en uppsättning regler och attacker definieras i termer av antaganden och motsatser.

Formellt är ett antagande-baserat argumentationsramverk en tuppel $\langle {\mathcal {L}},{\mathcal {R}},{\mathcal {A}}, {\overline {\mathrm {\textvisiblespace} }}\rangle$ , där

• $\langle {\mathcal {L}},{\mathcal {R}}\rangle$ är ett deduktivt system, där ${\mathcal {L}}$ är språket och ${\mathcal {R}}$ är uppsättningen av slutledningsregler i form av $s_{0}\leftarrow s_{1},\dotsc ,s_{ m}$ , för $m>0$ och $s_{0},s_{1},\dotsc ,s_{m}\in {\ mathcal {L}}$ ;
• ${\mathcal {A}}$ , där ${\mathcal {A}}\subseteq {\mathcal {L}}$ är en icke-tom mängd, benämnd antagandena ;
• ${\overline {\mathrm {\textvisiblespace} }}$ är en total mappning från ${\mathcal {A}}$ till ${\mathcal {L}}$ , där ${\overline {a}}$ definieras som motsatsen till $a$ .

Som en konsekvens av att definiera en ABA kan ett argument representeras i en trädform . Formellt, givet ett deduktivt system $\langle {\mathcal {L}},{\mathcal {R}}\rangle$ och uppsättning antaganden ${\mathcal {A} }\subseteq {\mathcal {L}}$ , ett argument för påstående ${\textstyle c\in {\mathcal {L}}}$ stöds av $S\subseteq {\mathcal {A} }$ , är ett träd med noder märkta med meningar i ${\mathcal {L}}$ eller med symbolen $\tau$ , så att:

• Roten är märkt med $c$
• För varje nod $N$ ,
  • Om $N$ är en lövnod märks $N$ antingen med ett antagande eller med $\tau$
  • Om $N$ inte är en lövnod, så finns det en inferensregel ${\displaystyle l_{N}\leftarrow s_{1},...,s_{m}} ,$ ( $\displaystyle (m\geq 0)}$ , där $l_{ N}$ är etiketten för $N$ och
    • Om $m=0$ , så ska regeln vara $l_{N}\leftarrow \tau$ (dvs underordnad av $N$ är $\tau$ )
    • Annars har $N$$m$ barn, märkta med $s_{1},...,s_{m}$
• $S$ är uppsättningen av alla antaganden som betecknar ledighetsnoderna

Ett argument med krav $c$ som stöds av en uppsättning antaganden $S$ kan också betecknas som $S\vdash c$

Se även

• Argument karta
• Argumentationsteori
• Besegrare
• Diagrammatiskt resonemang
• Dialogisk logik
• Logik och dialektik
• Argumentationens logik
• Kunskapsrepresentation och resonemang
• Parakonsekvent logik
• Probabilistisk argumentation

Anteckningar

• Trevor Bench-Capon (2002). "Värdebaserade argumentationsramar". 9:e internationella workshopen om icke-monotona resonemang (NMR 2002) : 443–454.
• Philippe Besnard; Anthony Hunter (2001). "En logikbaserad teori om deduktiva argument" . Artificiell intelligens . 128 (1–2): 203–235. doi : 10.1016/s0004-3702(01)00071-6 .
• Philippe Besnard; Anthony Hunter (2008). MIT Press (red.). Element av argumentation . Michigans universitet.
• Martin Caminada (2006). "Om frågan om återinförande i argumentation". JELIA : 111–123.
• Martin Caminada (2007). Jämföra två unika förlängningssemantik för formell argumentation: idealisk och ivrig . 19:e belgisk-nederländska konferensen om artificiell intelligens (BNAIC 2007).
• Phan Minh Dung (1995). "Om acceptansen av argument och dess grundläggande roll i icke-monotona resonemang, logikprogrammering och n-personspel. " Artificiell intelligens . 77 (2): 321–357. doi : 10.1016/0004-3702(94)00041-X .
• Phan Minh Dung; Paolo Mancarella; Francesca Toni (2006). "Datorideal skeptisk argumentation". Teknisk rapport .
• Peter Gärdenfors (1988). MIT Press (red.). Knowledge in Flux: Modeling the Dynamics of Epistemic States . Cambridge.
• Emilia Oikarinen; Stefan Woltran (2001). "Karakteriserande stark likvärdighet för argumentationsramar" . Artificiell intelligens . 175 (14–15): 1985–2009. doi : 10.1016/j.artint.2011.06.003 .
• Iyad Rahwan; Guillermo R. Simari (2009). Springer (red.). Argumentation i artificiell intelligens . Dordrecht. Bibcode : 2009aai..bok.....S .
• David S. Touretzky; John F. Horty; Richmond H. Thomason (1987). Proceedings IJCAI 1987 (red.). A Clash of Intuitions: The Current State of Nonmonotonic Multiple Inheritance Systems (PDF) . s. 476–482. Arkiverad från originalet (PDF) 2014-08-06.