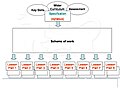
Arbetsschema

Ett arbetsschema definierar strukturen och innehållet i en akademisk kurs. Den delar upp en ofta flerårig läroplan i levererade arbetsenheter, var och en av mycket kortare veckors varaktighet (t.ex. två eller tre veckor). Varje arbetsenhet analyseras sedan ut till inlärbara individuella ämnen av ännu kortare varaktighet (t.ex. två timmar eller mindre).

Bättre arbetsscheman kartlägger tydligt hur resurser (t.ex. böcker, utrustning, tid) och klassaktiviteter (t.ex. lärarsamtal, grupparbeten, övningar, diskussioner) och bedömningsstrategier (t.ex. prov , frågesporter, frågor och svar, läxor ) kommer att användas för att lära ut varje ämne och bedöma elevernas framsteg när det gäller att lära sig det material som hör samman med varje ämne, enhet och arbetsschemat som helhet. När eleverna går vidare genom arbetsschemat, finns det en förväntning om att deras uppfattning om kopplingarna mellan ämnen och enheter kommer att förbättras.

Arbetsscheman kan innehålla tider och datum (deadlines) för att leverera de olika delarna av läroplanen. Filosofiskt är detta kopplat till en övertygelse om att alla elever bör exponeras för alla delar av läroplanen så att de som kan "hänga med" ("den bästa"/eliten) inte går miste om något innehåll och kan uppnå högsta betyg. Detta kan beskrivas som en "traditionalistisk" syn.

Det finns en motstridig filosofisk syn på att deadlines bör undvikas och att varje klass ska utvecklas i sin egen takt: så att ingen elev blir "lämnad". Medan de återstående eleverna "kommer ikapp", bör de elever som förstår snabbt placeras i ett "hållningsmönster" fullt av pussel och frågor som utmanar dem att koppla ihop det senaste lärandet med mer etablerat lärande (de kan också uppmuntras att spendera en liten tid för att förbättra deras förståelse genom att stödja lärare i att ta bort underliggande fel/frågor från medstudenter som inte har fattat de senaste idéerna lika snabbt). Denna uppfattning kan beskrivas som ett "mästerskapssätt". I matematikundervisningen i England stöds det starkt av det statligt finansierade National Center for Excellence in Teaching Mathematics baserat på forskning som vägleds av skolors globalt exceptionella prestanda i Singapore och Shanghai.

Läroplan

Arbetsschemat är vanligtvis en tolkning av en specifikation eller kursplan och kan användas som vägledning under hela kursen för att övervaka framstegen mot den ursprungliga planen. Arbetsscheman kan delas med eleverna så att de har en överblick över sin kurs.

Den ultimata källan till specifikationen eller kursplanen är en läroplan. Läroplaner definieras vanligtvis av regeringen och därmed av lagar och/eller förordningar. Följaktligen har varje land sina egna (även om vissa länder väljer att anta läroplaner som definieras av andra länder).

För att skapa ett arbetsschema är det viktigt att ha detaljerad hänsyn till den lagstadgade läroplanen i det land där arbetsschemat ska levereras. Dessa definieras vanligtvis i detalj efter ämne. Att förstå subtiliteterna och nyanserna i deras presentation är av avgörande betydelse när man definierar de mest användbara arbetsscheman.

England

För underhållna skolor och examensnämnder i England är den nationella läroplanen fastställd av Department for Education så att alla barn som växer upp i England har en i stort sett liknande utbildning.

Läroplanen för primärutbildning (åldrar 4/5 till 11) och gymnasieutbildning (åldrar 11 till 18) i England är uppdelad i fem nyckelstadier. Nyckelsteg 1 och 2 levereras på grundskolor. Nyckelsteg 3, 4 och 5 levereras på gymnasieskolor.

England - Matematik

Engelska grundskolor: nyckelstadier 1 och 2 [åldrar 5 till 11]

Förväntningarna på att leverera den nationella läroplanen för matematik i England vid nyckelstadierna 1 och 2 är noggrant definierade med tydliga tidsbundna mål. Utbildningsdepartementet har tillhandahållit ett första årligt arbetsschema (eller uppsättning förväntningar) för varje skola/läsår från år 1 (ålder 5/6) till och med år 6 (ålder 10/11). Detta specificerar inte ordningen för undervisningen för varje ämne inom varje år; men ger vägledning och anger förväntningarna på vad som ska läras ut och läras i slutet av varje år av elevernas grundskoleutbildning.

Engelska gymnasieskolor: nyckelstadier 3 och 4 [åldrar 11 till 16]

Den nationella läroplanen för matematik i England är också hårt definierad på nyckelstadierna 3 och 4. Varje enskild engelsk skolas matematiska avdelning ges dock större frihet att bestämma när och hur innehållet ska levereras. Till skillnad från den nationella läroplanen för Englands grundskolor finns det inga årliga förväntningar. Istället sätts vägledningen med hänvisning till vad som ska läras ut och läras i slutet av nyckelsteg 3 [slutet av år 9 (ålder 13/14)] och i slutet av nyckelsteg 4 [slutet av år 11 ( åldrarna 15/16)].

Det är anmärkningsvärt att läroplanen för Key Stage 4 är avsedd av Department for Education att undersöka allt lärande från Key Stage 1 till 4. I synnerhet är ämnen som anges i Key Stage 3 uttryckligen en del av läroplanen för Key Stage 4 (såsom att grunderna för tidigare lärande stärks samtidigt som man bygger vidare på dem). Följaktligen får elever som har kämpat med de svårare att förstå delarna tidigare möjligheten att bemästra innehållet i Key Stage 3 medan andra bygger högre parallellt.

Engelska gymnasieskolor: GCSEs [vanligen ålder 15/16+]

Det är obligatoriskt i England för elever att ha tagit en GCSE i matematik senast det år de fyller sexton år.

Det är anmärkningsvärt att ämnesinnehållet som avtalats mellan Department of Education och The Office of Qualifications and Examination Regulation (Ofqual) [examensnämndens regulator för GCSEs, AS-Levels och A-Levels] framhävs på subtilt olika sätt än ämnesinnehållet av den nationella läroplanen för nyckelsteg 4.

Den senare har två nivåer av förväntningar (oformaterad text kontra {fet stil och 'parenteser'}) ; den förra har tre (oformaterad text, understruken text och fet text ). Den subtila distinktionen gjorde det möjligt för mer insiktsfulla elever, föräldrar och pedagoger att bestämma (eller spekulera om) hur innehåll är (eller bör fördelas) mellan de två olika uppsättningarna av GCSE matematikundersökningar (grund och högre): dessa två uppsättningar överlappning (som tyder på att de understrukna ämnena finns i skärningspunkten mellan de två uppsättningarna av ämnen).

Det är också anmärkningsvärt att läroplanen för GCSE är avsedd av Department for Education att undersöka allt lärande från nyckelstadier 1 till 4. I synnerhet är ämnen listade i nyckelsteg 3 uttryckligen en del av läroplanen för nyckelstadie 4 och GCSE ( så att grunderna för tidigare lärande stärks samtidigt som man bygger vidare på dem). Följaktligen får elever som har kämpat med de svårare att förstå delarna tidigare möjligheten att bemästra innehållet i Key Stage 3 medan andra bygger högre parallellt.

Engelska gymnasieskolor: AS och A-nivåer [vanligtvis ålder 17+]

AS och A-nivåer i matematik är inte obligatoriska.

Följaktligen finns det ingen nationell läroplan för AS och A-Level matematik i England. Det finns dock överenskommet ämnesinnehåll som krävs av Institutionen för utbildning för AS- och A-nivåspecifikationer i matematik.

Element

De viktigaste delarna av ett "arbete" kan inkludera:

Innehåll 1

Mål eller resultat

Leveranssätt (student- och lärareaktivitet)

Bedömningsstrategier

Resurser

Övrigt Anmärkningar

• 

  arbetsschema

Exempel på ett enkelt arbetsschema

Se även Lektionsplaner .

Arbetsscheman [1]