Översamplad binär bildsensor

En översamplad binär bildsensor är en bildsensor med icke-linjär respons som påminner om traditionell fotografisk film . Varje pixel i sensorn har ett binärt svar, vilket endast ger en enbits kvantifierad mätning av den lokala ljusintensiteten. Bildsensorns svarsfunktion är icke-linjär och liknar en logaritmisk funktion, vilket gör sensorn lämplig för avbildning med högt dynamiskt omfång .

Arbetsprincip

Före tillkomsten av digitala bildsensorer använde fotografi, under större delen av sin historia, film för att registrera ljusinformation. I hjärtat av varje fotografisk film finns ett stort antal ljuskänsliga korn av silverhalogenidkristaller . Under exponeringen har varje mikronstort korn ett binärt öde: Antingen träffas det av några infallande fotoner och blir "exponerat", eller så missas det av fotonbombardementet och förblir "oexponerat". I den efterföljande filmutvecklingsprocessen omvandlas exponerade korn, på grund av deras förändrade kemiska egenskaper, till silvermetall, vilket bidrar till ogenomskinliga fläckar på filmen; oexponerade korn tvättas bort i ett kemiskt bad och lämnar kvar de genomskinliga områdena på filmen. Sålunda är fotografisk film i huvudsak ett binärt avbildningsmedium, som använder lokala densiteter av ogenomskinliga silverkorn för att koda den ursprungliga ljusintensitetsinformationen. Tack vare den lilla storleken och det stora antalet av dessa korn, märker man knappt denna kvantiserade karaktär av filmen när man tittar på den på avstånd, och observerar bara en kontinuerlig grå ton.

Den översamplade binära bildsensorn påminner om fotografisk film. Varje pixel i sensorn har ett binärt svar, vilket endast ger en enbits kvantifierad mätning av den lokala ljusintensiteten. I början av exponeringsperioden sätts alla pixlar till 0. En pixel sätts sedan till 1 om antalet fotoner som når den under exponeringen är minst lika med en given tröskel q . Ett sätt att bygga sådana binära sensorer är att modifiera standardminneschipteknologi, där varje minnesbitcell är designad för att vara känslig för synligt ljus. Med nuvarande CMOS-teknik kan integrationsnivån för sådana system överstiga 10 ⁹ ~ 10 ¹⁰ (dvs. 1 giga till 10 giga) pixlar per chip. I det här fallet är motsvarande pixelstorlekar (cirka 50~nm) långt under ljusets diffraktionsgräns, och bildsensorn översamplar således ljusfältets optiska upplösning. Intuitivt kan man utnyttja denna rumsliga redundans för att kompensera för informationsförlusten på grund av enbits kvantiseringar, vilket är klassiskt vid översampling av delta-sigma-konverteringar.

Att bygga en binär sensor som emulerar den fotografiska filmprocessen föreställdes först av Fossum , som myntade namnet digital filmsensor (nu kallad en kvantabildsensor ). Den ursprungliga motiveringen var huvudsakligen av teknisk nödvändighet. Miniatyriseringen av kamerasystem kräver en kontinuerlig krympning av pixelstorlekar . Vid en viss punkt blir dock den begränsade fullbrunnskapaciteten (dvs. de maximala fotonelektronerna en pixel kan hålla) för små pixlar en flaskhals, vilket ger mycket låga signal-brus- förhållanden (SNR) och dåliga dynamiska intervall . Däremot har en binär sensor vars pixlar bara behöver detektera ett fåtal fotonelektroner runt ett litet tröskelvärde q mycket mindre krav på fullbrunnskapacitet, vilket gör att pixelstorlekarna kan krympa ytterligare.

Bildmodell

Linsen

Fig.1 Bildmodellen. Den förenklade arkitekturen för ett diffraktionsbegränsat bildsystem. Infallande ljusfält $\lambda _{0}(x)$ passerar genom en optisk lins, som fungerar som ett linjärt system med en diffraktionsbegränsad punktspridningsfunktion (PSF). Resultatet är ett utjämnat ljusfält ${\displaystyle \lambda (x)} ,$ som sedan fångas av bildsensorn.

Tänk på en förenklad kameramodell som visas i Fig.1. λ $\displaystyle \lambda _{0}(x)}$ är fältet för inkommande ljusintensitet. Genom att anta att ljusintensiteterna förblir konstanta inom en kort exponeringsperiod kan fältet modelleras endast som en funktion av den rumsliga variabeln $x$ . Efter att ha passerat genom det optiska systemet , filtreras det ursprungliga ljusfältet ${\displaystyle \lambda _{0}(x)} av linsen, som fungerar som ett linjärt system med ett givet impulssvar.$ På grund av ofullkomligheter (t.ex. aberrationer) i linsen kan impulssvaret, alias punktspridningsfunktionen ( PSF) för det optiska systemet, inte vara ett Dirac-delta, vilket innebär en gräns för upplösningen av det observerbara ljusfältet. En mer fundamental fysisk gräns beror dock på ljusdiffraktion . Som ett resultat, även om objektivet är idealiskt, är PSF fortfarande oundvikligen en liten suddig fläck. Inom optik kallas en sådan diffraktionsbegränsad punkt ofta för Airy disk , vars radie $\displaystyle R_{a}}$ kan beräknas som

${\displaystyle R_{a}=1,22\,wf,$

där $w$ är ljusets våglängd och $f$ är F-numret för det optiska systemet. På grund av lågpass (utjämnande) natur, har den resulterande $\lambda (x)$ en ändlig rumslig upplösning, dvs den har ett ändligt antal frihetsgrader per rymdenhet.

Sensorn

Fig.2 Modellen för den binära bildsensorn. Pixlarna (visade som "buckets") samlar in fotoner, vars antal jämförs med en kvantiseringströskel q . I figuren illustrerar vi fallet när q = 2. Pixelutgångarna är binära: $b_{m}=1$ (dvs vita pixlar) om det finns minst två fotoner som tas emot av pixeln ; annars, $b_{m}=0$ (dvs. grå pixlar).

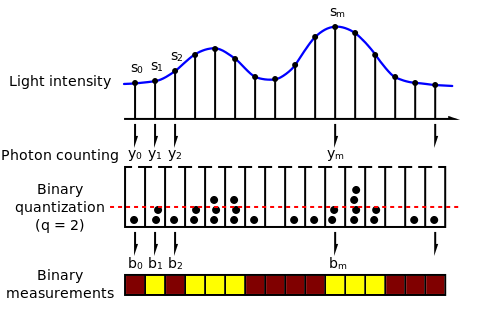
Fig. 2 illustrerar den binära sensormodellen. s $s_{m}$ anger exponeringsvärdena som ackumuleras av sensorpixlarna Beroende på de lokala värdena för $s_{m}$ samlar varje pixel (avbildad som "hinkar" i figuren) ett annat antal fotoner som träffar dess yta. $y_{m}$ är antalet fotoner som träffar ytan av den ${\displaystyle m}:$ te pixeln under en exponeringsperiod . Relationen mellan $s_{m}$ och fotonantalet $y_{m}$ är stokastisk. Mer specifikt $y_{m}$ modelleras som realiseringar av en Poisson-slumpvariabel, vars intensitetsparameter är lika med $s_{m}$ ,

Som en ljuskänslig enhet omvandlar varje pixel i bildsensorn fotoner till elektriska signaler, vars amplitud är proportionell mot antalet fotoner som träffar den pixeln. I en konventionell sensordesign kvantiseras sedan de analoga elektriska signalerna av en A/D-omvandlare till 8 till 14 bitar (vanligtvis ju fler bitar desto bättre). Men i den binära sensorn är kvantiseraren 1 bit. I fig. 2 $b_{m}$ den kvantiserade utsignalen från den ${\displaystyle m}:$ te pixeln. Eftersom fotontalet $y_{m}$ dras från slumpvariabler, så är det även den binära sensorns utsignal $b_{m}$ .

Rumslig och tidsmässig översampling

Om det är tillåtet att ha temporal översampling, dvs att ta flera på varandra följande och oberoende bildrutor utan att ändra den totala exponeringstiden ${\displaystyle \tau },$ är prestandan för den binära sensorn likvärdig med sensorn med samma antal rumsliga översamplingar under vissa skick. Det betyder att människor kan göra avvägningar mellan rumslig översampling och tidsmässig översampling. Detta är ganska viktigt, eftersom tekniken vanligtvis ger begränsningar på storleken på pixlarna och exponeringstiden.

Fördelar jämfört med traditionella sensorer

På grund av den begränsade fullbrunnskapaciteten hos konventionella bildpixlar kommer pixeln att mättas när ljusintensiteten är för stark. Detta är anledningen till att pixelns dynamiska omfång är lågt. För den översamplade binära bildsensorn är det dynamiska området inte definierat för en enda pixel, utan en grupp av pixlar, vilket gör det dynamiska området högt.

Rekonstruktion

Fig.4 Rekonstruera en bild från de binära mätningarna tagna av en SPAD-sensor, med en rumslig upplösning på 32×32 pixlar. Den slutliga bilden (nedre högra hörnet) erhålls genom att införliva 4096 på varandra följande ramar, varav 11 visas i figuren.

En av de viktigaste utmaningarna med användningen av en översamplad binär bildsensor är rekonstruktionen av ljusintensiteten $\lambda (x)$ från det binära måttet $b_{m}$ . Maximal sannolikhetsuppskattning kan användas för att lösa detta problem. Fig. 4 visar resultaten av att rekonstruera ljusintensiteten från 4 096 binära bilder tagna med enkelfoton lavindioder ( SPADs) kamera. En bättre rekonstruktionskvalitet med färre tidsmätningar och snabbare, hårdvaruvänlig implementering kan uppnås med mer sofistikerade algoritmer.