Voigt effekt

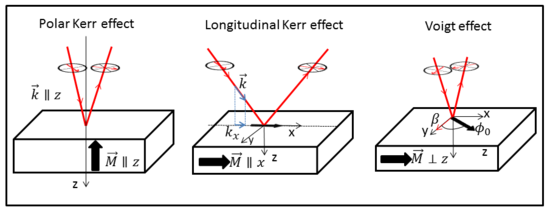
Schematisk över den polära Kerr-effekten, longitudinella Kerr-effekten och Voigt-effekten

Voigt -effekten är ett magneto-optiskt fenomen som roterar och elliptiserar linjärt polariserat ljus som skickas in i ett optiskt aktivt medium. Till skillnad från många andra magnetoptiska effekter som Kerr- eller Faraday-effekten som är linjärt proportionella mot magnetiseringen (eller mot det applicerade magnetfältet för ett icke magnetiserat material), är Voigt-effekten proportionell mot kvadraten på magnetiseringen (eller kvadraten på magnetiseringen). magnetfältet ) och kan ses experimentellt vid normal incidens . Det finns flera valörer för denna effekt i litteraturen: Cotton-Mouton-effekten (med hänvisning till de franska forskarna Aimé Cotton och Henri Mouton ), Voigt-effekten (med hänvisning till den tyske vetenskapsmannen Woldemar Voigt ) och magnetisk-linjär dubbelbrytning . Denna sista valör är närmare i fysisk mening, där Voigt-effekten är en magnetisk dubbelbrytning av materialet med ett brytningsindex parallellt ( $n_{\parallel }$ ) och vinkelrät $(n_) {\perp }$ ) till magnetiseringsvektorn eller till det applicerade magnetfältet.

För en elektromagnetisk infallande våg linjärt polariserad ${\displaystyle {\vec {E_{i}}}=(\ cos \beta ,\,\sin \beta ,\,0)e^{-i\omega (t-n_{1}z/c)}} och ett polariserat$ sampel i planet ${\displaystyle {\vec {m}}=(\cos \phi ,\,\sin \phi ,\,0)} , uttrycket$ för rotationen i reflektionsgeometrin är $\ delta \beta$ är:

$$\delta \beta _{r}={\frac {2\Delta n}{n_{0}^{2 }-1}}\sin[2(\phi -\beta )]$$

och i transmissionsgeometrin:

$$\delta \beta _{t} ={\frac {B_{1}+n_{0}^{2}{\Big [}{\frac {2L\omega }{c}}(1+n_{0})Q_{i}Q_{r }+Q_{r}^{2}-Q_{i}^{2}{\Big ]}}{n_{0}(1+n_{0})}},$$

där ${\textstyle \Delta n={\frac {n_{\parallel }-n_{\perp }}{2}}} är skillnaden$ mellan brytningsindex beroende på Voigt-parametern $Q=Q_{i}+iQ_{r}$ (samma som för Kerr-effekten), $n_{0}$ materialbrytningsindexen och $B_{1}$ parametern som är ansvarig för Voigt-effekten och så proportionell mot $M^{2}$ eller $(\mu _{0}H)^{2}$ i fallet med ett paramagnetiskt material.

Detaljerad beräkning och en illustration ges i avsnitten nedan.

Teori

Ram och koordinatsystem för härledning av Voigt-effekt. ${\vec {E}}_{i}$ , ${\vec {E}}_{r}$ och ${\vec {E} }_{t}$ syftar på det infallande, reflekterade och överförda elektromagnetiska fältet.

Liksom med de andra magnetoptiska effekterna utvecklas teorin på ett standard sätt med användning av en effektiv dielektrisk tensor från vilken man beräknar systemegenvärden och egenvektorer. Som vanligt, från denna tensor, beskrivs magneto-optiska fenomen huvudsakligen av de off-diagonala elementen.

Här betraktar man en infallande polarisation som fortplantar sig i z-riktningen: ${\displaystyle {\vec {E_{i }}}=(\cos \beta ,\,\sin \beta ,\,0)e^{-i\omega (t-n_{1}z/c)}} det elektriska fältet och ett homogent i-$ plan magnetiserat prov ${\displaystyle {\vec {m}}=(\cos \phi ,\,\sin \phi ,\,0)} där$ ϕ $\displaystyle \ phi }$ räknas från den [100] kristallografiska riktningen. Målet är att beräkna ${\vec {E_{r}} }=(\cos \beta +\delta \beta ,\,\sin \beta +\delta \beta ,\,0)e^{-i\omega (t+n_{1}z/c)}$ där $\delta \beta$ är rotationen av polarisationen på grund av kopplingen mellan ljuset och magnetiseringen. Låt oss lägga märke till att $\delta \beta$ experimentellt är en liten kvantitet av storleksordningen mrad. ${\vec {m}}$ är den reducerade magnetiseringsvektorn definierad av ${\vec {m}}={\vec {M}}/M_{s }$ , $M_{s}$ magnetiseringen vid mättnad. Vi betonade med det faktum att det är för att ljusutbredningsvektorn är vinkelrät mot magnetiseringsplanet som det är möjligt att se Voigt-effekten.

Dielektrisk tensor

Efter notationen av Hubert tar den generaliserade dielektriska kubiska tensorn $\varepsilon _{r}$ följande form:

$$(1)\qquad \varepsilon _{r}=\epsilon {\begin{bmatrix}1&0&iQm_{y}\\0&1&-iQm_{x}\\-iQm_{ y}&iQm_{x}&1\end{bmatrix}}+{\begin{bmatrix}B_{1}m_{x}^{2}&B_{2}m_{x}m_{y}&0\\B_{2 }m_{x}m_{y}&B_{1}m_{y}^{2}&0\\0&0&B_{1}m_{z}^{2}\end{bmatrix}}$$

där $\varepsilon$ är materialets dielektriska konstant, $Q$ Voigt-parametern, $B_{1}$ och $B_{2}$ två kubikkonstanter som beskriver magneto -optisk effekt beroende på $m_{i}^{2}$ . $m_{i}$ är reduceringen $m_{i}=M_{i}/M_{s}$ . Beräkningen görs i den sfäriska approximationen med $B_{1}=B_{2}$ . För närvarande, det finns inga bevis för att denna approximation inte är giltig, eftersom observationen av Voigt-effekten är sällsynt eftersom den är extremt liten med avseende på Kerr-effekten.

Egenvärden och egenvektorer

För att beräkna egenvärdena och egenvektorerna betraktar vi utbredningsekvationen som härleds från Maxwells ekvationer, med konventionen ${\vec {n}}={\vec {k}}c/\ omega$ :

$$(2)\qquad n^{2}{\vec {E}}-{\vec {n}}( {\vec {n}}\cdot {\vec {E}})=\varepsilon {\vec {E}}$$

När magnetiseringen är vinkelrät mot utbredningsvågvektorn, i motsats till Kerr-effekten, kan ${\displaystyle {\vec {E}}} ha alla sina tre komponenter lika med noll vilket gör beräkningarna mer komplicerade och gör Fresnels ekvationer nej$ längre giltig. Ett sätt att förenkla problemet består i att använda den elektriska fältförskjutningsvektorn ${\vec {D}}=\varepsilon {\vec {E}}$ . Eftersom ${\vec {\nabla }}\cdot {\vec {D}}=0$ och ${\vec {k}}\parallel {\ vec {z}}$ vi har ${\vec {D}}=(D_{x},D_{y},0)$ . Det obekväma är att hantera den omvända dielektriska tensorn som kan vara komplicerad att hantera. Här görs beräkningar i det allmänna fallet som är komplicerat matematiskt att hantera, men man kan enkelt följa demonstrationen genom att betrakta $\phi =0$ .

Egenvärden och egenvektorer hittas genom att lösa fortplantningsekvationen på ${\vec {D}}$ som ger följande ekvationssystem:

$${\ displaystyle (3)\quad {\begin{cases}(\varepsilon _{xx}^{-1}-{\frac {1}{n^{2}}})D_{x}+\epsilon _{xy }^{-1}D_{y}=0\\\\\varepsilon _{yx}^{-1}D_{x}+(\varepsilon _{yy}^{-1}-{\frac {1 }{n^{2}}})D_{y}=0\end{cases}}}$$

där $\varepsilon _{ij}^{-1}$ representerar det inversa $ij$ -elementet av den dielektriska tensorn $\varepsilon _{r}$ , och $n^{2}=\varepsilon$ . Efter en enkel beräkning av systemets determinant måste man göra ett utvecklingssteg på 2:a ordningen i $Q$ och första ordningen av $B_{1}$ . Detta ledde till de två egenvärdena som motsvarar de två brytningsindexen:

$$n_{\parallel }^{2}=\varepsilon +B_{1}$$

$$n_{\perp }^{2}=\varepsilon (1-Q^{2})$$

Motsvarande egenvektorer för ${\vec {D}}$ och för ${\vec {E}}$ är:

$$(4)\qquad {\vec {D}}_{\parallel }={\begin{pmatrix}\cos(\phi )\\\ sin(\phi )\\0\end{pmatrix}}\qquad {\vec {D}}_{\perp }={\begin{pmatrix}-\sin(\phi )\\\cos(\phi ) \\0\end{pmatrix}}\qquad {\vec {E}}_{\parallel }=\varepsilon ^{-1}{\vec {D}}_{\parallel }={\begin{pmatrix} {\frac {\cos(\phi )}{B_{1}+\varepsilon }}\\{\frac {\sin(\phi )}{B_{1}+\epsilon }}\\0\end{ pmatrix}}\qquad {\vec {E}}_{\perp }=\varepsilon ^{-1}{\vec {D}}_{\perp }={\begin{pmatrix}{\frac {\sin (\phi )}{(Q^{2}-1)\epsilon }}\\{\frac {\cos(\phi )}{(1-Q^{2})\epsilon }}\\{\ frac {-iQ}{(1-Q^{2})\epsilon }}\end{pmatrix}}$$

Reflexionsgeometri

Kontinuitetsrelation

Genom att känna till egenvektorerna och egenvärdena inuti materialet måste man beräkna ${\vec {E_{r}}}=(E_{rx},E_{ry },0)$ den reflekterade elektromagnetiska vektorn som vanligtvis detekteras i experiment. Vi använder kontinuitetsekvationerna för ${\vec {E}}$ och ${\vec {H}}$ där ${\vec {H}}$ är induktionen definieras från Maxwells ekvationer av ${\textstyle {\vec {\nabla }}\times {\vec {H}}={\frac {1}{c}}{ \frac {\partial {\vec {D}}}{\partial t}}}$ . Inuti mediet bryts det elektromagnetiska fältet ned på de härledda egenvektorerna ${\vec {E}}_{t}=\alpha {\vec {E}} _{\parallel }+\beta {\vec {E}}_{\perp }$ . Ekvationssystemet att lösa är:

$$(5)\quad {\begin{cases}\alpha {\Big (}{\frac {D_{y\parallel }}{n_{\parallel }}}{\Big )}+\beta {\Big (}{\frac {D_{y\perp }}{n_ {\perp }}}{\Big )}+E_{ry}=E_{0y}\\\\\alpha {\Big (}{\frac {D_{x\parallel }}{n_{\parallel }} }{\Big )}+\beta {\Big (}{\frac {D_{x\perp }}{n_{\perp }}}{\Big )}+E_{rx}=E_{0x}\\ \\\alpha E_{x\parallel }+\beta E_{x\perp }-E_{rx}=E_{0x}\\\\\alpha E_{y\parallel }+\beta E_{y\perp } -E_{ry}=E_{0y}\end{cases}}$$

Lösningen av detta ekvationssystem är:

$$_ \displaystyle (6)\quad E_{rx}=E_{0}{\frac {(1-n_{\perp }n_{\parallel })\cos(\beta )+(n_{\perp }-n_{ \parallel })\cos(\beta -2\phi )}{(1+n_{\parallel })(1+n_{\perp })}}}$$

$$_ \displaystyle (7)\quad E_{ry}=E_{0}{\frac {(1-n_{\perp }n_{\parallel })\sin(\beta )-(n_{\perp }-n_{ \parallel })\sin(\beta -2\phi )}{(1+n_{\parallel })(1+n_{\perp })}}}$$

Beräkning av rotationsvinkel

Rotationsvinkeln $\delta \beta$ och ellipticitetsvinkeln $\psi$ definieras från förhållandet $\chi =E_{ry}/E_ {rx}$ med följande två formler:

$$(8)\quad \tan 2\delta \beta ={\frac {2\operatörsnamn {Re} (\chi )}{1-|\chi |^{2}}}\qquad (9 )\quad \sin(2\psi _{K})={\frac {2\operatörsnamn {Im} (\chi )}{1-|\chi |^{2}}},$$

där $\operatorname {Re} (\chi )$ och $\operatorname {Im} (\chi )$ representerar den verkliga och imaginära delen av $\ chi$ . Genom att använda de två tidigare beräknade komponenterna får man:

$$(10)\qquad \chi ={\frac {(B_{1}+n_{0}^{2}Q^{2})}{2n_{0}(n_{0}^{2} -1)}}{\frac {\sin[2(\phi -\beta )]}{\cos(\beta )^{2}}}+\tan(\beta ).$$

Detta ger för Voigt-rotationen:

$$(11)\qquad \delta \beta =\ operatornamn {Re} \left[{\frac {B_{1}+n_{0}^{2}Q^{2}}{2n_{0}(n_{0}^{2}-1)}}\ höger]\sin[2(\phi -\beta )],$$

som också kan skrivas om i fallet med $B_{1}$ , $n_{0}$ och $Q$ real:

$$(12)\quad \delta \beta ={\frac {2\Delta n}{n_{0 }^{2}-1}}\sin[2(\phi -\beta )],$$

där $\Delta n={\frac {n_{\parallel }-n_{\perp }}{2}}$ är skillnaden mellan brytningsindex. Följaktligen får man något som är proportionellt mot $\Delta n$ och som beror på den infallande linjära polarisationen. För korrekt $\phi -\beta$ kan ingen Voigt-rotation observeras. $\Delta n$ är proportionell mot kvadraten på magnetiseringen eftersom $B_{1}\propto M_{s}^{2}$ och $Q\propto M_{s}$ .

Transmissionsgeometri

Beräkningen av rotationen av Voigt-effekten vid överföring är i princip likvärdig med den för Faraday-effekten. I praktiken används inte denna konfiguration i allmänhet för ferromagnetiska prover eftersom absorptionslängden är svag i denna typ av material. Användningen av transmissionsgeometri är dock vanligare för paramagnetisk vätska eller kristall där ljuset lätt kan färdas in i materialet.

Beräkningen för ett paramagnetiskt material är exakt densamma med avseende på ett ferromagnetiskt, förutom att magnetiseringen ersätts av ett fält ${\displaystyle \mu _{0} {\vec {H}}=\mu _{0}H_{0}(\cos \phi ,\,\sin \phi )} (H {\displaystyle$ H_ $}$ i $\ mathrm {A/m}$ eller $\mathrm {G}$ ). För enkelhetens skull kommer fältet att läggas till i slutet av beräkningen i de magnetoptiska parametrarna.

Betrakta de utsända elektromagnetiska vågorna ${\vec {E}}_{t}$ som fortplantar sig i ett medium med längden L. Från ekvation (5) får man för $\alpha$ och ${ \displaystyle \beta }$ :

$$\alpha ={\frac {2E_{0}n_{\parallel }\cos(\theta -\phi )}{1+n_ {\parallell }}}$$

$$\beta ={\frac {2E_{0}n_{\perp }^{2}\sin(\theta -\phi ) }{n_{\perp }+1}}$$

Vid positionen z = L är uttrycket för ${\displaystyle {\vec {E}}_{t}}:$

$$(13)\quad {\vec {E}}_{t}=e^{-i\omega [t+{\frac {(n_{\parallel }+n_{\perp })L}{ 2c}}]}{\Big [}\alpha {\vec {E}}_{\parallel }e^{i{\frac {\omega \Delta nL}{c}}}+\beta {\vec { E}}_{\perp }e^{-i{\frac {\omega \Delta nL}{c}}}{\Big ]}$$

där ${\vec {E}}_{\parallel }$ och ${\vec {E}}_{\perp }$ är egenvektorerna som tidigare beräknats, och ${\displaystyle \Delta n={\frac {n_{\parallel }-n_{\perp }}{2}}} är skillnaden$ för de två brytningsindexen. Rotationen beräknas sedan från förhållandet ${\displaystyle \chi ={\frac {E_{t_{y}}}{E_{t_{x}}}}} ,$ med utveckling i första ordning i $B_{1}$ och andra ordningen i $Q$ . Detta ger:

$$(14)\quad \chi ={\frac {ci~\ omega L(1+n_{0})(B_{1}+n_{0}Q^{2})\sin[2(\beta -\phi )]}{4cn_{0}(1+n_{0 })\cos ^{2}(\beta )}}={\frac {ci~\omega L(1+n_{0})\Delta n\sin[2(\beta -\phi )]}{c ~(1+n_{0})\cos ^{2}(\beta )}}$$

Återigen får vi något proportionellt mot $\Delta n$ och $L$ , ljusets utbredningslängd. Låt oss lägga märke till att $\Delta n$ är proportionell mot $(\mu _{0}H_{0})^{2}$ på samma sätt med avseende på geometrin i reflektion för magnetiseringen. För att extrahera Voigt-rotationen betraktar vi $n_{0}=\eta +i~\kappa$ , $Q=Q_{r} +i~Q_{i}$ och $B_{1}$ verklig. Sedan måste vi beräkna den verkliga delen av (14). Det resulterande uttrycket infogas sedan i (8). I approximationen av ingen absorption får man för Voigt-rotationen i transmissionsgeometri:

$$(15 )\quad \delta \beta =(\mu _{0}H)^{2}{\frac {B_{1}+n_{0}^{2}{\Big [}{\frac {2L\omega }{c}}(1+n_{0})Q_{i}Q_{r}+Q_{r}^{2}-Q_{i}^{2}{\Big ]}}{n_{0} (1+n_{0})}}$$

Illustration av Voigt-effekten i GaMnAs

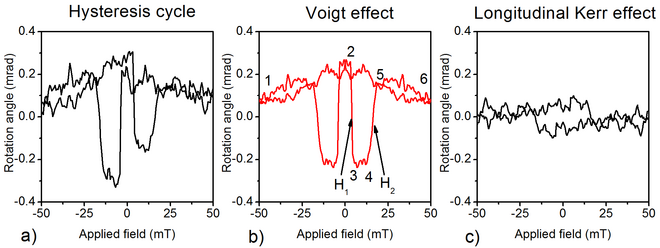
Fig 1: a) Experimentell hysterescykel på ett plant (Ga,Mn)As prov b) Voigt hysterescykel erhållen genom att extrahera den symmetriska delen av (a). c) Longitudinell Kerr erhållen genom att extrahera den asymmetriska delen av (a)

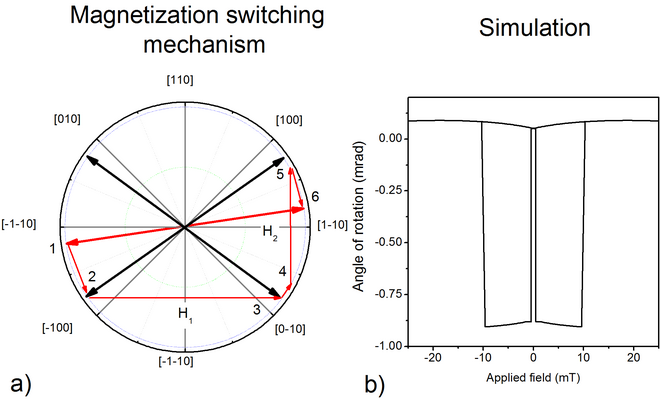
Fig 2: a) Omkopplingsmekanism för ett i planet (Ga,Mn)Som prov för ett magnetfält som appliceras längs [1-10]-axeln vid 12 K. b) Voigt-signal simulerad från mekanismen som visas i a)

Som en illustration av tillämpningen av Voigt-effekten ger vi ett exempel i den magnetiska halvledaren (Ga,Mn)As där en stor Voigt-effekt observerades. Vid låga temperaturer (i allmänhet för $T<{\frac {T_{c}}{2}}$ ) för ett material med en magnetisering i planet, uppvisar (Ga,Mn)As en biaxiell anisotropi med magnetiseringen inriktad längs (eller nära) <100> riktningar.

En typisk hysterescykel som innehåller Voigt-effekten visas i figur 1. Denna cykel erhölls genom att sända ett linjärt polariserat ljus längs [110]-riktningen med en infallsvinkel på ungefär 3° (mer information finns i ), och mäta rotation på grund av magnetoptiska effekter av den reflekterade ljusstrålen. I motsats till den vanliga longitudinella/polära Kerr-effekten är hysterescykeln jämn med avseende på magnetiseringen, vilket är en signatur för Voigt-effekten. Denna cykel erhölls med ett ljusinfall mycket nära det normala, och det uppvisar också en liten udda del; en korrekt behandling måste utföras för att extrahera den symmetriska delen av hysteresen som motsvarar Voigt-effekten och den asymmetriska delen som motsvarar den longitudinella Kerr-effekten.

I fallet med hysteresen som presenteras här applicerades fältet längs [1-10]-riktningen. Omkopplingsmekanismen är som följer:

1. Vi börjar med ett högt negativt fält och magnetiseringen är nära [-1-10] riktningen vid position 1.
2. Magnetfältet minskar vilket leder till en koherent magnetiseringsrotation från 1 till 2
3. Vid positivt fält växlar magnetiseringen brutalt från 2 till 3 genom kärnbildning och fortplantning av magnetiska domäner som ger ett första tvångsfält som här heter $H_{1}$
4. Magnetiseringen förblir nära tillståndet 3 medan den roterar koherent till tillståndet 4, närmare från den applicerade fältriktningen.
5. Återigen växlar magnetiseringen abrupt från 4 till 5 genom kärnbildning och fortplantning av magnetiska domäner. Denna omkoppling beror på det faktum att den slutliga jämviktspositionen är närmare tillståndet 5 med avseende på tillståndet 4 (och så hans magnetiska energi är lägre). Detta ger ett annat tvångsfält som heter $H_{2}$
6. Slutligen roterar magnetiseringen koherent från tillstånd 5 till tillstånd 6.

Simuleringen av detta scenario ges i figur 2, med

$$\operatorname {Re} \left[{\frac {B_{1}+n_{0}^{2}Q^{2}}{2n_{0}(n_{0}^{2}-1 )}}\right]P_{\text{Voigt}}=0.5\,\mathrm {mrad} .$$

Som man kan se är den simulerade hysteresen kvalitativt densamma med avseende på den experimentella. Lägg märke till att amplituden vid $H_{1}$ eller $H_{2}$ är ungefär två gånger av $P_{\text{Voigt}}$

Se även

• Atomlinjefilter
• Bomull–Mouton-effekt
• Faraday effekt

Vidare läsning

• Zhao, Zhong-Quan. Exciterade atomlinjefilter . Hämtad 26 mars 2006.