Vattenretentionskurva

Ej att förväxla med psykrometri , egenskaperna hos våt luft.

Vattenretentionskurva för en sand (Ss), antingen silt eller lermylla (Uu), antingen lermylla eller lera (Lu), och antingen lera eller torv (Tt).

Vattenretentionskurvan är förhållandet mellan vattenhalten θ och markvattenpotentialen ψ . Denna kurva är karakteristisk för olika typer av jord, och kallas även för markfuktighetskaraktäristiken .

Det används för att förutsäga markens vattenlagring, vattentillförseln till växterna ( fältkapacitet ) och markaggregatets stabilitet . På grund av den hysteretiska effekten av att vatten fyller och dränerar porerna kan olika vätnings- och torkkurvor urskiljas.

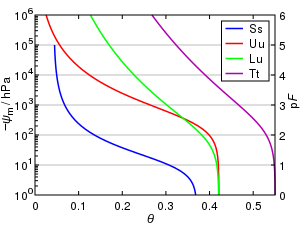
De allmänna särdragen för en vattenretentionskurva kan ses i figuren, där volymen vattenhalt, θ, är plottad mot matrisk potential, $\displaystyle \Psi _{m}}$ . Vid potentialer nära noll är en jord nära mättnad, och vatten hålls i marken främst av kapillärkrafter. När θ minskar blir bindningen av vattnet starkare, och vid små potentialer (mer negativ, närmar sig vissningspunkten ) binds vatten starkt i de minsta porerna, vid kontaktpunkter mellan korn och som filmer bundna av adsorptionskrafter runt partiklar.

Sandiga jordar kommer att involvera huvudsakligen kapillärbindning, och kommer därför att släppa ut det mesta av vattnet vid högre potentialer, medan leriga jordar, med adhesiv och osmotisk bindning, kommer att släppa vatten vid lägre (mer negativa) potentialer. Vid varje given potential kommer torvjordar vanligtvis att uppvisa mycket högre fukthalter än leriga jordar, som skulle förväntas hålla mer vatten än sandjordar. Vattenhållningsförmågan hos vilken jord som helst beror på porositeten och typen av bindning i jorden.

Kurvmodeller

Formen på vattenretentionskurvor kan karakteriseras av flera modeller, en av dem känd som van Genuchten-modellen:

$\theta (\psi )=\theta _{r}+{\frac { \theta _{s}-\theta _{r}}{\left[1+(\alpha |\psi |)^{n}\right]^{1-1/n}}}$

var

$\theta (\psi )$ är vattenretentionskurvan [L ³ L ⁻³ ];

$|\psi |$ är sugtryck ([L] eller cm vatten);

$\theta _{s}$ mättad vattenhalt [L ³ L ⁻³ ];

$\theta _{r}$ kvarvarande vattenhalt [L ³ L ⁻³ ];

$\alpha$ är relaterad till inversen av luftinloppssuget, $\alpha >0$ ([L ⁻¹ ], eller cm ⁻¹ ); och

$n$ är ett mått på porstorleksfördelningen, $n>1$ (dimensionslös).

Baserat på denna parametrisering utvecklades en prediktionsmodell för formen av det omättade hydrauliska konduktivitet-mättnad-tryck-förhållandet.

Historia

1907 skapade Edgar Buckingham den första vattenretentionskurvan. Den mättes och gjordes för sex jordar som varierade i struktur från sand till lera. Uppgifterna kom från experiment gjorda på jordpelare 48 tum höga, där en konstant vattennivå bibehölls cirka 2 tum över botten genom periodisk tillsats av vatten från ett sidorör. De övre ändarna stängdes för att förhindra avdunstning.

Metod

Van Genuchtens parametrar ( $\alpha$ och $n$ ) kan bestämmas genom fält- eller laboratorietestning. En av metoderna är den momentana profilmetoden, där vattenhalten $\theta$ (eller effektiv mättnad $Se$ ) bestäms för en serie sugtrycksmätningar $\psi$ . På grund av ekvationens icke-linjäritet kan numeriska tekniker såsom den icke-linjära minsta kvadratmetoden användas för att lösa van Genuchtens parametrar. Noggrannheten hos de uppskattade parametrarna kommer att bero på kvaliteten på den förvärvade datamängden ( $\theta$ och ${\displaystyle \psi } )$ . När vattenretentionskurvor är försedda med icke-linjära minsta kvadrater kan strukturell över- eller underskattning inträffa. I dessa fall kan representationen av vattenretentionskurvor förbättras i termer av noggrannhet och osäkerhet genom att tillämpa Gaussisk processregression på de residualer som erhålls efter icke-linjära minsta kvadrater. Detta beror mest på korrelationen mellan datapunkterna, som redovisas med Gaussisk processregression genom kärnfunktionen.

Se även

• Jordvatten (retention)

•   Brady, NC (1999). The Nature and Properties of Soils (12:e upplagan). Upper Saddle River, NJ: Prentice-Hall. s. 183–9. ISBN 0-13-852444-0 .

externa länkar

• UNSODA modelldatabas över omättade jordhydrauliska egenskaper ( UNSODA viewer )
• SWRC Anpassa jordhydrauliska modeller till jordvattenretentionsdata