Mekanisk fördel anordning
En enkel maskin som uppvisar mekaniska fördelar kallas en mekanisk fördelsanordning - t.ex.
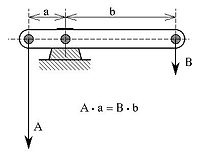
- Spak : Den visade strålen är i statisk jämvikt runt stödpunkten . Detta beror på att momentet som skapas av vektorkraften "A" moturs (moment A *a) är i jämvikt med momentet som skapas av vektorkraften "B" medurs (moment B *b). Den relativt låga vektorkraften "B" översätts till en relativt hög vektorkraft "A" . Kraften ökar alltså i förhållandet mellan krafterna A:B , vilket är lika med förhållandet mellan avstånden till stödpunkten b:a . Detta förhållande kallas den mekaniska fördelen. Denna idealiserade situation tar inte hänsyn till friktion.
- Hjul- och axelrörelser (t.ex. skruvmejslar , dörrhandtag ): Ett hjul är i huvudsak en spak med en arm avståndet mellan axeln och hjulets yttre punkt, och den andra axelns radie. Vanligtvis är detta en ganska stor skillnad, vilket leder till en proportionellt stor mekanisk fördel. Detta gör att även enkla hjul med träaxlar som löper i träblock fortfarande kan svänga fritt, eftersom deras friktion överväldigas av hjulets rotationskraft multiplicerad med den mekaniska fördelen.
- Ett block och tackel med flera remskivor skapar mekaniska fördelar, genom att ha det flexibla materialet ögla över flera remskivor i tur och ordning. Att lägga till fler öglor och remskivor ökar den mekaniska fördelen.
- Skruv : En skruv är i huvudsak ett lutande plan lindat runt en cylinder. Körningen över stigningen av detta lutande plan är den mekaniska fördelen med en skruv.
Remskivor
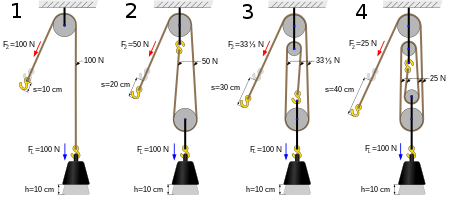
Överväg att lyfta en vikt med rep och remskivor. Ett rep som slingras genom en remskiva som är fäst vid en fast plats, t.ex. en ladugårdstaksparre, och fästs vid vikten kallas en enda remskiva . Den har en mekanisk fördel (MA) = 1 (förutsatt friktionsfria lager i remskivan), och rör sig inte om någon mekanisk fördel (eller nackdel) hur fördelaktig riktningsändringen än kan vara.
En enda rörlig remskiva har MA på 2 (förutsatt friktionsfria lager i remskivan). Tänk på en remskiva som är fäst vid en vikt som lyfts. Ett rep passerar runt den, med ena änden fäst vid en fast punkt ovanför, t.ex. en ladugårdstaksparre, och en dragkraft appliceras uppåt till den andra änden med de två längderna parallella. I denna situation blir avståndet som lyftaren måste dra i repet dubbelt så långt som vikten färdas, vilket gör att kraften som appliceras kan halveras. Notera: om en extra remskiva används för att ändra riktningen på repet, t.ex. personen som utför arbetet vill stå på marken istället för på en takbjälk, ökar inte den mekaniska fördelen.
Genom att slinga fler rep runt fler remskivor kan vi konstruera ett block och tackla för att fortsätta att öka den mekaniska fördelen. Till exempel, om vi har två remskivor fästa på takbjälken, två remskivor fästa på vikten, ena änden fäst vid takbjälken och någon som står på takbjälken och drar i repet, har vi en mekanisk fördel med fyra. Återigen notera: om vi lägger till ytterligare en remskiva så att någon kan stå på marken och dra ner, har vi fortfarande en mekanisk fördel med fyra.
Här är exempel där den fasta punkten inte är uppenbar:
- Ett kardborreband på en sko passerar genom en slits och viks över sig själv. Spåret är en rörlig remskiva och MA = 2.
- Två rep lade ner en ramp fäst vid en upphöjd plattform. En tunna rullas på repen och repen förs över pipan och lämnas till två arbetare längst upp på rampen. Arbetarna drar ihop repen för att få upp pipan till toppen. Pipan är en rörlig remskiva och MA = 2. Om det finns tillräckligt med friktion där repet kläms mellan pipan och rampen blir nyppunkten fästpunkten. Detta anses vara en fast fästpunkt eftersom repet ovanför pipan inte rör sig i förhållande till rampen. Alternativt kan repets ändar fästas på plattformen.
Skruvar
Den teoretiska mekaniska fördelen för en skruv kan beräknas med hjälp av följande ekvation:
var
- d m = skruvgängans medeldiameter
- l = skruvgängans ledning
Observera att den faktiska mekaniska fördelen med ett skruvsystem är större, eftersom en skruvmejsel eller annat skruvdragningssystem också har en mekanisk fördel.
- Lutande plan : MA = lutningens längd ÷ höjden på lutningen
Se även
Anteckningar
Bibliografi
- Fisher, Len (2003), How to Dunk a Doughnut: The Science of Everyday Life , Arcade Publishing, ISBN 978-1-55970-680-3 .
- United States Bureau of Naval Personnel (1971), Grundläggande maskiner och hur de fungerar (Reviderad 1994 utg.), Courier Dover Publications, ISBN 978-0-486-21709-3 .