Vänsterrekursion

I den formella språkteorin för datavetenskap är vänsterrekursion ett specialfall av rekursion där en sträng känns igen som en del av ett språk genom att den bryts ner till en sträng från samma språk (till vänster) och ett suffix (på den rätta). Till exempel $1+2+3$ kännas igen som en summa eftersom den kan delas upp i ${\displaystyle 1+2} ,$ också en summa, och ${}+3$ , ett lämpligt suffix.

När det gäller kontextfri grammatik är en icke-terminal vänsterrekursiv om symbolen längst till vänster i en av dess produktioner är sig själv (vid direkt vänsterrekursion) eller kan göras själv genom någon sekvens av substitutioner (vid indirekt vänster rekursion).

Definition

En grammatik är vänsterrekursiv om och endast om det finns en icke-terminal symbol $A$ som kan härledas till en meningsform med sig själv som symbolen längst till vänster. Symboliskt,

$A\Rightarrow ^{+}A\alpha$ ,

där $\Rightarrow ^{+}$ indikerar operationen att göra en eller flera substitutioner, och $\alpha$ är valfri sekvens av terminala och icketerminala symboler.

Direkt vänsterrekursion

Direkt vänsterrekursion uppstår när definitionen kan tillfredsställas med endast en substitution. Det kräver en formregel

$A\to A\alpha$

där $\alpha$ är en sekvens av icke-terminaler och terminaler . Till exempel regeln

$\displaystyle {\mathit {Expression}}\to {\mathit {Expression}}+{\mathit { Termin}}}$

är direkt vänsterrekursiv. En vänster-till-höger rekursiv descent parser för denna regel kan se ut

  
  
  
  
 void  Uttryck  ()  {  Uttryck  ();  match  (  '+'  );  Term  ();  } 

och sådan kod skulle falla i oändlig rekursion när den körs.

Indirekt vänsterrekursion

Indirekt vänsterrekursion uppstår när definitionen av vänsterrekursion uppfylls via flera substitutioner. Det innebär en uppsättning regler som följer mönstret

$A_{0}\to \beta _{0}A_{1}\alpha _{0}$

$A_{1}\to \beta _{1}A_{2}\alpha _{1}$

$\cdots$

$A_{n}\to \beta _{n}A_{0 }\alpha _{n}$

där $\beta _{0},\beta _{1},\ldots ,\beta _{n}$ är sekvenser som var och en kan ge den tomma strängen , medan $\alpha _{0},\alpha _{1},\ldots ,\alpha _{n}$ kan vara alla sekvenser av terminala och icke-terminala symboler. Observera att dessa sekvenser kan vara tomma. Härledningen

$A_{0}\Rightarrow \beta _{0}A_{1} \alpha _{0}\Rightarrow ^{+}A_{1}\alpha _{0}\Rightarrow \beta _{1}A_{2}\alpha _{1}\alpha _{0}\Rightarrow ^{ +}\cdots \Rightarrow ^{+}A_{0}\alpha _{n}\dots \alpha _{1}\alpha _{0}$

ger sedan $A_{0}$ längst till vänster i sin slutliga meningsform.

Ta bort vänsterrekursion

Vänsterrekursion ställer ofta till problem för analyserare, antingen för att det leder dem till oändlig rekursion (som i fallet med de flesta uppifrån-och-ned-parsare ) eller för att de förväntar sig regler i en normal form som förbjuder det (som i fallet med många nedifrån och upp) parsers , inklusive CYK-algoritmen ). Därför är en grammatik ofta förbearbetad för att eliminera vänsterrekursionen.

Ta bort direkt vänsterrekursion

Den allmänna algoritmen för att ta bort direkt vänsterrekursion följer. Flera förbättringar av denna metod har gjorts. För en vänsterrekursiv icketerminal $A$ , kassera alla regler av formen $A\rightarrow A$ och överväg de som finns kvar:

$A\rightarrow A\alpha _{1}\mid \ldots \mid A\alpha _{n}\mid \beta _ {1}\mid \ldots \mid \beta _{m}$

var:

• varje $\alpha$ är en icke-tom sekvens av icke-terminaler och terminaler, och
• varje $\beta$ är en sekvens av icke-terminaler och terminaler som inte börjar med $A$ .

Ersätt dessa med två uppsättningar produktioner, en uppsättning för $A$ :

$A\rightarrow \beta _{1}A^{\prime }\mid \ldots \mid \beta _{m}A^{\prime }$

och en annan uppsättning för den färska icketerminalen $A'$ (ofta kallad "svansen" eller "resten"):

$A^{\prime }\rightarrow \alpha _{1}A^{\prime }\mid \ldots \mid \alpha _{n }A^{\prime }\mid \epsilon$

Upprepa denna process tills ingen direkt vänsterrekursion återstår.

Som ett exempel, betrakta regeluppsättningen

${\mathit {Expression}}\rightarrow {\mathit {Expression}}+{\mathit {Expression}}\mid {\mathit {Heltal}}\mid {\mathit {String}}$

Detta skulle kunna skrivas om för att undvika vänsterrekursion som

${\mathit {Expression}}\högerpil {\mathit {Heltal}}\,{\mathit {Expression}}'\mid {\mathit {String}}\,{\mathit {Expression}}'$

${\mathit {Expression}}'\rightarrow {}+{\ mathit {Expression}}\,{\mathit {Expression}}'\mid \epsilon$

Tar bort all vänsterrekursion

Genom att etablera en topologisk ordning på icke-terminaler kan ovanstående process utökas till att även eliminera indirekt vänsterrekursion [ :

Inmatningar A grammatik: en uppsättning icke-terminaler $A_{1},\ldots ,A_{n}$ och deras produktioner

Utdata En modifierad grammatik som genererar samma språk men utan vänsterrekursion

1. För varje icke-terminal $A_{i}$ :
   1. Upprepa tills en iteration lämnar grammatiken oförändrad:
      1. För varje regel ${\displaystyle A_{i}\rightarrow \alpha _{i}} är$$\alpha _{i}}$ displaystyle en sekvens av terminaler och icke-terminaler:
         1. Om $\alpha _{i}$ börjar med en icketerminal $A_{j}$ och $j<i$ :
            1. Låt $\beta _{i}$ vara $\alpha _{i}$ utan dess inledande $A_{j}$ .
            2. Ta bort regeln $A_{i}\rightarrow \alpha _{i}$ .
            3. För varje regel $A_{j}\rightarrow \alpha _{j}$ :
               1. Lägg till regeln $A_{i}\rightarrow \alpha _{j} \beta _{i}$ .
   2. Ta bort direkt vänsterrekursion för $A_{i}$ enligt beskrivningen ovan.

Observera att denna algoritm är mycket känslig för den icke-terminala ordningen; optimeringar fokuserar ofta på att välja denna beställning väl.

Fallgropar

Även om ovanstående omvandlingar bevarar språket som genereras av en grammatik, kan de ändra parseträden som bevittnar strängars igenkänning. Med lämplig bokföring trädomskrivning återställa originalen, men om detta steg utelämnas kan skillnaderna ändra semantiken för en analys.

Associativitet är särskilt sårbart; vänsterassociativa operatorer förekommer vanligtvis i högerassociativa-liknande arrangemang under den nya grammatiken. Till exempel, börja med denna grammatik:

$\displaystyle {\mathit {Expression}}\rightarrow {\mathit {Expression}} \,-\,{\mathit {Term}}\mid {\mathit {Term}}}$

${\ mathit {Term}}\rightarrow {\mathit {Term}}\,*\,{\mathit {Factor}}\mid {\mathit {Factor}}$

${\mathit {Factor}}\rightarrow ({\mathit {Expression}})\mid {\mathit {Integer}}$

standardtransformationerna för att ta bort vänsterrekursion ger följande:

$\displaystyle {\mathit {Expression}}\rightarrow {\mathit {Term}}\ {\mathit { Uttryck}}'}$

${\mathit {Expression}}'\rightarrow {} -{\mathit {Term}}\ {\mathit {Expression}}'\mid \epsilon$

${\mathit {Term}}\rightarrow {\mathit {Factor}}\ {\mathit {Term}}'$

${\mathit {Term}}'\rightarrow {}*{\mathit {Factor}}\ {\mathit {Term}}'\mid \epsilon$

${\mathit {Factor}}\högerpil ({\mathit {Uttryck}})\mid {\mathit {Heltal}}$

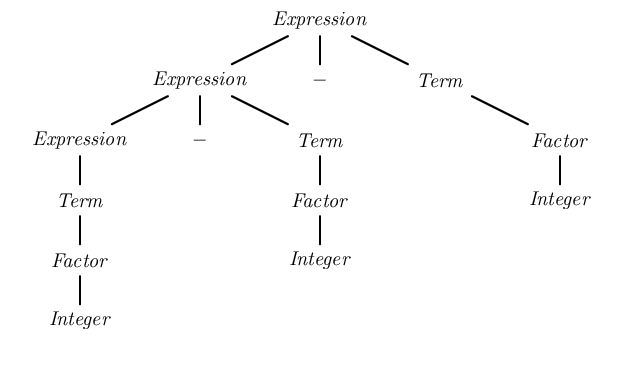
Att analysera strängen "1 - 2 - 3" med den första grammatiken i en LALR-parser (som kan hantera vänsterrekursiva grammatiker) skulle ha resulterat i analysträdet:

Detta analysträd grupperar termerna till vänster, vilket ger korrekt semantik (1 - 2) - 3 .

Att analysera med den andra grammatiken ger

vilket, korrekt tolkat, betyder 1 + (-2 + (-3)), också korrekt, men mindre trogen inmatningen och mycket svårare att implementera för vissa operatörer. Lägg märke till hur termer till höger visas djupare i trädet, ungefär som en högerrekursiv grammatik skulle ordna dem för 1 - (2 - 3) .

Tillmötesgående vänsterrekursion i top-down parsing

En formell grammatik som innehåller vänsterrekursion kan inte tolkas av en LL(k)-parser eller annan naiv rekursiv härkomsttolkare om den inte konverteras till en svagt ekvivalent högerrekursiv form. Däremot är vänsterrekursion att föredra för LALR-parsers eftersom det resulterar i lägre stackanvändning än högerrekursion . Men mer sofistikerade top-down-tolkare kan implementera generella sammanhangsfria grammatiker genom att använda inskränkning. 2006 beskrev Frost och Hafiz en algoritm som rymmer tvetydiga grammatiker med direkt vänsterrekursiva produktionsregler . Den algoritmen utökades till en komplett parsningsalgoritm för att tillgodose indirekt såväl som direkt vänsterrekursion i polynomtid och för att generera kompakta representationer i polynomstorlek av det potentiellt exponentiella antalet parseträd för mycket tvetydiga grammatiker av Frost, Hafiz och Callaghan 2007 Författarna implementerade sedan algoritmen som en uppsättning parserkombinatorer skrivna i programmeringsspråket Haskell .

Se även

• Svansrekursion

externa länkar

• Praktiska överväganden för LALR(1) grammatik