Utdragbar hashing

Extendible hashing är en typ av hashsystem som behandlar en hash som en bitsträng och använder en trie för bucket lookup. På grund av systemets hierarkiska karaktär är omhasning en inkrementell operation (som görs en hink i taget efter behov). Detta innebär att tidskänsliga applikationer påverkas mindre av tabelltillväxt än av vanliga fullbordsrehash.

Extendible hashing beskrevs av Ronald Fagin 1979. Praktiskt taget alla moderna filsystem använder antingen utdragbar hashing eller B-trees . I synnerhet använder det globala filsystemet , ZFS och filsystemet SpadFS utökningsbar hash.

Exempel

Antag att hashfunktionen $h(k)$ returnerar en sträng med bitar. De första i-bitarna av varje sträng kommer att användas som index för att ta reda på var de kommer att hamna i "katalogen" (hashtabellen). Dessutom är i det minsta talet så att indexet för varje objekt i tabellen är unikt.

Nycklar som ska användas:

{\begin{aligned}h(k_{1})=100100\\h(k_{2})=010110 \\h(k_{3})=110110\end{aligned}}

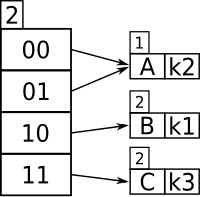
Låt oss anta att för det här specifika exemplet är skopstorleken 1. De två första nycklarna som ska infogas, k ₁ och k ₂ , kan särskiljas med den mest signifikanta biten och infogas i tabellen enligt följande:

Nu, om k ₃ skulle hashas till bordet, skulle det inte räcka att särskilja alla tre nycklar med en bit (eftersom både k ₃ och k ₁ har 1 som sin bit längst till vänster). Dessutom, eftersom skopstorleken är en, skulle bordet svämma över. Eftersom att jämföra de två första mest signifikanta bitarna skulle ge varje nyckel en unik plats, fördubblas katalogstorleken enligt följande:

Och så nu har k ₁ och k ₃ en unik plats, som särskiljs av de två första bitarna längst till vänster. Eftersom k ₂ är i den övre halvan av tabellen, pekar både 00 och 01 på den eftersom det inte finns någon annan nyckel att jämföra med som börjar med en 0.

Ovanstående exempel är från Fagin et al. (1979) .

Ytterligare detaljer

h(k_{4})=011110

Nu måste k ₄ infogas, och den har de två första bitarna som 01..(1110), och med ett 2-bitars djup i katalogen, mappar detta från 01 till hink A. Hink A är full (max storlek 1 ), så det måste delas; eftersom det finns mer än en pekare till Bucket A, finns det inget behov av att öka katalogstorleken.

Det som behövs är information om:

Nyckelstorleken som mappar katalogen (det globala djupet), och
Nyckelstorleken som tidigare har kartlagt hinken (det lokala djupet)

För att skilja de två åtgärdsfallen:

Fördubbling av katalogen när en hink blir full
Skapa en ny hink och omfördelning av posterna mellan den gamla och den nya hinken

När man undersöker det initiala fallet med en utökningsbar hashstruktur, om varje katalogpost pekar på en hink, bör det lokala djupet vara lika med det globala djupet.

Antalet katalogposter är lika med 2 ^{globala djup} , och det initiala antalet hinkar är lika med 2 ^{lokala djup} .

⁰ Således om globalt djup = lokalt djup = 0, då 2 = 1, så en initial katalog med en pekare till en hink.

Tillbaka till de två åtgärdsfallen; om hinken är full:

Om det lokala djupet är lika med det globala djupet, så finns det bara en pekare till hinken, och det finns inga andra katalogpekare som kan mappas till hinken, så katalogen måste fördubblas.
Om det lokala djupet är mindre än det globala djupet finns det mer än en pekare från katalogen till hinken, och hinken kan delas.

Nyckel 01 pekar på Bucket A, och Bucket A:s lokala djup på 1 är mindre än katalogens globala djup på 2, vilket betyder att nycklar som hashas till Bucket A endast har använt ett 1-bitars prefix (dvs. 0), och hinken måste ha sitt innehåll delas med tangenterna 1 + 1 = 2 bitar i längd; i allmänhet, för varje lokalt djup d där d är mindre än D, det globala djupet, då måste d ökas efter en hinkdelning, och det nya d används som antalet bitar av varje posts nyckel för att omfördela ingångarna i den tidigare hink i de nya hinkarna.

Nu,

h(k_{4})=011110

provas igen, med 2 bitar 01.., och nu pekar nyckel 01 på en ny hink men det finns fortfarande $k_{2}$ i den ( $h(k_) {2})=010110$ och börjar även med 01).

Om $k_{2}$ hade varit 000110, med nyckel 00, skulle det inte ha varit några problem, eftersom $k_{2}$ skulle ha blivit kvar i den nya hinken A' och hinken D skulle har varit tomma.

(Detta skulle ha varit det absolut mest sannolika fallet när hinkar är större än 1 och de nyligen delade hinkarna skulle vara ytterst osannolikt att svämma över, såvida inte alla poster var omhaskade till en hink igen. Men bara för att betona rollen av djupinformationen kommer exemplet att följas logiskt till slutet.)

Så hink D måste delas upp, men en kontroll av dess lokala djup, som är 2, är samma som det globala djupet, som är 2, så katalogen måste delas upp igen för att hålla nycklar med tillräcklig detalj, t.ex. 3 bitar.

Hink D måste delas på grund av att den är full.
Eftersom D:s lokala djup = det globala djupet, måste katalogen fördubblas för att öka bitdetaljerna i nycklar.
Det globala djupet har ökat efter att katalogen delats upp till 3.
Den nya posten $k_{4}$ nyckels om med globalt djup 3 bitar och hamnar i D som har lokalt djup 2, som nu kan ökas till 3 och D kan delas upp till D' och E.
Innehållet i den delade hinken D, $k_{2}$ , har nycklarats med 3 bitar, och det hamnar i D'.
K4 provas igen och den hamnar i E som har en reservplats.

Nu är $h(k_{2})=010110$ i D och $h(k_{4})=011110$ provas igen, med 3 bitar 011.., och den pekar på hink D som redan innehåller $k_{2}$ så är full; D:s lokala djup är 2 men nu är det globala djupet 3 efter katalogfördubblingen, så nu kan D delas upp i hinkens D' och E, innehållet i D, k 2 {\displaystyle k_ $har$ sitt $h(k_{2})$ försökte igen med en ny global djupbitmask på 3 och $k_{2}$ hamnar i D', sedan den nya posten $k_{ 4}$ försöks igen med $h(k_{4})$ bitmaskerad med det nya globala djupbiträkningen på 3 och detta ger 011 som nu pekar på en ny hink E som är tom. Så $k_{4}$ går i hink E.

Exempel implementering

Nedan är den utvidgbara hashalgoritmen i Python , med kopplingen till skivblocket/minnessidan, caching och konsistensproblem borttagna. Observera att det finns ett problem om djupet överstiger bitstorleken för ett heltal, eftersom dubblering av katalogen eller uppdelning av en hink gör det inte möjligt för poster att omhashas till olika hinkar.

Koden använder de minst signifikanta bitarna , vilket gör det mer effektivt att expandera tabellen, eftersom hela katalogen kan kopieras som ett block ( Ramakrishnan & Gehrke (2003) ).

Python exempel

  

 
       
          
          0

       
           

         
             
               
                 
                
         

      
            
               
                 

     
         

 
       
          0
          

      
          
               

         
          
          
         
         
               
                  
                  

              
              
                  
              
                
                  
                        
                 

                     
                        

      
         

   
      
      
      

     
    
       
         
    

       
         PAGE_SZ  =  10  klass  Sida  :  def  __init__  (  själv  )  ->  Ingen  :  själv  .  karta  =  []  själv  .  local_depth  =  def  full  (  self  )  ->  bool  :  return  len  (  self  .  map  )  >=  PAGE_SZ  def  put  (  self  ,  k  ,  v  )  ->  None  :  for  i  ,  (  nyckel  ,  värde  )  i  enumerate  (  self  .  map  ):  om  nyckel  ==  k  :  del  själv  .  karta  [  i  ]  bryta  själv  .  karta  .  append  ((  k  ,  v  ))  def  get  (  jag  ,  k  ):  för  nyckel  ,  värde  i  själv  .  map  :  if  key  ==  k  :  returvärde  def  get_local_high_bit  (  self  )  :  return  1  <<  self  .  local_depth  class  ExtendibleHashing  :  def  __init__  (  self  )  ->  None  :  self  .  global_depth  =  själv  .  katalog  =  [  Sida  ()]  def  get_page  (  själv  ,  k  ):  h  =  hash  (  k  )  returnera  själv  .  katalog  [  h  &  ((  1  <<  self  .  global_depth  )  -1  )  ]  def  put  (  self  ,  k  ,  v  )  ->  None  :  p  =  self  .  get_page  (  k  )  full  =  p  .  full  ()  sid  .  sätta  (  k  ,  v  )  om  full  :  om  p  .  local_depth  ==  själv  .  global_depth  :  själv  .  katalog  *=  2  själv  .  global_depth  +=  1  p0  =  Sida  ()  p1  =  Sida  ()  p0  .  local_depth  =  p1  .  local_depth  =  p  .  local_depth  +  1  high_bit  =  p  .  get_local_high_bit  ()  för  k2  ,  v2  i  p  .  map  :  h  =  hash  (  k2  )  new_p  =  p1  om  h  &  high_bit  annat  p0  new_p  .  sätta  (  k2  ,  v2  )  för  i  i  intervallet  (  hash  (  k  )  &  (  hög_bit  -  1  ),  len  (  själv  .  katalog  ),  hög_bit  ):  själv  .  katalog  [  i  ]  =  p1  om  i  &  high_bit  annat  p0  def  get  (  self  ,  k  ):  returnera  själv  .  get_page  (  k  )  .  få  (  k  )  om  __name__  ==  "__main__"  :  eh  =  ExtendibleHashing  ()  N  =  10088  l  =  lista  (  intervall  (  N  ))  importera  slumpmässigt  slumpmässigt  .  blanda  (  l  )  för  x  i  l  :  eh  .  sätta  (  x  ,  x  )  print  (  l  )  för  i  inom  intervallet  (  N  ):  print  (  eh  .  få  (  i  ))

Anteckningar

Se även

Fagin, R.; Nievergelt, J.; Pippenger, N.; Strong, HR (september 1979), "Extendible Hashing - A Fast Access Method for Dynamic Files", ACM Transactions on Database Systems , 4 (3): 315–344, doi : 10.1145/320083.320092 , S2CID 2723599
Ramakrishnan, R.; Gehrke, J. (2003), Database Management Systems, 3:e upplagan: Kapitel 11, Hash-Based Indexing , s. 373–378
Silberschatz, Abraham ; Korth, Henry ; Sudarshan, S., Database System Concepts, sjätte upplagan: Kapitel 11.7, Dynamic Hashing

externa länkar

Den här artikeln innehåller material som är allmän egendom från Paul E. Black. "Utvidgbar hashning" . Ordbok över algoritmer och datastrukturer . NIST .
Extendible Hashing-anteckningar vid Arkansas State University
Utdragbara hashing-anteckningar
Bilder från databasen System Concepts bok om utvidgbar hashning för hashbaserade dynamiska index