Unikt färgbar graf
I grafteorin är en unikt färgbar graf en k- kromatisk graf som bara har en möjlig (riktig) k - färgning upp till permutation av färgerna. På motsvarande sätt finns det bara ett sätt att dela upp dess hörn i k oberoende mängder och det finns inget sätt att dela upp dem i k − 1 oberoende mängder.
Exempel
En komplett graf är unikt färgbar, eftersom den enda korrekta färgen är en som tilldelar varje vertex en annan färg.
Varje k -träd är unikt ( k + 1)-färgbart. De unikt 4-färgbara plana graferna är kända för att vara exakt de apolloniska nätverken , det vill säga de plana 3-träden.
Varje ansluten tvådelad graf är unikt 2-färgbar. Dess 2-färgning kan erhållas genom att välja en startpunkt godtyckligt, färga topparna på jämnt avstånd från startpunkten med en färg och färga topparna på udda avstånd från startpunkten med den andra färgen.
Egenskaper
Några egenskaper hos en unikt k -färgbar graf G med n hörn och m kanter:
- m ≥ ( k - 1) n - k ( k -1)/2.
Relaterade begrepp
Minimal ofullkomlighet
En minimal imperfekt graf är en graf där varje subgraf är perfekt . Borttagningen av valfri hörn från en minimal imperfekt graf lämnar en unik färgbar subgraf.
Unik kantfärgbarhet
En unikt kantfärgad graf är en k -kant-kromatisk graf som bara har en möjlig (riktig) k -kantfärgning upp till permutation av färgerna. De enda unika 2-kantsfärgbara graferna är banorna och cyklerna. För varje k är stjärnorna K 1, unikt k k - kantfärgbara. Dessutom Wilson (1976) och Thomason (1978) bevisade att när k ≥ 4 är de också de enda medlemmarna i denna familj. Det finns dock unika 3-kants-färgbara grafer som inte passar in i denna klassificering, till exempel grafen för den triangulära pyramiden .
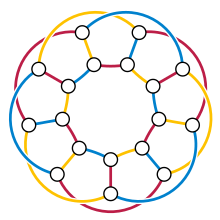
Om en kubisk graf är unikt 3-kantsfärgbar, måste den ha exakt tre Hamiltonska cykler , bildade av kanterna med två av dess tre färger, men vissa kubiska grafer med endast tre Hamiltonska cykler är inte unikt 3-kantsfärgbara. Varje enkel plan kubisk graf som är unikt 3-kantsfärgbar innehåller en triangel, men WT Tutte ( 1976 ) observerade att den generaliserade Petersen-grafen G (9,2) är icke-plan , triangelfri och unikt 3-kantig- färgbar. Under många år var det den enda kända grafen, och den hade antagits vara den enda sådana grafen, men nu är oändligt många triangelfria, icke-plana kubiska, unika 3-kantsfärgbara grafer kända.
Unik total färgbarhet
En unik total färgbar graf är en k -total-kromatisk graf som bara har en möjlig (riktig) k -total-färgning upp till permutation av färgerna.
Tomma grafer , banor och längdcykler som är delbara med 3 är unikt totalt färgbara grafer. Mahmoodian & Shokrollahi (1995) förmodade att de också är de enda medlemmarna i denna familj.
Några egenskaper hos en unikt k -total-färgbar graf G med n hörn:
- χ″( G ) = Δ( G ) + 1 om inte G = K2 .
- A( G ) ≤ 2 5( G ).
- Δ( G ) ≤ n/2 + 1.
Här är χ″( G ) det totala kromatiska talet ; Δ( G ) är den maximala graden ; och δ( G ) är den lägsta graden .
Anteckningar
- Akbari, S. (2003), "Two conjectures on uniquely totally colorable graphs", Discrete Mathematics , 266 (1–3): 41–45, doi : 10.1016/S0012-365X(02)00797-5 , MR 59 .
- Akbari, S.; Behzad, M.; Hajiabolhassan, H.; Mahmoodian, ES (1997), "Uniquely total colorable graphs", Graphs and Combinatorics , 13 (4): 305–314, doi : 10.1016/S0012-365X(02)00797-5 , MR 1485924 .
- belcastro, sarah-marie ; Haas, Ruth (2015), "Triangel-free uniquely 3-edge colorable cubic graphs", Contributions to Discrete Mathematics , 10 (2): 39–44, arXiv : 1508.06934 , doi : 10.11575/cdm.9015/cdm.9015/cdm.9015/cdm.9015 / cdm.9015 / cdm.9010 .
- Bollobás, Béla (1978), Extremal Graph Theory , LMS Monographs, vol. 11, Academic Press, MR 0506522 .
- Fowler, Thomas (1998), Unique Coloring of Planar Graphs (PDF) , Ph.D. avhandling, Georgia Institute of Technology Mathematics Department .
- Hillar, Christopher J.; Windfeldt, Troels (2008), "Algebraic characterization of uniquely vertex colorable graphs", Journal of Combinatorial Theory , Series B, 98 (2): 400–414, arXiv : math/0606565 , doi : 10.1016/j.007ctb.82. 004 , MR 2389606 .
- Mahmoodian, ES (1998), "Defining sets and uniqueness in graph colorings: a survey", Journal of Statistical Planning and Inference , 73 (1–2): 85–89, doi : 10.1016/S0378-3758(98)00053- 6 , MR 1655213 .
- Mahmoodian, ES; Shokrollahi, MA (1995), "Öppna problem vid kombinatorikverkstaden i AIMC25 (Tehran, 1994)", i CJ, Colbourn ; ES, Mahmoodian (red.), Combinatorics Advances , Mathematics and its applications, vol. 329, Dordrecht; Boston; London: Kluwer Academic Publishers, s. 321–324 .
- Schwenk, Allen J. (1989), "Enumeration of Hamiltonian cycles in certain generalized Petersen graphs", Journal of Combinatorial Theory , Series B, 47 (1): 53–59, doi : 10.1016/0095-8956(89)90064- 6 , MR 1007713 .
- Thomason, AG (1978), "Hamiltonian cycles and uniquely edge colourable graphs", Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977) , Annals of Discrete Mathematics, vol. 3, sid. 259-268, MR 0499124 .
- Thomason, Andrew (1982), "Cubic graphs with three Hamiltonian cycles are not always uniquely edge colorable", Journal of Graph Theory , 6 (2): 219–221, doi : 10.1002/jgt.3190060218 , MR 0655209 .
- Truszczyński, M. (1984), "Några resultat på unikt färgbara grafer", i Hajnal, A. ; Lovász, L .; Sós, VT (red.), Finita och oändliga uppsättningar. Vol. I, II. Förhandlingar om det sjätte ungerska kombinatoriska kollokviet som hölls i Eger, 6–11 juli 1981, Colloq. Matematik. Soc. János Bolyai, vol. 37, North-Holland, Amsterdam, s. 733–748, MR 0818274 .
- Tutte, William T. (1976), "Hamiltonian circuits", Colloquio Internazionale sulle Teorie Combinatorie (Rom, 1973), Tomo I , Accad. Naz. Lincei, Rom, s. 193–199. Atti dei Convegni Lincei, nr 17, MR 0480185 . Som citeras av belcastro & Haas (2015) .
- Xu, Shao Ji (1990), "The size of uniquely colorable graphs", Journal of Combinatorial Theory , Series B, 50 (2): 319–320, doi : 10.1016/0095-8956(90)90086-F , MR 508123 .
- Wilson, RJ (1976), "Problem 2", i Nash-Williams, C. St. JA ; Sheehan, J. (red.), Proc. British Comb. Konf. 1975 , Winnipeg: Utilitas Math., sid. 696 . Som citeras av Thomason (1978) .