Tröghetsvåg

Ekvatorial tröghetsvågspuls orsakade mönster av vätskeflöde inuti en stadigt roterande sfärisk kammare. Pilar på detta tvärsnitt visar flödets riktning och styrka i ekvatorialplanet när sfären fortsätter att rotera medurs på sin axel som visas till vänster. Rött indikerar flöde ut ur planet; blått indikerar flöde in i planet.

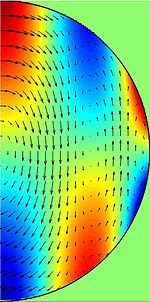
Tröghetsvågor , även kända som tröghetssvängningar , är en typ av mekaniska vågor som är möjliga i roterande vätskor . Till skillnad från yttyngdkraftsvågor som vanligtvis ses på stranden eller i badkaret, flyter tröghetsvågor genom vätskans inre, inte vid ytan. Liksom alla andra typer av vågor orsakas en tröghetsvåg av en återställande kraft och kännetecknas av dess våglängd och frekvens . Eftersom återställningskraften för tröghetsvågor är Corioliskraften, är deras våglängder och frekvenser relaterade på ett märkligt sätt. Tröghetsvågor är tvärgående . Oftast observeras de i atmosfärer, hav, sjöar och laboratorieexperiment. Rossby-vågor , geostrofiska strömmar och geostrofiska vindar är exempel på tröghetsvågor. Tröghetsvågor finns sannolikt också i den smälta kärnan av den roterande jorden .

Återställande kraft

Tröghetsvågor återställs till jämvikt av Corioliskraften , ett resultat av rotation. För att vara exakt uppstår Corioliskraften (tillsammans med centrifugalkraften ) i en roterande ram för att förklara det faktum att en sådan ram alltid accelererar. Tröghetsvågor kan därför inte existera utan rotation. Corioliskraften är mer komplicerad än spänning på en sträng och verkar i en 90° vinkel mot rörelseriktningen, och dess styrka beror på vätskans rotationshastighet. Dessa två egenskaper leder till tröghetsvågornas speciella egenskaper.

Egenskaper

Tröghetsvågor är möjliga endast när en vätska roterar och finns i huvuddelen av vätskan, inte vid dess yta. Liksom ljusvågor är tröghetsvågor tvärgående , vilket innebär att deras vibrationer uppträder vinkelrätt mot vågens färdriktning. En märklig geometrisk egenskap hos tröghetsvågor är att deras fashastighet , som beskriver rörelsen av vågens toppar och dalar , är vinkelrät mot deras grupphastighet , vilket är ett mått på energins utbredning.

Medan en ljudvåg eller en elektromagnetisk våg av vilken frekvens som helst är möjlig, kan tröghetsvågor existera endast över frekvensområdet från noll till två gånger vätskans rotationshastighet. Dessutom bestäms vågens frekvens av dess färdriktning. Vågor som rör sig vinkelrätt mot rotationsaxeln har noll frekvens och kallas ibland för geostrofiska lägen. Vågor som rör sig parallellt med axeln har maximal frekvens (dubbla rotationshastigheten), och vågor i mellanliggande vinklar har mellanfrekvenser. I fritt utrymme kan en tröghetsvåg existera vid vilken frekvens som helst mellan 0 och två gånger rotationshastigheten. En sluten behållare kan emellertid införa begränsningar för de möjliga frekvenserna av tröghetsvågor, som det kan för alla typer av vågor. Tröghetsvågor i en sluten behållare kallas ofta tröghetslägen . I en sfär, till exempel, tvingas tröghetslägena att anta diskreta frekvenser, vilket lämnar luckor där inga lägen kan existera.

Exempel på tröghetsvågor

Alla typer av vätska kan stödja tröghetsvågor: vatten, olja, flytande metaller, luft och andra gaser. Tröghetsvågor observeras vanligast i planetariska atmosfärer ( Rossby-vågor , geostrofiska vindar ) och i hav och sjöar ( geostrofiska strömmar ), där de är ansvariga för mycket av den blandning som sker. Tröghetsvågor som påverkas av havsbottens lutning kallas ofta för Rossbyvågor . Tröghetsvågor kan observeras i laboratorieexperiment eller i industriella flöden där en vätska roterar. Tröghetsvågor finns sannolikt också i den flytande yttre kärnan av jorden, och åtminstone en grupp [ 1] har hävdat bevis på dem. På samma sätt är tröghetsvågor sannolikt i roterande astronomiska flöden som stjärnor , ansamlingsskivor , planetariska ringar och galaxer .

Matematisk beskrivning

Vätskeflödet styrs av Navier-Stokes ekvation för momentum. Flödeshastigheten ${\vec {u}}$ för en vätska med viskositet $\nu$ under tryck ${\displaystyle P} och roterande$ med hastigheten $\Omega$ ändras över tiden $t$ enligt

${\frac {\partial {\vec {u}}}{\partial t}}+({\vec {u}}\cdot {\vec {\nabla }}){\vec {u}} =-{\frac {1}{\rho }}{\vec {\nabla }}P+\nu \nabla ^{2}{\vec {u}}-2{\vec {\Omega }}\times { \vec {u}}.$

Den första termen till höger står för tryck, den andra står för viskös diffusion och den tredje (sista) termen på höger sida av momentumekvationen (ovan) är Coriolis-termen.

För att vara exakt är ${\vec {u}}$ flödeshastigheten som observeras i den roterande referensramen. Eftersom en roterande referensram accelererar (dvs. icke-tröghetsram), uppstår två ytterligare (pseudo) krafter (som nämnts ovan) som ett resultat av denna koordinattransformation: centrifugalkraften och Corioliskraften. I ekvationen ovan ingår centrifugalkraften som en del av det generaliserade trycket ${\displaystyle P} ,$ det vill säga $P$ är relaterat till det vanliga trycket $p$ , beroende på avståndet från rotationsaxeln $r$ , by

$P=p+{\frac {1}{2}}\rho r^{2}\Omega ^{2}.$

I det fall där rotationshastigheten är stor blir Corioliskraften och centrifugalkraften stora jämfört med de andra termerna. Eftersom de är små i jämförelse kan diffusion och den "konvektiva derivatan" (andra termen till vänster) utelämnas. Att ta en krullning av båda sidor och tillämpa några vektoridentiteter är resultatet

${\frac {\partial }{\partial t}}\nabla \times {\vec {u}}=2({\vec {\Omega }}\cdot {\vec {\nabla }}){ \vec {u}}.$

En klass av lösningar till denna ekvation är vågor som uppfyller två villkor. Först, om ${\vec {k}}$ är vågvektorn ,

${\vec {u}}\cdot {\vec {k}}=0,$

det vill säga vågorna måste vara tvärgående, som nämnts ovan. För det andra krävs att lösningar har en frekvens $\omega$ som uppfyller spridningsrelationen

$\omega =2{\hat {k}}\cdot {\vec {\Omega }}=2\Omega \cos {\theta },$

där $\theta$ är vinkeln mellan rotationsaxeln och vågens riktning. Dessa speciella lösningar är kända som tröghetsvågor.

Dispersionsrelationen ser ungefär ut som Coriolis-termen i momentumekvationen - lägg märke till rotationshastigheten och faktorn två. Det innebär omedelbart intervallet för möjliga frekvenser för tröghetsvågor, såväl som beroendet av deras frekvens på deras riktning.

Vidare läsning

•   Aldridge, KD; I. Lumb (1987). "Tröghetsvågor identifierade i jordens flytande yttre kärna". Naturen . 325 (6103): 421–423. Bibcode : 1987Natur.325..421A . doi : 10.1038/325421a0 . S2CID 4312055 .
• Greenspan, HP (1969). Teorin om roterande vätskor . Cambridge University Press.
•   Landau, LD; EM Lifschitz (1987). Fluid Mechanics, andra upplagan . New York: Elsevier. ISBN 978-0-7506-2767-2 .