Szemerédi regelbundenhet lemma

Kanterna mellan delarna beter sig på ett "slumpmässigt" sätt.

Szemerédis regularitetslemma är ett av de mest kraftfulla verktygen inom extremal grafteori , särskilt i studiet av stora täta grafer. Den anger att hörnen på varje tillräckligt stor graf kan delas upp i ett begränsat antal delar så att kanterna mellan olika delar beter sig nästan slumpmässigt.

Enligt lemma kan vi, oavsett hur stor en graf är, approximera den med kanttätheterna mellan ett begränsat antal delar. Mellan två valfria delar kommer fördelningen av kanter att vara pseudoslumpmässig enligt kanttätheten. Dessa approximationer ger i huvudsak korrekta värden för olika egenskaper hos grafen, såsom antalet inbäddade kopior av en given subgraf eller antalet kantborttagningar som krävs för att ta bort alla kopior av någon subgraf.

Påstående

För att formellt ange Szemerédis regelbundenhetslemma måste vi formalisera vad kantfördelningen mellan delar som beter sig 'nästan slumpmässigt' egentligen betyder. Med "nästan slumpmässigt" syftar vi på ett begrepp som kallas ε -regelbundenhet. För att förstå vad detta innebär anger vi först några definitioner. det följande är G en graf med vertexuppsättning V .

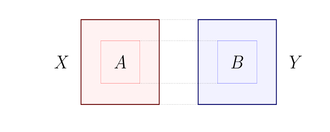
Definition 1. Låt X , Y vara disjunkta delmängder av V . Kantdensiteten för paret ( X : Y ) , definieras som

$d(X,Y):={\frac {\left|E(X,Y)\right|}{|X||Y|}}$

där E ( X , Y ) anger uppsättningen av kanter som har en ändpunkt i X och en i Y.

Delmängdspar av ett vanligt par liknar det ursprungliga paret i kanttäthet.

Vi kallar ett par delar ε -regular om, när du tar en stor delmängd av varje del, deras kanttäthet inte är alltför långt från kanttätheten för paret av delar. Formellt,

Definition 2. För ε > 0 kallas ett par av vertexmängder X och Y ε -regular , om för alla delmängder A ⊆ X , B ⊆ Y uppfyller | A | ≥ ε| X | , | B | ≥ ε| Y | , vi har

$\left|d(X,Y)-d(A,B)\right|\leq \varepsilon .$

Det naturliga sättet att definiera en ε -regular partition bör vara en där varje par av delar är ε -regular. Vissa grafer, som de halva graferna , kräver dock att många par av partitioner (men en liten del av alla par) är oregelbundna. Så vi ska definiera ε -regelbundna partitioner som en där de flesta par av delar är ε -regelbundna.

Definition 3. En partition av $V$ i $k$ sätter ${\mathcal {P}}=\{V_{1},\ ldots ,V_{k}\}$ kallas en $\varepsilon$ -vanlig partition om

$\sum _{(V_{i},V_{j}){\text{ inte }}\varepsilon {\text{-regular}}}|V_{i}||V_{j}|\ leq \varepsilon |V(G)|^{2}$

Nu kan vi säga lemmat:

Szemerédis Regularity Lemma. För varje ε > 0 och positivt heltal m finns det ett heltal M så att om G är en graf med minst M hörn, finns det ett heltal k i området m ≤ k ≤ M och en ε -reguljär partition av vertexmängden av G till k uppsättningar.

Gränsen M för antalet delar i grafens partition som ges av bevisen för Szemeredis regularitetslemma är mycket stor, givet av en O(ε ⁻⁵ ) -nivå itererad exponential av m . En gång hoppades man att den verkliga gränsen var mycket mindre, vilket skulle ha haft flera användbara tillämpningar. Men Gowers (1997) hittade exempel på grafer för vilka M verkligen växer mycket snabbt och är minst lika stor som en ε ^−1/16 -nivå itererad exponential av m . I synnerhet den bästa gränsen har nivå exakt 4 i Grzegorczyk-hierarkin , och är alltså inte en elementär rekursiv funktion .

Bevis

Gränserna för delmängder som bevittnar oegentligheter förfinar varje del av partitionen.

Vi ska hitta en ε-regelbunden partition för en given graf efter en algoritm. En grov översikt:

1. Börja med en godtycklig partition (kan bara vara 1 del)
2. Medan partitionen inte är ε-regelbunden:
   • Hitta de delmängder som uppvisar ε-oregelbundenhet för varje oregelbundet par.
   • Förfina partitionen samtidigt genom att använda alla bevittande delmängder.

Vi använder en teknik som kallas energiökningsargumentet för att visa att denna process avslutas efter ett begränsat antal steg. I grund och botten definierar vi en monovariant som måste öka med en viss mängd i varje steg, men den är avgränsad ovan och kan därför inte öka på obestämd tid. Denna monovariant kallas 'energi' eftersom det är en $L^{2}$ kvantitet.

Definition 4. Låt U , W vara delmängder av V . Ställ in $|V|=n$ . Energin för paret ( U : W ) , definieras som

$q(U,W):={\frac {|U||W|}{n^{2}}}d(U,W)^{2}$

För partitioner ${\mathcal {P}}_{U}=\{U_{1},\ldots ,U_{k}\}$ av U och ${\mathcal {P}}_{W}=\{W_{1},\ldots ,W_{l}\}$ av W definierar vi energin att vara summan av energierna mellan varje par av delar:

${\displaystyle q({\mathcal {P}}_{U},{\mathcal {$

Slutligen, för en partition ${\mathcal {P}}=\{V_{1},\ldots ,V_{k}\}$ av V , definiera energin av ${\mathcal {P}}$ ska vara $q({\mathcal {P}},{\mathcal {P}})$ . Specifikt,

$q({\mathcal {P}})=\sum _{i=1}^{k}\sum _{j=1}^{k}q (V_{i},V_{j})=\summa _{i=1}^{k}\summa _{j=1}^{k}{\frac {|V_{i}||V_{j }|}{n^{2}}}d(V_{i},V_{j})^{2}$

Observera att energin är mellan 0 och 1 eftersom kantdensiteten begränsas ovanför av 1:

$q({\mathcal {P}})=\sum _{i=1}^{k}\summa _{j=1}^{k}{\frac {|V_{i }||V_{j}|}{n^{2}}}d(V_{i},V_{j})^{2}\leq \sum _{i=1}^{k}\summa _ {j=1}^{k}{\frac {|V_{i}||V_{j}|}{n^{2}}}=1$

Nu börjar vi med att bevisa att energin inte minskar vid förfining.

Lemma 1. (Energien minskar inte vid partitionering) För alla partitioner ${\mathcal {P}}_{U}$ och ${\mathcal {P}}_{W}$ i vertex sätter $\displaystyle U}$$q({\mathcal {P}}_{U},{\mathcal {P}}_{W})\geq q(U,W)$ och $W$ , .

Bevis: Låt ${\mathcal {P}}_{U}=\{U_{1},\ldots ,U_{k}\}$ och ${\mathcal {P}}_{W}=\{W_{1},\ldots ,W_{l}\}$ . Välj hörn $x$ enhetligt från $U$ och $y$ enhetligt från $W$ , med $x$ i del $U_{i}$ och $y$ i del $W_{j}$ . Definiera sedan den slumpmässiga variabeln $Z=d(U_{i},W_{j})$ . Låt oss titta på egenskaperna hos $Z$ . Förväntningen är

$\mathbb {E} [Z]=\summa _{i=1}^{k}\summa _{j=1}^{l}{\frac {|U_{ i}|}{|U|}}{\frac {|W_{j}|}{|W|}}d(U_{i},W_{j})={\frac {e(U,W) }{|U||W|}}=d(U,W)$

Det andra ögonblicket är

$summa _{i=1}^{k}\summa _{j=1}^{l}{\ frac {|U_{i}|}{|U|}}{\frac {|W_{j}|}{|W|}}d(U_{i},W_{j})^{2}={ \frac {n^{2}}{|U||W|}}q({\mathcal {P}}_{U},{\mathcal {P}}_{W})}$

Genom konvexitet, $\mathbb {E} [Z^{2}]\geq \mathbb {E} [Z]^{2}$ . Om vi ​​arrangerar om får vi att ${\displaystyle q({\mathcal {P}}_{U},{\mathcal {P}}_{W})$ för alla $U,W$ . $\square$

Om varje del av ${\mathcal {P}}$ partitioneras ytterligare, kallas den nya partitionen en förfining av ${\mathcal {P}}$ . Nu, om ${\displaystyle {\mathcal {P}}=\{V_{1},\ldots ,V_{m}\}} ,$ tillämpa Lemma 1 på varje par $(V_{i},V_{j})$ bevisar att för varje förfining ${\mathcal {P'}}$ av ${\mathcal {P }}$ , $q({\mathcal {P'}})\geq q({\mathcal {P}})$ . Förfiningssteget i algoritmen förlorar alltså ingen energi.

Lemma 2. (Energiförstärkningslemma) Om $(U,W)$ inte är $\varepsilon$ -regular som bevittnas av $U_ {1}\subset U,W_{1}\subset W$ , sedan,

$q\left(\{U_{1},U\backslash U_{1}\},\{W_{1},W\backslash W_{1}\}\right)>q(U, W)+\varepsilon ^{4}{\frac {|U||W|}{n^{2}}}$

Bevis: Definiera $Z$ enligt ovan. Sedan,

$Var(Z)=\mathbb {E} [Z^{2} ]-\mathbb {E} [Z]^{2}={\frac {n^{2}}{|U||W|}}\left(q\left(\{U_{1},U\ snedstreck U_{1}\},\{W_{1},W\backslash W_{1}\}\right)-q(U,W)\right)$

Men observera att $|Z-\mathbb {E} [Z]|=|d(U_{1},W_{1})-d(U,W)|$ med sannolikhet ${\displaystyle {\frac {|U_{1}|}{|U|}}{\frac {|W_{1}|}{|W|}}} (motsvarande x ∈$ U $x\ i U_{1}}$ och $y\in W_{1}$ ), så

$Var(Z)=\mathbb {E} [(Z-\mathbb {E} [Z] )^{2}]\geq {\frac {|U_{1}|}{|U|}}{\frac {|W_{1}|}{|W|}}(d(U_{1}, W_{1})-d(U,W))^{2}>\varepsilon \cdot \varepsilon \cdot \varepsilon ^{2}$$\square$

Nu kan vi bevisa energiökningsargumentet, som visar att energin ökar avsevärt i varje iteration av algoritmen.

Lemma 3 (Energiökningslemma) Om en partition ${\mathcal {P}}=\{V_{1},\ldots ,V_{k}\}$ av $V(G)$ är inte $\varepsilon$ -regular, då finns det en förfining ${\mathcal {Q}}$ av ${\mathcal { P}}$ där varje $V_{i}$ är uppdelad i högst $2^{k}$ delar så att

$q({\mathcal {Q}})\geq q({\mathcal {P}})+\varepsilon ^{5}.$

Bevis: För alla $(i,j)$ så att $(V_{i},V_{j})$ inte är $\varepsilon$ -regular, hitta $A^{i,j}\subset V_{i}$ och $A^{j,i}\subset V_ {j}$ som bevittnar oegentligheter (gör detta samtidigt för alla oregelbundna par). Låt ${\mathcal {Q}}$ vara en vanlig förfining av ${\mathcal {P}}$$A^{i,j}$ A s. Varje $V_{i}$ är uppdelad i högst $2^{k}$ delar enligt önskemål. Sedan,

$q({\mathcal {Q}})=\summa _{(i,j)\in [k]^ {2}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})=\summa _{(V_{i},V_{j }){\text{ }}\varepsilon {\text{-regular}}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}} )+\summa _{(V_{i},V_{j}){\text{ inte }}\varepsilon {\text{-regular}}}q({\mathcal {Q}}_{V_{i} },{\mathcal {Q}}_{V_{j}})$

Där ${\mathcal {Q}}_{V_{i}}$ är partitionen av $V_{i}$ som ges av ${\mathcal {Q}}$ . Vid Lemma 1 är ovanstående kvantitet minst

$\sum _{(V_{i},V_{j}){\text{ }}\varepsilon {\text{-regular}}}q (V_{i},V_{j})+\summa _{(V_{i},V_{j}){\text{ inte }}\varepsilon {\text{-regular}}}q(\{A ^{i,j},V_{i}\backslash A^{i,j}\},\{A^{j,i},V_{j}\backslash A^{j,i}\})$

Eftersom $V_{i}$ skärs av $A^{i,j}$ när ${\displaystyle {\mathcal {Q}}} skapas$ , så ${\ displaystyle {\mathcal {Q}}_{V_{i}}}$ är en förfining av $\{A^{i,j},V_{i }\omvänt snedstreck A^{i,j}\}$ . Vid lemma 2 är summan ovan minst

$\sum _{(i,j)\in [k]^{2}}q(V_{i},V_{j})+\summa _{(V_{i},V_{j }){\text{ inte }}\varepsilon {\text{-regular}}}\varepsilon ^{4}{\frac {|V_{i}||V_{j}|}{n^{2}} }$

Men den andra summan är minst $\varepsilon ^{5}$ eftersom ${\mathcal {P}}$ inte är $\varepsilon$ -regelbunden, så vi härleder den önskade olikheten . $\square$

Nu, från vilken partition som helst, kan vi fortsätta att tillämpa Lemma 3 så länge som den resulterande partitionen inte är $\varepsilon$ -regular. Men i varje steg ökar energin med ${\displaystyle \varepsilon ^{5}} ,$ och den begränsas ovan av 1. Då kan denna process upprepas som mest $\varepsilon ^{-5}$ gånger , innan den avslutas och vi måste ha en $\varepsilon$ -vanlig partition.

Ansökningar

Lemma för grafräkning

Om vi ​​har tillräckligt med information om en grafs regelbundenhet kan vi räkna antalet kopior av en specifik subgraf i grafen upp till små fel.

Grafräkning Lemma. Låt $H$ vara en graf med ${\displaystyle V(H)=[k]} ,$ och låt $\varepsilon >0$ . Låt $G$ vara en $n$ -vertexgraf med vertexuppsättningar $V_{1},\dots ,V_{k}\subseteq V(G)$ så att $(V_{i},V_{j})$ är $\varepsilon$ -regular närhelst $\{i,j\}\in E(H)$ . Sedan är antalet märkta kopior av $H$ i $G$ inom $e(H)\varepsilon |V_{1}|\cdots |V_{k}|$ av

$\left(\prod _{\{i,j\}\in E(H)}d(V_{i},V_{j})\right)\left(\prod _{i=1} ^{k}|V_{i}|\höger).$

Detta kan kombineras med Szemerédis regularitetslemma för att bevisa Graph-borttagningslemma . Grafborttagningslemma kan användas för att bevisa Roths sats om aritmetiska progressioner , och en generalisering av det, hypergrafborttagningslemma, kan användas för att bevisa Szemerédis sats .

Lemmat för borttagning av grafer generaliserar till inducerade subgrafer genom att överväga kantredigeringar istället för endast kantborttagningar. Detta bevisades av Alon, Fischer, Krivelevich och Szegedy 2000. Detta krävde dock en starkare variation av regularitetslemma.

Szemerédis regularitetslemma ger inte meningsfulla resultat i glesa grafer . Eftersom glesa grafer har subkonstanta kantdensiteter, $\varepsilon$ -regelbundenhet trivialt tillfredsställt. Även om resultatet verkar rent teoretiskt, har vissa försök gjorts att använda regularitetsmetoden som komprimeringsteknik för stora grafer.

Fris-Kannan regelbundenhet

Ett annat begrepp om regularitet introducerades av Frieze och Kannan, känt som det svaga regelbundet lemma. Detta lemma definierar en svagare uppfattning om regelbundenhet än den för Szemerédi som använder bättre gränser och kan användas i effektiva algoritmer.

Givet en graf $G=(V,E)$ , en partition av dess hörn ${\mathcal {P}}=\ {V_{1},\ldots ,V_{k}\}$ sägs vara Frieze-Kannan $\epsilon$ -regular om för något par av uppsättningar $S,T\ subseteq V$ :

$\left|e(S,T)-\sum _{i,j=1}^{k}d(V_{i},V_{j})|S\cap V_{i}|| T\cap V_{j}|\right|\leq \epsilon |V|^{2}$

Det svaga regularitetslemma för grafer anger att varje graf har en svag $\epsilon$ -regular partition i högst $4^{\epsilon ^{-2}}$ delar.

Detta begrepp kan utvidgas till grafoner genom att definiera en stegoperator. Givet ett grafon $W$ och en partition ${\mathcal {P}}$ av $[0,1]$ , kan vi definiera $W_{\ mathcal {P}}$ som ett steggrafon med steg givna av ${\mathcal {P}}$ och värden givna genom att medelvärdet beräknas av $W$ över varje steg.

En partition ${\mathcal {P}}$ är svag $\epsilon$ -regular om:

$\|W-W_{\mathcal {P}}\|_{\square }\leq \epsilon$

Det svaga regularitetslemma för grafoner anger att varje grafon har en svag $\epsilon$ -regular partition i högst $4^{\epsilon ^{-2}}$ delar. Liksom med Szemerédis regularitetslemma framkallar den svaga regulariteten också ett räknelemmat.

Algoritmiska applikationer

En av de första motiven för utvecklingen av det svaga regularitetslemma var sökandet efter en effektiv algoritm för att uppskatta det maximala skäret i en tät graf . Det har visat sig att approximering av max-cut-problemet bortom 16/17 är NP-hårt , men en algoritmisk version av det svaga regularitetslemma ger en effektiv algoritm för att approximera max-cut-problemet för täta grafer inom en $\epsilon n^{2}$ additivfel. Dessa idéer har vidareutvecklats till effektiva samplingsalgoritmer för att uppskatta maxsnitt i täta grafer.

De mindre gränserna för det svaga regularitetslemma möjliggör effektiva algoritmer för att hitta en $\epsilon$ -regelbunden partition. Diagramregularitet har vidare använts inom olika områden av teoretisk datavetenskap , såsom matrismultiplikation och kommunikationskomplexitet .

Stark regelbundenhet lemma

Det starka regularitetslemmat är en starkare variant av det regularitetslemma som bevisades av Alon , Fischer, Krivelevich och Szegedy 2000. Intuitivt tillhandahåller det information mellan icke-regelbundna par och kan användas för att bevisa det inducerade grafborttagningslemma .

Påstående

För varje oändlig sekvens av konstanter ${\displaystyle \epsilon _{0}\geq \epsilon _{1}\geq ...>0} ,$ det finns ett heltal $M$ så att för vilken graf ${\displaystyle G} som helst$ , vi kan erhålla två (likvärdiga) partitioner ${\mathcal {P}}$ och ${\mathcal {Q}}$ så att följande egenskaper är uppfyllda:

• ${\mathcal {Q}}$ förfinar ${\mathcal {P}}$ , det vill säga varje del av ${\mathcal {P}}$ är föreningen av någon samling av delar i ${\mathcal {Q}}$ .
• ${\mathcal {P}}$ är $\epsilon _{0}$ -regular och ${\mathcal {Q}}$ är $\epsilon _{|{\mathcal {P}}|}$ -regelbunden.
• $q({\mathcal {Q}})<q({\mathcal {P}})+\epsilon _{0}$
• $|{\mathcal {Q}}|\leq M$

Bevis

Vi tillämpar regelbundet lemma upprepade gånger för att bevisa den starkare versionen. En grov översikt:

• Börja med ${\mathcal {P}}_{0}$ var en $\epsilon _{0}$ vanlig partition

• Hitta upprepade gånger dess förfining ${\mathcal {Q}}$ som är $\epsilon _{|{\mathcal {P}}|}$ regelbunden. Om energiökningen för ${\mathcal {Q}}\leq \epsilon _{0}$ returnerar vi helt enkelt $({\mathcal {P}},{\ mathcal {Q}})$ . Annars ersätter vi ${\mathcal {P}}$ med ${\mathcal {Q}}$ och fortsätter.

Vi börjar med ${\mathcal {P}}_{0}$ vara en $\epsilon _{0}$ vanlig partition av $G$ med $\leq M(\epsilon _{0})$ delar. Här $M(t)$ gränsen för delar i regularitetslemma när $\epsilon =t$ .

Nu för $i=0,1,\cdots$ ställer vi in ${\mathcal {P_{i+1}}}$ till en $\epsilon _{|P_{i}|}$ regelbunden förfining av ${\mathcal {P_{i}}}$ med ${\displaystyle \leq M(\epsilon _{|P_{i}|})|{\mathcal {P}}_{i}|} delar$ . Med energiökningsargumentet, $\displaystyle q({\mathcal {P}}_{i+1})\geq q({\mathcal {P}}$ . Eftersom energin är begränsad i $[0,1]$ måste det finnas några $i\leq 1/\epsilon _{0}+1$ så att $q({\mathcal {P}}_{i+1})-q({\mathcal {P}}_{i$ . Vi returnerar $({\mathcal {P}}_{i},{\mathcal {P}}_{i+1})$ som ${\ displaystyle ({\mathcal {P}},{\mathcal {Q}})}$ .

Genom vårt val av ${\mathcal {P}}_{i+1},$ gäller de vanliga och förfiningsvillkoren. Energitillståndet håller trivialt. Nu argumenterar vi för antalet delar. Vi använder induktion för att visa att $\forall i$ , det finns $M_{i}$ så att $|{\mathcal {P}}_{i}|\leq M_{i}$ . Genom att sätta $M_{0}=M(\epsilon _{0})$ har vi $|{\mathcal {P}}_{0}|\leq M_{0}$ . Observera att när $|P_{i}|\leq M_{i}$ , ${\displaystyle |P_{i+1}|\leq M(\epsilon _{|P_{i}|})|{\mathcal {P}}_{i} |\leq M(\epsilon _{|M_{i}|})M_{i}} ,$ så vi skulle kunna sätta $M_{i+1 }=M(\epsilon _{|M_{i}|})M_{i}$ och påståendet är sant för $i+1$ . Genom att sätta $M=\max _{i\leq 1/\epsilon _{0}+2}M_{i}$ har vi $|P|,|Q|\leq M.$

Anmärkningar om rättvisa

En partition är rättvis om storleken på två uppsättningar skiljer sig åt med högst $1$ . Genom att jämställa i varje omgång av iteration kunde beviset på regularitetslemma användas för att bevisa den rättvisa versionen av regularitetslemma. Och genom att ersätta regularitetslemma med dess rättvisa version, kan beviset ovan bevisa den rättvisa versionen av starkt regularitetslemma där ${\mathcal {P}}$ och ${\mathcal {Q}}$ är rättvisa partitioner.

En användbar följd

Påstående

För varje oändlig sekvens av konstanter ${\displaystyle \epsilon _{0}\geq \epsilon _{1}\geq ...>0} ,$ det finns $\delta >0$ så att det finns en partition ${\mathcal {P}}={V_{1},...,V_{k}}$ och delmängder $W_{i}\subset V_{i}$ för varje $i$ där följande egenskaper är uppfyllda:

• $|W_{i}|>\delta n$
• $(W_{i},W_{j})$ är $\epsilon _{|{\mathcal {P}}|}$ -regelbundet för varje par $1\leq i\leq j\leq k$
• $|d(W_{i},W_{j})-d(V_{i},V_{j})|\leq \epsilon _{0}$ för alla utom $\epsilon _{0}|{\mathcal {P}}|^{2}$ par $1\leq i\leq j\leq k$

Motivering

Följden utforskar djupare det lilla energitillskottet. Det ger oss en partition tillsammans med delmängder med stora storlekar från varje del, som är parvis regelbundna. Dessutom skiljer sig tätheten mellan motsvarande delmängdspar "inte mycket" från densiteten mellan motsvarande delar.

Bevis på följd

Vi kommer bara att bevisa det svagare resultatet där det andra villkoret endast kräver att $\epsilon _{|{\mathcal {P}}|}$$\displaystyle (W_{i},W_{j})}$ är -regular för $1\leq i<j\leq k$ . Den fullständiga versionen kan bevisas genom att välja fler delmängder från varje del som oftast är parvis regelbundna och kombinera dem.

Låt ${\displaystyle r=\epsilon _{0}^{3}/$ . Vi tillämpar det starka regularitetslemma för att hitta rättvis ${\mathcal {P}}$ som är en $r$ vanlig partition och rättvis ${\mathcal {Q}}$ som är en $r/|P|^{4}$ regelbunden förfining av ${\mathcal {P}}$ , så att $q({\ mathcal {Q}})-q({\mathcal {P}})\leq r$ och $|{\mathcal {Q}}|\leq M$ .

Antag nu att $P=\{V_{1},\cdots ,V_{k}\}$ , vi väljer slumpmässigt en vertex $v_{i }$ från varje $V_{i}$ och låt $W_{i}$ vara uppsättningen som innehåller $v_{i}$ i ${\mathcal {Q}}$ . Vi hävdar att delmängderna $W_{i}$ uppfyller alla villkor med sannolikhet $>0$ .

Genom att sätta $\delta ={\frac {1}{2M}}$ är det första villkoret trivialt sant eftersom ${\mathcal {Q}}$ är en rättvis partition. Eftersom högst ${\frac {r}{|P|^{4}}}{\binom {n}{2}}\leq \epsilon _{0}{\frac {|V_{i}||V_ {j}|}{3|P|^{2}}}$ vertexpar lever mellan oregelbundna par i ${\mathcal {Q}}$ , sannolikheten att paret $W_{i }$ och $W_{j}$ är oregelbunden $3|P|^{2}}}}$${$ , unionsbunden, sannolikheten att minst ett par $W_{i}$ , $\displaystyle W_{i}}$ är oregelbunden $1/3}$ leq Anteckna det

${\begin{aligned}r&\geq q({\mathcal {Q}})-q({\mathcal {P}})\\&=\sum _{i,j}{\frac { |V_{i}||V_{j}|}{n^{2}}}\mathbb {E} |d(W_{i},W_{j})-d(V_{i},V_{j })|^{2}\\&\geq \sum _{i,j}{\frac {1}{4|P|^{2}}}\mathbb {E} |d(W_{i}, W_{j})-d(V_{i},V_{j})|^{2}\\&={\frac {1}{4|P|^{2}}}\mathbb {E} \ summa _{i,j}|d(W_{i},W_{j})-d(V_{i},V_{j})|^{2}\end{aligned}}$

Så genom Markovs olikhet ${\displaystyle P(\sum$ , alltså med sannolikhet $\geq 1/2$ , högst $\epsilon _{0}|P|^{2}$ par kan ha $W_{i}, W_{j})-d(V_{i},V_{j})\geq \epsilon _{0}}$ . Genom unionsbunden, sannolikheten att alla villkor håller $\geq 1-1/2-1/3>0$ .

Historik och tillägg

Gowers konstruktion för den nedre gränsen av Szemerédis regularitetslemma

Szemerédi (1975) introducerade först en svagare version av detta lemma, begränsad till tvådelade grafer, för att bevisa Szemerédis teorem , och i ( Szemerédi 1978 ) bevisade han hela lemmat. Utvidgningar av regularitetsmetoden till hypergrafer erhölls av Rödl och hans medarbetare och Gowers .

János Komlós , Gábor Sárközy och Endre Szemerédi bevisade senare (1997) i uppblåsningslemmat att de reguljära paren i Szemerédi regularitetslemma beter sig som kompletta tvådelade grafer under de korrekta förhållandena. Lemmat möjliggjorde djupare utforskning av karaktären av inbäddningar av stora glesa grafer till täta grafer.

Den första konstruktiva versionen kom från Alon, Duke, Lefmann, Rödl och Yuster. Därefter Frieze och Kannan en annan version och utökade den till hypergrafer. De producerade senare en annan konstruktion på grund av Alan Frieze och Ravi Kannan som använder singulära värden av matriser. Man kan hitta mer effektiva icke-deterministiska algoritmer, som formellt beskrivs i Terence Taos blogg och implicit nämns i olika tidningar.

En ojämlikhet av Terence Tao utökar Szemerédi regelbundenhet lemma, genom att se över det från perspektivet av sannolikhetsteorin och informationsteorin istället för grafteorin. Terence Tao har också gett ett bevis på lemma baserat på spektral teori, med hjälp av närliggande matriser av grafer.

Det är inte möjligt att bevisa en variant av regularitetslemma där alla par av partitionsuppsättningar är regelbundna. Vissa grafer, som de halva graferna , kräver att många par av partitioner (men en liten del av alla par) är oregelbundna.

Det är en vanlig variant i definitionen av en $\varepsilon$ -vanlig partition att kräva att vertexuppsättningarna alla har samma storlek, samtidigt som man samlar de överblivna hörnen i en "error"-set $V_{ 0}$ vars storlek är högst en $\varepsilon$ -fraktion av storleken på vertexuppsättningen av $G$ .

En starkare variation av regularitetslemma bevisades av Alon, Fischer, Krivelevich och Szegedy samtidigt som det inducerade grafborttagningslemma bevisades. Detta fungerar med en sekvens av $\varepsilon$ istället för bara en, och visar att det finns en partition med en extremt regelbunden förfining, där förfiningen inte har ett för stort energiökning.

Szemerédis regularitetslemma kan tolkas som att utrymmet för alla grafer är totalt avgränsat (och därmed prekompakt ) i en lämplig metrik (avsnittsavståndet ) . Gränser i detta mått kan representeras av grafoner ; en annan version av regularitetslemma säger helt enkelt att grafonernas utrymme är kompakt .

Vidare läsning

•   Komlós, J. ; Simonovits, M. (1996), "Szemerédis regularitetslemma och dess tillämpningar i grafteori", Combinatorics, Paul Erdős är åttio, Vol. 2 (Keszthely, 1993) , Bolyai Soc. Matematik. Stud., vol. 2, János Bolyai Math. Soc., Budapest, s. 295–352, MR 1395865 .
•    Komlós, J. ; Shokoufandeh, Ali; Simonovits, Miklós ; Szemerédi, Endre (2002), "The regularity lemma and its applications in graph theory", Theoretical aspects of data science (Tehran, 2000) , Lecture Notes in Computer Science , vol. 2292, Springer, Berlin, s. 84–112, doi : 10.1007/3-540-45878-6_3 , ISBN 978-3-540-43328-6 , MR 1966181 .

externa länkar

• Edmonds, Chelsea; Koutsoukou-Argyraki, Angeliki; Paulson, Lawrence C. Szemerédis regularitetslemma (Formell bevisutveckling i Isabelle/HOL, Archive of Formal Proofs)