Suurballes algoritm

Inom teoretisk datavetenskap och nätverksrouting är Suurballes algoritm en algoritm för att hitta två disjunkta vägar i en icke-negativt viktad riktad graf , så att båda vägarna förbinder samma par av hörn och har minsta totala längd. Algoritmen skapades av John W. Suurballe och publicerades 1974. Huvudidén med Suurballes algoritm är att använda Dijkstras algoritm för att hitta en väg, för att modifiera grafkanternas vikter och sedan köra Dijkstras algoritm en andra gång. Algoritmens utdata bildas genom att kombinera dessa två vägar, kasta kanter som korsas i motsatta riktningar av banorna och använda de återstående kanterna för att bilda de två vägarna för att återvända som utdata. Ändringen av vikterna liknar viktändringen i Johnsons algoritm och bevarar vikternas icke-negativitet samtidigt som den andra instansen av Dijkstras algoritm kan hitta den korrekta andra vägen.

Problemet med att hitta två disjunkta banor med minimivikt kan ses som ett specialfall av ett minimikostnadsflödesproblem , där det i detta fall finns två enheter av "flöde" och noder har enhets "kapacitet". Suurballes algoritm kan också ses som ett specialfall av en minimikostnadsflödesalgoritm som upprepade gånger pressar maximalt möjliga mängd flöde längs en kortaste förstärkningsväg. Den första vägen som hittas av Suurballes algoritm är den kortaste förstärkningsvägen för det initiala (noll) flödet, och den andra vägen som hittas av Suurballes algoritm är den kortaste förstärkningsvägen för restgrafen som finns kvar efter att ha drivit en flödesenhet längs den första banan .

Definitioner

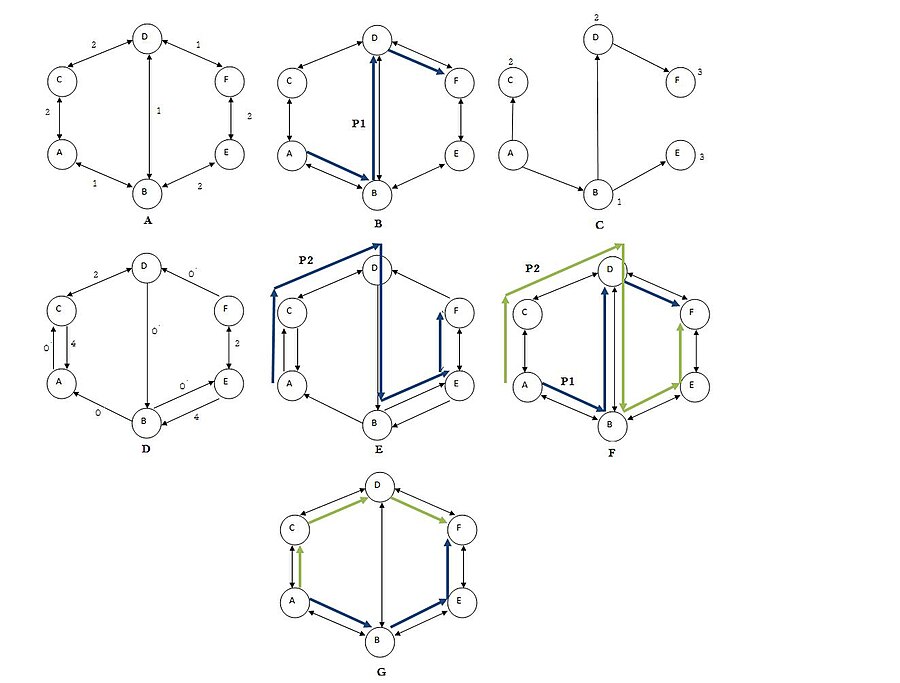
Låt G vara en vägd riktad graf med vertexuppsättning V och kantmängd E (figur A); låt s vara en designad källpunkt i G och låt t vara en designad destinationspunkt. Låt varje kant ( u , v ) i E , från vertex u till vertex v , ha en icke-negativ kostnad w ( u , v ) .

Definiera s d( s , u ) för att vara kostnaden för den kortaste vägen till vertex u från vertex s i det kortaste vägträdet med rötter vid ( figur C).

Obs: Nod och Vertex används ofta omväxlande.

Algoritm

Suurballes algoritm utför följande steg:

1. Hitta det kortaste vägträdet T som är rotat vid nod s genom att köra Dijkstras algoritm (figur C). Detta träd innehåller för varje vertex u , en kortaste väg från s till u . Låt P ₁ vara den kortaste kostnadsvägen från s till t (figur B). Kanterna i T kallas trädkanter och de återstående kanterna (kanterna som saknas i figur C) kallas icke-trädkanter .
2. 
   
   Ändra kostnaden för varje kant i grafen genom att ersätta kostnaden w ( u , v ) för varje kant ( u , v ) med w′ ( u , v ) = w ( u , v ) − d( s , v ) + d( s , u ) . Enligt den resulterande modifierade kostnadsfunktionen har alla trädkanter en kostnad på 0, och icke-trädkanter har en icke-negativ kostnad. Till exempel: Om u =B, v =E , då w′ ( u , v ) = w (B,E) − d(A,E) + d(A,B) = 2 − 3 + 1 = 0 Om u =E, v =B , sedan w′ ( u , v ) = w (E,B) − d(A,B) + d(A,E) = 2 − 1 + 3 = 4
3. Skapa en restgraf G _t bildad från G genom att ta bort kanterna på G på banan P ₁ som är riktade in i s och vänd sedan riktningen för nolllängdskanterna längs banan P ₁ (figur D).
4. Hitta den kortaste vägen P ₂ i restgrafen G _t genom att köra Dijkstras algoritm (figur E).
5. Kassera de omvända kanterna av P ₂ från båda banorna. De återstående kanterna av P ₁ och P ₂ bildar en subgraf med två utgående kanter vid s , två inkommande kanter vid t , och en inkommande och en utgående kant vid varje återstående vertex. Därför består denna subgraf av två kantuppdelade banor från s till t och möjligen några ytterligare (noll-längd) cykler. Returnera de två disjunkta banorna från subgrafen.

Exempel

Följande exempel visar hur Suurballes algoritm hittar det kortaste paret av disjunkta vägar från A till F .

Figur A illustrerar en viktad graf G.

Figur B beräknar den kortaste vägen P ₁ från A till F ( A – B – D – F ).

Figur C illustrerar det kortaste vägträdet T med rötter vid A och de beräknade avstånden från A till varje vertex ( u ).

Figur D visar restgrafen Gt _banan med den uppdaterade kostnaden för varje kant och kanterna på Pi _omvända .

Figur E beräknar väg P ₂ i restgrafen G _t ( A – C – D – B – E – F ).

Figur F illustrerar både _väg Pi och väg P2 _.

Figur G hittar det kortaste paret av osammanhängande banor genom att kombinera kanterna på banorna P ₁ och P ₂ och sedan kassera de gemensamma omvända kanterna mellan båda banorna ( B – D ). Som ett resultat får vi de två kortaste paren av disjunkta banor ( A – B – E – F ) och ( A – C – D – F ).

Rätthet

Vikten av en bana från s till t i det modifierade d( s , t ) systemet av vikter är lika med vikten i den ursprungliga grafen, minus . Därför är de två kortaste osammanhängande vägarna under de modifierade vikterna samma vägar som de två kortaste vägarna i den ursprungliga grafen, även om de har olika vikt.

Suurballes algoritm kan ses som ett specialfall av den successiva kortaste vägsmetoden för att hitta ett minimikostnadsflöde med totalt flödesbelopp två från s till t . Ändringen av vikterna påverkar inte sekvensen av vägar som hittas med denna metod, bara deras vikter. Därför följer algoritmens korrekthet av korrektheten hos den successiva metoden med kortaste vägar.

Analys och gångtid

Denna algoritm kräver två iterationer av Dijkstras algoritm. Med hjälp av Fibonacci-högar kan båda iterationerna utföras i tiden $O(|E|+|V|\log |V|)$ där $|V|$ och $|E|$ är antalet hörn respektive kanter. Därför gäller samma tidsgräns för Suurballes algoritm.

Variationer

Den version av Suurballes algoritm som beskrivs ovan hittar vägar som har disjunkta kanter, men som kan dela hörn. Det är möjligt att använda samma algoritm för att hitta spets-disjunkta banor, genom att ersätta varje vertex med ett par angränsande hörn, en med alla inkommande angränsningar u-in av den ursprungliga vinkeln och en med alla utgående angränsande punkter u -ut . Två kantuppdelade banor i den här modifierade grafen motsvarar nödvändigtvis två spetsuppdelade banor i den ursprungliga grafen, och vice versa, så att tillämpa Suurballes algoritm på den modifierade grafen resulterar i konstruktionen av två spetsuppdelade banor i den ursprungliga grafen. Suurballes ursprungliga algoritm från 1974 gällde versionen av problemet med hörn-disjunkt och utökades 1984 av Suurballe och Tarjan till versionen med kant-disjunkt.

Genom att använda en modifierad version av Dijkstras algoritm som samtidigt beräknar avstånden till varje vertex t i graferna G _t , är det också möjligt att hitta de totala längderna av de kortaste paren av vägar från en given källpunkt s till varannan vertex i graf, i en tidsperiod som är proportionell mot en enda instans av Dijkstras algoritm.

Notera: Paret av intilliggande hörn som härrör från uppdelningen är sammankopplade med en enkelriktad kant som kostar noll från den inkommande till utgående hörn. Källpunkten blir s-out och destinationspunkten blir t-in .

Se även

• Edge disjunkt kortaste par algoritm