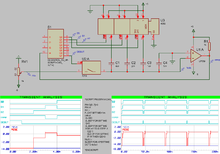
Successiv approximation ADC

För beteendepsykolog BF Skinners metod för att vägleda inlärt beteende, se Shaping (psykologi) . För successiv approximation i allmänhet, se Successiv approximation .

Successiv approximation ADC-blockdiagram som visar digital-till-analog-omvandlare (DAC), slutet av konverteringsindikator (EOC), successiv approximationsregister (SAR), samplings- och hållkrets (S/H), ingångsspänning (Vin ₎ och referens spänning ( V _ref )

En successiv approximations-ADC är en typ av analog-till-digital-omvandlare som omvandlar en kontinuerlig analog vågform till en diskret digital representation med hjälp av en binär sökning genom alla möjliga kvantiseringsnivåer innan den slutligen konvergerar till en digital utgång för varje konvertering.

Algoritm

Den successiva tillnärmningskretsen för analog-till-digital-omvandlare består vanligtvis av fyra huvuddelkretsar:

1. En samplings-och-håll- krets för att få in inspänningen V _in .
2. En analog spänningskomparator som jämför V _in med utgången från den interna DAC:n och matar ut resultatet av jämförelsen till successive approximationsregistret ( SAR ).
3. En registerunderkrets för successiv approximation utformad för att leverera en ungefärlig digital kod av V _in till den interna DAC:n.
4. En intern referens-DAC som, för jämförelse med V _ref , förser komparatorn med en analog spänning lika med den digitala kodutgången från SAR _i .

Animation av en 4-bitars successiv approximation ADC

Det successiva approximationsregistret initieras så att den mest signifikanta biten (MSB) är lika med en digital 1. Denna _kod Vref / 2) matas in i DAC:n, som sedan matar den analoga motsvarigheten till denna digitala kod ( till komparatorkretsen för jämförelse med den samplade inspänningen. Om denna analoga spänning överstiger _Vin , får komparatorn SAR att återställa denna bit; annars lämnas biten som 1. Sedan sätts nästa bit till 1 och samma test görs, och fortsätter denna binära sökning tills varje bit i SAR har testats. Den resulterande koden är den digitala approximationen av den samplade inspänningen och matas slutligen ut av SAR vid slutet av konverteringen (EOC).

Matematiskt, låt V _in = xV _ref , så x i [−1, 1] är den normaliserade inspänningen. Målet är att ungefär digitalisera på 1⁄2 x ⁿ med en noggrannhet . Algoritmen fortsätter enligt följande:

1. Initial approximation ₀ x = 0 .
2. i: ^e approximationen x _i = x _{i −1} − s ( x _{i −1} − x )/2 ⁱ , där s ( x ) är signumfunktionen ( sgn( x ) = +1 för x ≥ 0 , −1 för x < 0 ). Det följer med hjälp av matematisk induktion att | x _n − x | ≤ 1/2 ⁿ .

Som visas i ovanstående algoritm kräver en SAR ADC:

1. En inspänningskälla V _in .
2. En referensspänningskälla Vref _. för att normalisera ingången
3. En DAC för att omvandla den i: ^te approximationen x _i till en spänning.
4. En komparator för att utföra funktionen s ( x _i − x ) genom att jämföra DAC:ns spänning med ingångsspänningen.
5. Ett register för att lagra utgången från komparatorn och applicera x _{i −1} − s ( x _{i −1} − x )/2 ⁱ .

Drift av successiv approximation ADC som inspänning faller från 5 till 0 V. Iterationer på x -axeln. Approximationsvärde på y- axeln.

Exempel: De tio stegen för att konvertera en analog ingång till 10 bitars digital, med successiv approximation, visas här för alla spänningar från 5 V till 0 V i 0,1 V iterationer. Eftersom referensspänningen är 5 V, när ingångsspänningen också är 5 V, är alla bitar inställda. När spänningen sänks till 4,9 V rensas bara några av de minst signifikanta bitarna. MSB förblir inställd tills ingången är hälften av referensspänningen, 2,5 V.

De binära vikterna som tilldelas varje bit, som börjar med MSB, är 2,5, 1,25, 0,625, 0,3125, 0,15625, 0,078125, 0,0390625, 0,01953125, 0,0059760, 8,204, 8,204, 8. Alla dessa summerar till 4,9951171875, vilket betyder binär 1111111111, eller en LSB mindre än 5.

När den analoga ingången jämförs med den interna DAC-utgången jämförs den effektivt med var och en av dessa binära vikter, med början på 2,5 V och antingen behåller den eller rensar den som ett resultat. Genom att sedan addera nästa vikt till föregående resultat, jämföra igen och upprepa tills alla bitar och deras vikter har jämförts med ingången, hittas slutresultatet, ett binärt tal som representerar den analoga ingången.

Varianter

• Räknartyp ADC: D till A-omvandlaren kan enkelt vridas runt för att ge den omvända funktionen A till D-omvandling. Principen är att justera DAC:s ingångskod tills DAC:ns utgång kommer inom ± 1 ⁄ 2 LSB till den analoga ingången som ska konverteras till binär digital form.
• Servo tracking ADC: Det är en förbättrad version av en counting ADC. Kretsen består av en upp-ned-räknare med komparatorn som styr räkneriktningen. DAC:ns analoga utgång jämförs med den analoga ingången. Om ingången är större än DAC-utgångssignalen, blir utgången från komparatorn hög och räknaren bringas att räkna upp. Spårnings-ADC har fördelen att vara enkel. Nackdelen är dock den tid som behövs för att stabiliseras eftersom ett nytt omvandlingsvärde är direkt proportionell mot den hastighet med vilken den analoga signalen ändras.

Laddnings-omfördelning successiv approximation ADC

Laddningsskalande DAC

En av de vanligaste implementeringarna av successiv approximation ADC, laddnings-omfördelning successiv approximation ADC, använder en laddningsskalande DAC . Laddningsskalande DAC består helt enkelt av en rad individuellt kopplade binärt vägda kondensatorer. Mängden laddning på varje kondensator i arrayen används för att utföra den tidigare nämnda binära sökningen i samband med en komparator internt i DAC:n och det successiva approximationsregistret.

3-bitars simulering av en kapacitiv ADC

1. Kondensatoruppsättningen är fullständigt urladdad till komparatorns offsetspänning _, VOS . Detta steg ger automatisk offset-annullering (dvs. offsetspänningen representerar inget annat än dödladdning, som inte kan jongleras av kondensatorerna).
2. Alla kondensatorer inom arrayen kopplas om till ingångssignalen V _in . Kondensatorerna har nu en laddning lika med deras respektive kapacitans gånger ingångsspänningen minus offsetspänningen på var och en av dem.
3. Kondensatorerna växlas sedan så att denna laddning appliceras över komparatoringången, vilket skapar en komparatoringångsspänning lika med − V _in .
4. Själva konverteringsprocessen fortsätter. Först kopplas MSB-kondensatorn om till Vref _, vilket motsvarar fullskaleområdet för ADC. På grund av den binära viktningen av arrayen bildar MSB-kondensatorn en 1:1 laddningsdelare med resten av arrayen. Således är inspänningen till komparatorn nu − V _in + V _ref ⁄ 2 . Därefter Vref _, ⁄ 2 om Vin _. är större än , matar komparatorn en digital 1 som MSB, annars matar den ut en digital 0 som MSB Varje kondensator testas på samma sätt tills komparatorns inspänning konvergerar till offsetspänningen, eller åtminstone så nära som möjligt givet DAC:ns upplösning.

Använd med icke-ideala analoga kretsar

När den implementeras som en analog krets – där värdet för varje successiv bit inte är perfekt 2 ^N (t.ex. 1.1, 2.12, 4.05, 8.01, etc.) – kanske en successiv approximationsmetod inte matar ut det ideala värdet eftersom den binära sökalgoritmen är felaktigt tar bort vad den tror är hälften av de värden som den okända ingången inte kan vara. Beroende på skillnaden mellan faktisk och idealisk prestanda, kan det maximala felet lätt överstiga flera LSB:er, speciellt som felet mellan det faktiska och ideala 2N ^blir stort för en eller flera bitar. Eftersom den faktiska ingången är okänd är det därför mycket viktigt att noggrannheten hos den analoga kretsen som används för att implementera en SAR ADC är mycket nära de ideala 2 ^N -värdena; annars kan det inte garantera en bästa matchning.

Se även

• Kvantiseringsbrus
• Digital-till-analog omvandlare

Vidare läsning

•   CMOS-kretsdesign, layout och simulering, 3:e upplagan ; RJ Baker; Wiley-IEEE; 1208 sidor; 2010; ISBN 978-0-470-88132-3
•   Handbok för datakonvertering ; Analoga enheter; Newnes; 976 sidor; 2004; ISBN 978-0750678414

externa länkar

• Förstå SAR ADC:er: deras arkitektur och jämförelse med andra ADC:er - Maxim
• Välj rätt A/D-omvandlare för din applikation - TI