Strömordning

Bäckordningen eller vattenkroppsordningen är ett positivt heltal som används inom geomorfologi och hydrologi för att indikera nivån av förgrening i ett flodsystem .

Det finns olika tillvägagångssätt för den topologiska ordningen av floder eller sektioner av floder baserat på deras avstånd från källan ("top down") eller från sammanflödet ( punkten där två floder smälter samman) eller flodmynningen ("bottom up"), och deras hierarkiska position inom flodsystemet. Som terminologi tenderar orden "ström" och "gren" att användas snarare än "flod".

Klassisk streamordning

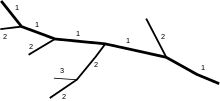
Den klassiska strömordningen , även kallad Hacks strömordning eller Gravelius strömordning , är en "bottom up"-hierarki som tilldelar siffran "1" till floden med dess mynning vid havet (huvudstammen ) . Strömordningen är en viktig aspekt av en dräneringsbassäng. Det definieras som måttet på en ströms position i hierarkin av strömmar. Bifloder ges ett nummer ett högre än det för floden eller bäcken i vilken de rinner ut. Så till exempel får alla omedelbara bifloder till huvudstammen numret "2". Bifloder som töms i en "2" får siffran "3" och så vidare.

Denna typ av bäckordning anger flodens plats i nätet. Den är lämplig för allmänna kartografiska ändamål, men kan ställa till problem eftersom det vid varje sammanflöde måste fattas ett beslut om vilken av de två grenarna som är en fortsättning på huvudkanalen, och om huvudkanalen har sin källa vid sammanflödet av två andra. mindre bäckar. Den första ordningens bäck är den som vid varje sammanflöde har det största volymetriska flödet, vilket vanligtvis återspeglar det långvariga namngivningen av floder. Förknippat med detta strömordningssystem var 1800-talets geografers strävan att hitta den "sanna" källan till en flod. Under arbetets gång diskuterades andra kriterier för att göra det möjligt att definiera huvudströmmen. Förutom att mäta flodernas längd (avståndet mellan den längsta källan och mynningen) och storleken på de olika avrinningsområdena , sökte geograferna efter den bäck som avvek minst vid det faktiska sammanflödet, samt tog hänsyn till de successiva namnen på floder och deras bifloder, såsom Rhen och Aare eller Elbe och Moldau .

Strahler stream order

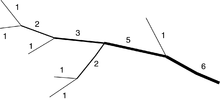
Enligt "top-down"-systemet som utarbetats av Strahler , är floder av första ordningen de yttersta bifloderna. Om två strömmar av samma ordning går samman, får den resulterande strömmen ett nummer som är ett högre. Om två floder med olika strömordningar går samman, ges den resulterande strömmen det högsta av de två talen.

Strahler-ordningen är utformad för att återspegla morfologin i ett avrinningsområde och utgör grunden för viktiga hydrografiska indikatorer på dess struktur, såsom dess bifurkationsförhållande, dräneringstäthet och frekvens. Dess grund är avrinningsområdets vattendelare . Det är dock skalberoende. Ju större kartskala , desto fler strömningsordningar kan avslöjas. En allmän nedre gräns för definitionen av en "ström" kan sättas genom att definiera dess bredd vid mynningen eller, med hänvisning till en karta, genom att begränsa dess utsträckning. Systemet i sig är även tillämpbart för andra småskaliga strukturer utanför hydrologi.

Shreve-strömningsordning

Shreve-systemet ger också de yttersta bifloderna siffran "1". Till skillnad från Strahler-metoden adderas de två talen vid ett sammanflöde.

Shreve-strömningsordning är att föredra inom hydrodynamik : den summerar antalet källor i varje avrinningsområde ovanför en strömmätare eller utflöde och korrelerar ungefär till utsläppsvolymerna och föroreningsnivåerna. Liksom Strahlermetoden är den beroende av precisionen hos de ingående källorna, men mindre beroende av kartskala. Den kan göras relativt skaloberoende genom att använda lämplig normalisering och är då i stort sett oberoende av en exakt kunskap om ett områdes övre och nedre lopp.

Horton och topologiska strömordningar

Andra system inkluderar Horton-strömningsordningen, ett tidigt uppifrån-och-ned-system utarbetat av Robert E. Horton , och det topologiska strömningsordersystemet, som är "ett bottom-up"-system, och där strömordningens nummer ökar med ett vid varje sammanflöde.

Jämförelse av klassisk strömordning med Horton- och Strahler-metoder

Klassiska eller topologiska ordningssystem tilldelas en dimensionslös numerisk ordning av "ett", med början vid mynningen av en bäck, som är dess lägsta höjdpunkt. Vektorordningen ökar sedan när den spårar uppströms och konvergerar med andra mindre strömmar, vilket resulterar i en korrelation av högre ordningens tal till mer högt upphöjda huvudvatten.

Horton föreslog att man skulle vända den ordningen. Hortons forskningsrapport från 1947 etablerade en strömordningsmetod baserad på vektorgeometri. 1952 Arthur Strahler en modifiering av Hortons metod. Både Hortons och Strahlers metoder etablerade tilldelningen av den lägsta ordningen, nummer 1, med början vid flodens huvudvatten, som är den högsta höjdpunkten. Klassisk ordernummertilldelning korrelerar med höjd och höjd och spår uppströms, men Horton och Strahlers strömordningsmetoder korrelerar med gravitationsflöde och spår nedströms.

Både Hortons och Strahlers strömordningsmetoder förlitar sig på principerna för vektorpunktlinjegeometri. Hortons och Strahlers regler utgör grunden för programmeringsalgoritmer som tolkar kartdata som efterfrågas av Geographic Information Systems .

Användande

Den klassiska användningen av strömordning är i allmänhet hydrologisk kartografi. Bäckordningssystem är också viktiga för en systematisk kartläggning av ett älvsystem, vilket möjliggör tydlig märkning och ordning av bäckar.

Strahler- och Shreve-metoderna är särskilt värdefulla för modellering och morfometrisk analys av flodsystem, eftersom de definierar varje sektion av en flod. Det gör att nätverket kan separeras vid varje spårvidd eller utflöde i uppströms- och nedströmsregimer, och för dessa punkter att klassificeras. Dessa system används också som underlag för modellering av vattenbudgeten med hjälp av lagringsmodeller eller tidsrelaterade, nederbörd-utflödesmodeller och liknande.

Inom den GIS-baserade geovetenskapen används dessa två modeller eftersom de visar den grafiska utsträckningen av ett flodobjekt.

Forskningsverksamheten efter Strahlers rapport från 1952 har fokuserat på att lösa vissa utmaningar när man konverterar tvådimensionella kartor till tredimensionella vektormodeller. En utmaning har varit att konvertera rastrerade pixelbilder av strömmar till vektorformat. Ett annat problem har varit att kartskalningsjusteringar vid användning av GIS kan ändra strömklassificeringen med en faktor eller en eller två beställningar. Beroende på GIS-kartans skala kan några fina detaljer av trädstrukturen i ett flodsystem gå förlorade.

Forskningsinsatser från privat industri, universitet och federala myndigheter som EPA och USGS har kombinerat resurser och anpassat fokus för att studera dessa och andra utmaningar. Den huvudsakliga avsikten är att standardisera programvara och programmeringsregler så att GIS-data är konsekvent tillförlitliga i alla kartskala. För detta ändamål har både EPA och USGS gått i spetsen för standardiseringsinsatser, som kulminerade i skapandet av The National Map . Både federala myndigheter såväl som ledande mjukvaruföretag inom den privata industrin har antagit Hortons och Strahlers strömordningsvektorprinciper som grund för kodningslogikregler inbyggda i den standardiserade National Map-mjukvaran.

Se även

Källor

Drwal, J. Wykształcenie i organizacja sieci hydrograficznej jako podstawa oceny struktury odpływu na terenach młodoglacjalnych, Rozprawy i monografie, Gdansk, 1982, 130 pp (på polska)
Hack, J. Studier av längsgående strömprofiler i Virginia och Maryland , US Geological Survey Professional Paper, 1957, 294-B
Horton, RE, Erosionsutveckling av bäckar och deras dräneringsbassänger: hydrofysisk syn på kvantitativ morfologi, Geological Society of America Bulletin 56 (3): 275-370, 1945
Koschitzki, Thomas. GIS-baserat, automatiskt Erfassung natürlicher Fließgewässerhierarchien och ihre Abbildung i Datenbanken, beispielhaft dargestellt am Einzugsgebiet der Salza. Avhandling, Martin-Luther-Universität Halle-Wittenberg, Halle (Saale), 2004, URN (NBN) urn:nbn:de:gbv:3-000007179 ( Webblänk , arkivserver DNB)
Scheidegger AE, (1966), Statistisk beskrivning av flodnät. Vattenresurs. Res., 2(4): 785-790
Shreve, R., (1966), Statistical Law of Stream Numbers, J. Geol., 74, 17-37.
Strahler, AN Dynamisk grund för geomorfologi. I: Geological Society of America Bulletin 63/1952, s. 923–938.
Strahler, AN Kvantitativ analys av vattendelars geomorfologi. Transaktioner från American Geophysical Union. 1957; 38(6), sid. 913-920.
Strahler, AN "Kvantitativ geomorfologi av dräneringsbassänger och kanalnätverk." Chow, VT, redaktör. Handbok för tillämpad hydrologi . New York: McGraw-Hill; 1964; sid. 4-39, 4-76.
Shreve, R. Statistisk lag för strömtal. I: Journal of Geology 74/1966.
Weishar, Lee L. Utveckling av Marsh Hydrogeomorphology and Marsh Vegetation with a Salt Hay Farm Wetland Restoration Site . Hämtad 16 april 2017.
Woldenberg, MJ, (1967), Geografi och egenskaper hos ytor, Harvard Papers in Theoretical Geography, 1: 95-189.
Rivertool – Tillägg för ArcView, användningsdokumentation, Office of Applied Hydrology ( Weblink , gis-tools.de)

externa länkar

International Glossary of Hydrology (pdf-fil; 1,24 MB)
"Gewässernetz: Stream Order Numbers for the Digitalized Water Network, 1:25 000 series, Switzerland" . Hydrologische Grundlagen und Daten – Informationssysteme und Methoden – Gewässernetz – Flussordnungszahlen ( på tyska). Bundesamt für Umwelt BAFU. 4 april 2007 . Hämtad 8 mars 2008 .