Stegdetektering
Inom statistik och signalbehandling är stegdetektering (även känd som stegutjämning , stegfiltrering , skiftdetektering , hoppdetektering eller kantdetektering ) processen att hitta abrupta förändringar (steg, hopp, skift) i medelnivån för en tidsserie eller signal. Det betraktas vanligtvis som ett specialfall av den statistiska metoden som kallas förändringsdetektering eller förändringspunktsdetektering. Ofta är steget litet och tidsserien är skadad av något slags brus , vilket gör problemet utmanande eftersom steget kan döljas av bruset. Därför krävs ofta statistiska och/eller signalbehandlingsalgoritmer.
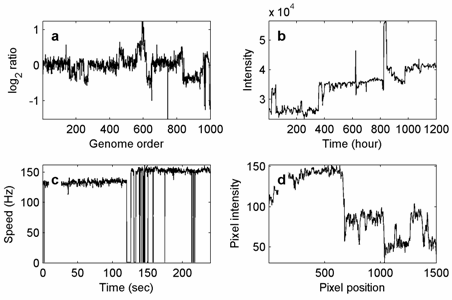
Stegdetekteringsproblemet uppstår i flera vetenskapliga och tekniska sammanhang, till exempel i statistisk processkontroll ( kontrolldiagrammet är den mest direkt relaterade metoden), inom utforskningsgeofysik ( där problemet är att segmentera en brunnsloggregistrering i stratigrafiska zoner ), i genetik (problemet med att separera mikroarraydata i liknande kopienummerregimer ) och i biofysik (upptäcka tillståndsövergångar i en molekylär maskin som registrerats i tidspositionsspår). För 2D-signaler har det relaterade problemet med kantdetektering studerats intensivt för bildbehandling .
Algoritmer
När stegdetekteringen måste utföras när och när data anländer, används vanligtvis onlinealgoritmer , och det blir ett specialfall av sekventiell analys . Sådana algoritmer inkluderar den klassiska CUSUM -metoden som tillämpas på förändringar i medelvärde.
Däremot tillämpas offlinealgoritmer på data potentiellt långt efter att de har tagits emot . De flesta offlinealgoritmer för stegdetektering i digital data kan kategoriseras som metoder uppifrån och ned , nedifrån och upp , glidande fönster eller globala metoder.
Uppifrån och ner
Dessa algoritmer börjar med antagandet att det inte finns några steg och introducerar möjliga kandidatsteg ett i taget, och testar varje kandidat för att hitta den som minimerar vissa kriterier (som minsta kvadraters anpassning av den uppskattade, underliggande bitvis konstanta signalen). Ett exempel är den stegvisa hoppplaceringsalgoritmen , som först studerades i geofysiska problem, som har funnit nya användningsområden inom modern biofysik.
Botten upp
Bottom-up-algoritmer tar det "motsatta" tillvägagångssättet till top-down-metoder, och antar först att det finns ett steg mellan varje sampel i den digitala signalen, och sedan successivt sammanslagning av steg baserat på några kriterier som testats för varje kandidatsammanslagning.
Glidande fönster
Genom att betrakta ett litet "fönster" av signalen letar dessa algoritmer efter bevis på att ett steg inträffar i fönstret. Fönstret "glider" över tidsserien, ett tidssteg i taget. Bevisen för ett steg testas med statistiska procedurer, till exempel genom att använda två-provet Students t-test . Alternativt appliceras ett olinjärt filter såsom medianfiltret på signalen. Filter som dessa försöker ta bort bruset samtidigt som de plötsliga stegen bevaras.
Global
Globala algoritmer överväger hela signalen på en gång och försöker hitta stegen i signalen genom någon form av optimeringsprocedur. Algoritmer inkluderar wavelet- metoder och total variation denoising som använder metoder från konvex optimering . Där stegen kan modelleras som en Markov-kedja , används också ofta Hidden Markov-modeller (ett populärt tillvägagångssätt inom biofysikgemenskapen). När det bara finns ett fåtal unika värden på medelvärdet, k-medelklustring också användas.
Linjära kontra olinjära signalbehandlingsmetoder för stegdetektering
Eftersom steg och (oberoende) brus har teoretiskt oändlig bandbredd och sålunda överlappar i Fourier-basen , använder signalbehandlingsmetoder för stegdetektering i allmänhet inte klassiska utjämningstekniker såsom lågpassfiltret . Istället är de flesta algoritmer uttryckligen olinjära eller tidsvarierande.
Stegdetektering och styckvis konstanta signaler
Eftersom syftet med stegdetektering är att hitta en serie momentana hopp i medelvärdet av en signal, är den önskade, underliggande medelsignalen konstant konstant . Av denna anledning kan stegdetektering lönsamt ses som problemet med att återställa en bitvis konstant signal som skadats av brus. Det finns två kompletterande modeller för styckvis konstanta signaler: som 0-graders splines med några få knop, eller som nivåuppsättningar med några unika nivåer. Många algoritmer för stegdetektering förstås därför bäst som antingen 0-graders splinepassning, eller nivåuppsättningsåterställningsmetoder.
Stegdetektering som återhämtning av nivåuppsättning
När det bara finns ett fåtal unika värden på medelvärdet, är klustringstekniker som k-medelvärden klustring eller medelförskjutning lämpliga. Dessa tekniker förstås bäst som metoder för att hitta en nivåuppsättningsbeskrivning av den underliggande bitvis konstanta signalen.
Stegdetektering som 0-graders splinepassning
Många algoritmer anpassar explicit 0-graders splines till den brusiga signalen för att detektera steg (inklusive stegvisa hoppplaceringsmetoder), men det finns andra populära algoritmer som också kan ses vara splineanpassningsmetoder efter viss transformation, till exempel total variationsnedsättning .
Generaliserad stegdetektering genom styckvis konstant nedtoning
Alla ovan nämnda algoritmer har vissa fördelar och nackdelar under speciella omständigheter, men ändå är ett förvånansvärt stort antal av dessa stegdetekteringsalgoritmer specialfall av en mer allmän algoritm. Denna algoritm innebär minimering av en global funktion:
-
()
Här är xi för i = 1, ...., N är den tidsdiskreta insignalen med längden N och mi är utsignalen från algoritmen. Målet är att minimera H [ m ] med avseende på utsignalen m . Formen av funktionen bestämmer den specifika algoritmen. Välj till exempel:
där I ( S ) = 0 om villkoret S är falskt, och en annars, erhåller den totala variationsavblödningsalgoritmen med regulariseringsparameter . Liknande:
leder till medelförskjutningsalgoritmen , när man använder en Euler-integrator med adaptiv stegstorlek initierad med insignalen x . Här W > 0 en parameter som bestämmer stödet för medelskiftkärnan. Ett annat exempel är:
leder till det bilaterala filtret , där är den tonala kärnparametern och W är det rumsliga kärnstödet. Ytterligare ett specialfall är:
specificerar en grupp algoritmer som girigt försöker passa 0-graders splines till signalen. Här, definieras som noll om x = 0, och en annars.
Många av funktionalerna i ekvation ( 1 ) som definieras av det särskilda valet av är konvexa : de kan minimeras med metoder från konvex optimering . Ytterligare andra är icke-konvexa men en rad algoritmer för att minimera dessa funktioner har utarbetats.
Stegdetektering med hjälp av Potts-modellen
En klassisk variationsmetod för stegdetektering är Potts-modellen. Det ges av det icke-konvexa optimeringsproblemet
Termen straffar antalet hopp och termen datatrohet x . Parametern γ > 0 styr avvägningen mellan regularitet och datatillförlitlighet . Eftersom minimizern är styckvis konstant ges stegen av placeringarna som inte är noll för gradienten . För och finns det snabba algoritmer som ger en exakt lösning på Potts-problemet i .
![H[m]=\sum_{i=1}^N\sum_{j=1}^N \Lambda(x_i-m_j,m_i-m_j,x_i-x_j,i-j)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f718c1c4d65b77e0644808d9b1addc736151699f)















