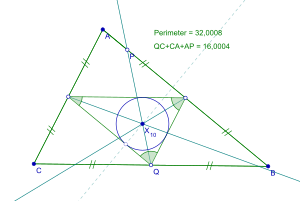
Spieker cirkel
Inom geometri är incirkeln av den mediala triangeln i en triangel Spieker-cirkeln , uppkallad efter 1800-talets tyska geometer Theodor Spieker . Dess centrum, Spieker-centrumet , är förutom att vara mitten av den mediala triangeln, massacentrum för triangelns likformiga täthet. Spiekers centrum är också den punkt där alla tre klyvarna i triangeln (omkretshalvledar med en ändpunkt vid en sidas mittpunkt) skär varandra.
Historia
Spieker-cirkeln och Spieker-centret är uppkallade efter Theodor Spieker , en matematiker och professor från Potsdam , Tyskland. [ citat behövs ] År 1862 publicerade han Lehrbuch der ebenen geometrie mit übungsaufgaben für höhere lehranstalten , som handlade om plan geometri. [ citat behövs ] På grund av denna publikation, inflytelserik i många berömda vetenskapsmäns och matematikers liv, inklusive Albert Einstein , blev Spieker den matematiker som Spieker-cirkeln och centrumet namngavs efter.
Konstruktion
För att hitta Spieker-cirkeln för en triangel måste den mediala triangeln först konstrueras från mittpunkterna på varje sida av den ursprungliga triangeln. Cirkeln är sedan konstruerad på ett sådant sätt att varje sida av den mediala triangeln tangerar cirkeln inom den mediala triangeln, vilket skapar incirkeln . Detta cirkelcentrum kallas Spiekercentrum .
Nagel pekar och linjer
Spieker cirklar har också relationer till Nagel poäng . Triangelns centrum och Nagelpunkten bildar en linje inom Spieker-cirkeln. Mitten av detta linjesegment är Spiekers centrum. Nagellinjen bildas av triangelns centrum, Nagelpunkten och triangelns tyngdpunkt . Spiekers centrum kommer alltid att ligga på denna linje.
Niopunktscirkel och Eulerlinje
Spieker-cirklar visade sig först vara mycket lika niopunktscirklar av Julian Coolidge. Vid denna tidpunkt identifierades den ännu inte som Spieker-cirkeln, men den kallas för "P-cirkeln" genom hela boken. Niopunktscirkeln med Euler-linjen och Spieker-cirkeln med Nagel-linjen är analoga med varandra, men är inte dualer , utan har bara dubbelliknande likheter. En likhet mellan niopunktscirkeln och Spiekercirkeln handlar om deras konstruktion. Den niopunktscirkeln är den omskrivna cirkeln i den mediala triangeln, medan Spieker-cirkeln är den inskrivna cirkeln i den mediala triangeln. Med relation till deras tillhörande linjer, hänför sig incenter för Nagel-linjen till circumcenter för Euler-linjen. En annan analog punkt är Nagel-punkten och otocentret , med Nagel-punkten associerad med Spieker-cirkeln och ortocentrum associerad med niopunktscirkeln. Varje cirkel möter sidorna av den mediala triangeln där linjerna från ortocentret, eller Nagel-punkten, till toppen av den ursprungliga triangeln möter sidorna av den mediala triangeln.
Spieker konisk
Niopunktscirkeln med Eulerlinjen generaliserades till den niopunktskoniska. Genom en liknande process, på grund av de analoga egenskaperna hos de två cirklarna, kunde Spieker-cirkeln också generaliseras till Spieker-koniska. Spieker-koniken finns fortfarande inom den mediala triangeln och berör varje sida av den mediala triangeln, men den möter inte de sidorna av triangeln på samma punkter. Om linjer konstrueras från varje vertex av den mediala triangeln till Nagel-punkten, kan mittpunkten för var och en av dessa linjer hittas. Dessutom hittas mittpunkterna på varje sida av den mediala triangeln och kopplas till mittpunkten på den motsatta linjen genom Nagelpunkten. Var och en av dessa linjer delar en gemensam mittpunkt, S. Med var och en av dessa linjer reflekterad genom S, blir resultatet 6 punkter inom den mediala triangeln. Rita en kägel genom valfri 5 av dessa reflekterade punkter och könen kommer att röra vid den sista punkten. Detta bevisades av de Villiers 2006.
Spiekers radikala krets
Spieker- radikalcirkeln är cirkeln, centrerad vid Spiekers centrum, som är ortogonal mot den mediala triangelns tre excirklar .
- Johnson, Roger A. (1929). Modern geometri . Boston: Houghton Mifflin. Dover nytryck, 1960.
- Kimberling, Clark (1998). "Triangelcentrum och centrala trianglar". Congressus Numerantium . 129 : i–xxv, 1–295.
externa länkar
- Spieker Conic och generalisering av Nagel-linjen vid Dynamic Geometry Sketches Generaliserar Spieker-cirkeln och tillhörande Nagel-linje.