Salinon

Salinon (röd) och cirkeln (blå) har samma area.

Salinon (som betyder "saltkällare" på grekiska) är en geometrisk figur som består av fyra halvcirklar . Det introducerades först i Lemmas bok , ett verk som tillskrivs Arkimedes .

Konstruktion

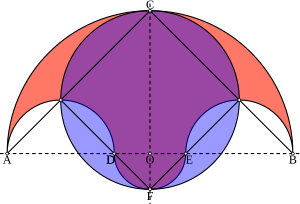
Låt A , D , E och B vara fyra punkter på en linje i planet, i den ordningen, med AD = EB . Låt O vara bisektrisen av segment AB (och av DE ). Rita halvcirklar ovanför linjen AB med diametrarna AB , AD och EB , och en annan halvcirkel nedanför med diameter DE . En salinon är figuren som avgränsas av dessa fyra halvcirklar.

Egenskaper

Område

Arkimedes introducerade salinon i sin Lemmas bok genom att tillämpa bok II, proposition 10 av Euklids element . Arkimedes noterade att "ytan av figuren som begränsas av omkretsen av alla halvcirklar [är] lika med arean av cirkeln på CF som diameter."

Nämligen, om $r_{1}$ är radien för en stor omslutande halvcirkel och $r_{2}$ är radien för den lilla centrala halvcirkeln, då är salinonens area:

$$A={\frac {1}{4}}\pi \left(r_{1}+r_{2}\right)^{2}.$$

Arbelos

Skulle punkterna D och E konvergera med O , skulle det bilda en arbelos , en annan av Arkimedes skapelser, med symmetri längs y -axeln .

Se även

• Lune av Hippokrates

externa länkar

• L'arbelos. Partie II av Hamza Khelif på www.images.math.cnrs.fr av CNRS