Statisk enuppgiftsblankett

I kompilatordesign är statisk enkeltilldelningsform ( ofta förkortad som SSA-form eller helt enkelt SSA ) en egenskap hos en mellanrepresentation (IR) som kräver att varje variabel tilldelas exakt en gång och definieras innan den används. Befintliga variabler i den ursprungliga IR är uppdelade i versioner , nya variabler typiskt indikerade av det ursprungliga namnet med en nedskrivning i läroböcker, så att varje definition får sin egen version. I SSA-form use-def-kedjor explicita och var och en innehåller ett enda element.

SSA föreslogs av Barry K. Rosen, Mark N. Wegman och F. Kenneth Zadeck 1988. Ron Cytron, Jeanne Ferrante och de tidigare tre forskarna vid IBM utvecklade en algoritm som kan beräkna SSA-formen effektivt.

Man kan förvänta sig att hitta SSA i en kompilator för Fortran , C , C++ eller Java (Android Runtime); I funktionella språkkompilatorer , såsom de för Scheme och ML , används vanligen fortsättningsövergångsstil (CPS). SSA motsvarar formellt en väluppfostrad delmängd av CPS exklusive icke-lokalt kontrollflöde, vilket inte inträffar när CPS används som mellanliggande representation. Så optimeringar och transformationer formulerade i termer av det ena gäller omedelbart det andra.

Fördelar

Den primära användbarheten av SSA kommer från hur den samtidigt förenklar och förbättrar resultaten av en mängd olika kompilatoroptimeringar genom att förenkla egenskaperna hos variabler. Tänk till exempel på denna kodbit:

y := 1 y := 2 x := y

Människor kan se att den första uppgiften inte är nödvändig, och att värdet av y som används i den tredje raden kommer från den andra tilldelningen av y . Ett program skulle behöva utföra nå definitionsanalys för att fastställa detta. Men om programmet är i SSA-form är båda dessa omedelbara:

 y  1  := 1 y  2  := 2 x  1  := y  2 

för kompilatoroptimering som antingen är aktiverade eller kraftigt förbättrade genom användningen av SSA inkluderar:

• Konstant utbredning – omvandling av beräkningar från körtid till kompileringstid, t.ex. behandla instruktionen a=3*4+5; som om det vore a=17;
• Utbredning av värdeintervall – förberäkna de potentiella intervallen som en beräkning kan vara, vilket gör det möjligt att skapa grenförutsägelser i förväg
• Gles villkorlig konstant utbredning – avståndskontrollera några värden, vilket gör att tester kan förutsäga den mest sannolika grenen
• Eliminering av död kod – ta bort kod som inte har någon effekt på resultaten
• Global värdenumrering – ersätt dubbla beräkningar som ger samma resultat
• Eliminering av partiell redundans – tar bort dubbletter av beräkningar som tidigare utförts i vissa grenar av programmet
• Styrkeminskning – ersätt dyra operationer med billigare men likvärdiga, t.ex. ersätt heltalsmultiplicera eller dividera med 2 potenser med det potentiellt billigare skift åt vänster (för multiplicera) eller skift åt höger (för divide).
• Registerallokering – optimera hur det begränsade antalet maskinregister får användas för beräkningar

Konverterar till SSA

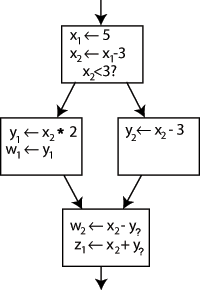
Att konvertera vanlig kod till SSA-form är i första hand en fråga om att ersätta målet för varje tilldelning med en ny variabel, och att ersätta varje användning av en variabel med den "version" av variabeln som når den punkten . Tänk till exempel på följande kontrollflödesdiagram :

Att ändra namnet på vänster sida av "x $\leftarrow$ x - 3" och ändra följande användningar av x till det nya namnet skulle lämna programmet oförändrat. Detta kan utnyttjas i SSA genom att skapa två nya variabler: x ₁ och x ₂ , som var och en endast tilldelas en gång. På samma sätt ger särskiljande sänkningar till alla andra variabler:

Det är tydligt vilken definition varje användning hänvisar till, förutom ett fall: båda användningarna av y i det nedre blocket kan hänvisa till antingen y ₁ eller y ₂ , beroende på vilken väg kontrollflödet tog.

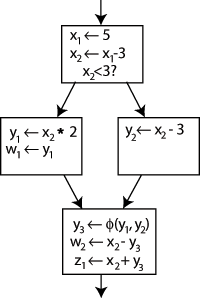
För att lösa detta infogas en speciell sats i det sista blocket, som kallas en Φ (Phi) funktion . Detta uttalande kommer att generera en ny definition av y som kallas y ₃ genom att "välja" antingen y ₁ eller y ₂ , beroende på kontrollflödet i det förflutna.

Nu kan det sista blocket helt enkelt använda y ₃ , och det korrekta värdet kommer att erhållas åt båda hållen. En Φ-funktion för x behövs inte: endast en version av x , nämligen x ₂ , når denna plats, så det är inga problem (med andra ord, Φ( x ₂ , x ₂ )= x ₂ ).

Givet ett godtyckligt kontrollflödesdiagram kan det vara svårt att säga var man ska infoga Φ-funktioner och för vilka variabler. Denna allmänna fråga har en effektiv lösning som kan beräknas med hjälp av ett koncept som kallas dominansgränser (se nedan).

Φ funktioner är inte implementerade som maskinoperationer på de flesta maskiner. En kompilator kan implementera en Φ-funktion genom att infoga "flytta"-operationer i slutet av varje föregångare. I exemplet ovan kan kompilatorn infoga ett drag från y ₁ till y ₃ i slutet av mitten-vänster-blocket och ett drag från y ₂ till y ₃ i slutet av mitt-höger-blocket. Dessa flyttoperationer kanske inte hamnar i den slutliga koden baserat på kompilatorns registertilldelningsprocedur . Men det här tillvägagångssättet kanske inte fungerar när samtidiga operationer spekulativt producerar indata till en Φ-funktion, vilket kan hända på maskiner med omfattande problem . Vanligtvis har en bredutgåvad maskin en valinstruktion som används i sådana situationer av kompilatorn för att implementera Φ-funktionen.

Enligt Kenny Zadeck var Φ-funktioner ursprungligen kända som falska funktioner medan SSA utvecklades på IBM Research på 1980-talet. Det formella namnet på en Φ-funktion antogs först när verket först publicerades i en akademisk uppsats.

Beräknar minimal SSA med hjälp av dominansgränser

I ett kontrollflödesdiagram sägs en nod A strikt dominera en annan nod B om det är omöjligt att nå B utan att passera genom A först. Med andra ord, om nod B nås, kan det antas att A har körts. A sägs dominera B (eller B domineras av A) om antingen A strikt dominerar B eller A = B.

En nod som överför kontrollen till en nod A kallas en omedelbar föregångare till A.

Dominansgränsen för nod A är uppsättningen av noder B där A inte strikt dominerar B, utan dominerar någon omedelbar föregångare till B. Det här är de punkter där flera styrvägar smälter samman igen till en enda väg .

Till exempel i följande kod:

[1] x = random() om x < 0,5 [2] resultat = "huvuden" annars [3] resultat = "svansar" slut [4] print(resultat)

nod 1 dominerar strikt 2, 3 och 4, och den omedelbara föregångaren till nod 4 är noderna 2 och 3.

Dominansgränser definierar de punkter där Φ-funktioner behövs. I exemplet ovan, när kontroll skickas till nod 4, beror definitionen av det använda resultatet på om kontroll skickades från nod 2 eller 3. Φ funktioner behövs inte för variabler som definieras i en dominator, eftersom det bara finns en möjlig definition som kan ansöka.

Det finns en effektiv algoritm för att hitta dominansgränser för varje nod. Denna algoritm beskrevs ursprungligen i "Efficiently Computing Static Single Assignment Form and the Control Graph" av Ron Cytron, Jeanne Ferrante, et al 1991.

Keith D. Cooper, Timothy J. Harvey och Ken Kennedy från Rice University beskriver en algoritm i sin artikel med titeln A Simple, Fast Dominance Algorithm :

 för varje  nod b dominance_frontier(b) := {}  för varje  nod b  om  antalet omedelbara föregångare för b ≥ 2  för varje  p  i  omedelbara föregångare till b löpare := p  medan  löpare ≠ idom(b) dominance_frontier(runner): = dominance_frontier(runner) ∪ { b } runner := idom(runner) 

I koden ovan är idom(b) den omedelbara dominatorn för b, den unika noden som strikt dominerar b men inte strikt dominerar någon annan nod som strikt dominerar b.

Variationer som minskar antalet Φ-funktioner

"Minimal" SSA infogar det minimala antalet Φ-funktioner som krävs för att säkerställa att varje namn tilldelas ett värde exakt en gång och att varje referens (användning) av ett namn i det ursprungliga programmet fortfarande kan referera till ett unikt namn. (Det senare kravet behövs för att säkerställa att kompilatorn kan skriva ner ett namn för varje operand i varje operation.)

Vissa av dessa Φ-funktioner kan dock vara döda . Av denna anledning producerar minimal SSA inte nödvändigtvis det minsta Φ-funktionerna som behövs för en specifik procedur. För vissa typer av analys är dessa Φ-funktioner överflödiga och kan göra att analysen går mindre effektivt.

Beskärs SSA

Beskuren SSA-form bygger på en enkel observation: Φ-funktioner behövs endast för variabler som är "live" efter Φ-funktionen. (Här betyder "live" att värdet används längs någon väg som börjar vid Φ-funktionen i fråga.) Om en variabel inte är live, kan resultatet av Φ-funktionen inte användas och tilldelningen av Φ-funktionen är död .

Konstruktion av beskuren SSA-form använder live-variabel information i Φ-funktionsinsättningsfasen för att avgöra om en given Φ-funktion behövs. Om det ursprungliga variabelnamnet inte är aktivt vid Φ-funktionens insättningspunkt, infogas inte Φ-funktionen.

En annan möjlighet är att behandla beskärning som ett problem med eliminering av döda koder . Då är en Φ-funktion live endast om någon användning i inmatningsprogrammet kommer att skrivas om till den, eller om den kommer att användas som ett argument i en annan Φ-funktion. När du anger SSA-formuläret skrivs varje användning om till närmaste definition som dominerar den. En Φ-funktion kommer då att betraktas som live så länge det är den närmaste definitionen som dominerar minst en användning, eller minst ett argument för en live Φ.

Halvbeskärad SSA

Halvbeskärad SSA-form är ett försök att minska antalet Φ-funktioner utan att ådra sig den relativt höga kostnaden för att beräkna live-variabel information. Den är baserad på följande observation: om en variabel aldrig är aktiv vid inträde i ett basblock behöver den aldrig en Φ-funktion. Under SSA-konstruktion utelämnas Φ-funktioner för alla "blocklokala" variabler.

Att beräkna uppsättningen av blocklokala variabler är en enklare och snabbare procedur än fullständig analys av levande variabel, vilket gör semi-beskärad SSA-form mer effektiv att beräkna än beskuren SSA-form. Å andra sidan kommer halvbeskärad SSA-form att innehålla fler Φ-funktioner.

Blockera argument

Blockargument är ett alternativ till Φ-funktioner som är representativt identiska men som i praktiken kan vara mer bekväma under optimering. Blocken namnges och tar en lista med blockargument, noterade som funktionsparametrar. När ett block anropas är blockargumenten bundna till specificerade värden. Swift och LLVM:s mellanrepresentation på flera nivåer använder blockargument.

Konverterar från SSA-formulär

SSA-formulär används normalt inte för direkt exekvering (även om det är möjligt att tolka SSA), och det används ofta "ovanpå" en annan IR som den förblir i direkt korrespondens med. Detta kan åstadkommas genom att "konstruera" SSA som en uppsättning funktioner som mappar mellan delar av den befintliga IR (grundläggande block, instruktioner, operander, etc. ) och dess SSA-motsvarighet. När SSA-formuläret inte längre behövs kan dessa mappningsfunktioner kasseras, vilket bara lämnar den nu optimerade IR.

Att utföra optimeringar på SSA-formulär leder vanligtvis till intrasslade SSA-webb, vilket innebär att det finns Φ instruktioner vars operander inte alla har samma rotoperand. I sådana fall används färg-ut- algoritmer för att komma ut ur SSA. Naiva algoritmer introducerar en kopia längs varje föregångare som gjorde att en källa med annan rotsymbol placerades i Φ än destinationen för Φ. Det finns flera algoritmer för att komma ut ur SSA med färre kopior, de flesta använder interferensgrafer eller någon approximation av det för att göra kopia coalescing.

Tillägg

Tillägg till SSA-formulär kan delas in i två kategorier.

Byte av schematillägg ändrar bytekriteriet. Kom ihåg att SSA-formuläret byter namn på varje variabel när den tilldelas ett värde. Alternativa scheman inkluderar statisk engångsform (som byter namn på varje variabel vid varje sats när den används) och statisk enkel informationsform (som byter namn på varje variabel när den tilldelas ett värde, och vid post-dominansgränsen).

Funktionsspecifika tillägg behåller den enskilda tilldelningsegenskapen för variabler, men införlivar ny semantik för att modellera ytterligare funktioner. Vissa funktionsspecifika tillägg modellerar programmeringsspråksfunktioner på hög nivå som arrayer, objekt och aliaspekare. Andra funktionsspecifika tillägg modellerar arkitektoniska funktioner på låg nivå som spekulationer och förutsägelser.

Kompilatorer som använder SSA-formulär

SSA-form är en relativt ny utveckling inom kompilatorgemenskapen. Som sådan använder många äldre kompilatorer endast SSA-formen för någon del av kompileringen eller optimeringsprocessen, men de flesta förlitar sig inte på det. Exempel på kompilatorer som är mycket beroende av SSA-formulär inkluderar:

• ETH Oberon-2- kompilatorn var ett av de första offentliga projekten som införlivade "GSA", en variant av SSA.
• LLVM Compiler Infrastructure använder SSA-formulär för alla skalära registervärden (allt utom minne) i sin primära kodrepresentation . SSA-formuläret elimineras först när registertilldelning sker, sent i kompileringsprocessen (ofta vid länktid).
• Open64 - kompilatorn använder SSA-form i sin globala skalära optimerare, även om koden förs till SSA-form före och tas ut ur SSA-form efteråt. Open64 använder tillägg till SSA-form för att representera minne i SSA-form såväl som skalära värden.
• använder GCC, GNU Compiler Collection , i stor utsträckning SSA. Gränssnitten genererar " GENERIC "-kod som sedan konverteras till " GIMPLE " -kod av "gimplifier". Högnivåoptimeringar tillämpas sedan på SSA-formen "GIMPLE". Den resulterande optimerade mellankoden översätts sedan till RTL , på vilken lågnivåoptimeringar tillämpas. De arkitekturspecifika backends förvandlar slutligen RTL till assemblerspråk .
• IBM: s adaptiva Java virtuella maskin med öppen källkod , Jikes RVM , använder utökad Array SSA, en förlängning av SSA som tillåter analys av skalärer, arrayer och objektfält i ett enhetligt ramverk. Extended Array SSA-analys är endast aktiverad på den maximala optimeringsnivån, som tillämpas på de vanligaste delarna av koden.
• År 2002 modifierade forskare IBM:s JikesRVM (som hette Jalapeño vid den tiden) för att köra både standard Java- bytecode och en typsäker SSA ( SafeTSA ) bytecode-klassfiler, och visade betydande prestandafördelar med att använda SSA-bytecode.
• Oracles HotSpot Java Virtual Machine använder ett SSA-baserat mellanspråk i sin JIT-kompilator .
• Microsoft Visual C++ kompilatorbackend tillgänglig i Microsoft Visual Studio 2015 Update 3 använder SSA
• Mono använder SSA i sin JIT-kompilator som heter Mini.
• jackcc är en kompilator med öppen källkod för den akademiska instruktionsuppsättningen Jackal 3.0. Den använder en enkel 3-operandkod med SSA för sin mellanliggande representation. Som en intressant variant ersätter den Φ-funktioner med en så kallad SAME-instruktion, som instruerar registerfördelaren att placera de två live-intervallen i samma fysiska register.
• Även om den inte är en kompilator, använder Boomerang- dekompilatorn SSA-form i sin interna representation. SSA används för att förenkla uttryckspridning, identifiera parametrar och avkastning, bevarandeanalys och mer.
• Portable.NET använder SSA i sin JIT-kompilator.
• libFirm en helt grafbaserad SSA-mellanrepresentation för kompilatorer. libFirm använder SSA-formulär för alla skalära registervärden fram till kodgenerering med hjälp av en SSA-medveten registerallokator.
• Illinois Concert Compiler ca 1994 använde en variant av SSA som kallas SSU (Static Single Use) som byter namn på varje variabel när den tilldelas ett värde, och i varje villkorligt sammanhang där den variabeln används; huvudsakligen det statiska enda informationsformuläret som nämns ovan. SSU-formuläret finns dokumenterat i John Plevyaks doktorsavhandling .
• COINS-kompilatorn använder SSA-formuläroptimeringar som förklaras här .
• Mozilla Firefox SpiderMonkey JavaScript-motor använder SSA-baserad IR .
• Chromium V8 JavaScript-motorn implementerar SSA i sin vevaxelkompilatorinfrastruktur som tillkännagavs i december 2010
• PyPy använder en linjär SSA-representation för spår i sin JIT-kompilator.
• Androids virtuella dator Dalvik använder SSA i sin JIT-kompilator .
• Androids nya optimeringskompilator för Android Runtime använder SSA för sin IR.
• Standard ML-kompilatorn MLton använder SSA på ett av dess mellanspråk.
• LuaJIT använder sig mycket av SSA-baserade optimeringar.
• PHP- och hackkompilatorn HHVM använder SSA i sin IR .
• Reservoir Labs R-Stream-kompilator stöder icke-SSA (quad list), SSA och SSI (Static Single Information)-formulär.
• Go (1.7: endast för x86-64-arkitektur; 1.8: för alla arkitekturer som stöds).
• SPIR-V , skuggspråksstandarden för Vulkans grafik-API och kärnspråket för OpenCL Compute API, är en SSA-representation.
• Olika Mesa- drivrutiner via NIR, en SSA-representation för skuggspråk.
• WebKit använder SSA i sina JIT-kompilatorer.
• Swift definierar sin egen SSA-form ovanför LLVM IR, kallad SIL (Swift Intermediate Language).
• Erlang skrev om sin kompilator i OTP 22.0 för att "internt använda en mellanrepresentation baserad på Static Single Assignment (SSA)." Med planer för ytterligare optimeringar byggda ovanpå SSA i framtida utgåvor.

Allmänna referenser

•      Appel, Andrew W. (1999). Modern kompilatorimplementering i ML . Cambridge University Press. ISBN 978-0-521-58274-2 . Finns även i Java ( ISBN 0-521-82060-X , 2002) och C ( ISBN 0-521-60765-5 , 1998) versioner.
•   Cooper, Keith D. & Torczon, Linda (2003). Konstruera en kompilator . Morgan Kaufmann. ISBN 978-1-55860-698-2 .
•   Muchnick, Steven S. (1997). Avancerad kompilatordesign och implementering . Morgan Kaufmann. ISBN 978-1-55860-320-2 .
• Kelsey, Richard A. (mars 1995). "En överensstämmelse mellan fortsättningspasseringsstil och statisk singeluppgiftsform" . ACM SIGPLAN-meddelanden . 30 (3): 13–22. doi : 10.1145/202530.202532 .
•   Appel, Andrew W. (april 1998). "SSA är funktionell programmering". ACM SIGPLAN-meddelanden . 33 (4): 17–20. doi : 10.1145/278283.278285 . S2CID 207227209 .
• Pop, Sebastian (2006). "SSA Representation Framework: Semantics, Analyzes and GCC Implementation" (PDF) . {{ citera journal }} : Citera journal kräver |journal= ( hjälp )
•   Matthias Braun; Sebastian Buchwald; Sebastian Hack; Roland Leißa; Christoph Mallon; Andreas Zwinkau (2013), "Simple and Efficient Construction of Static Single Assignment Form" , Compiler Construction , Lecture Notes in Computer Science, vol. 7791, Springer Berlin Heidelberg, s. 102–122, doi : 10.1007/978-3-642-37051-9_6 , ISBN 978-3-642-37050-2 , hämtad 24 mars 2013

externa länkar

• Bosscher, Steven; och Novillo, Diego. GCC får ett nytt Optimizer Framework . En artikel om GCC:s användning av SSA och hur det förbättras jämfört med äldre IR:er.
• SSA-bibliografin . Omfattande katalog med SSA-forskningsartiklar.
• Zadeck, F. Kenneth. "The Development of Static Single Assignment Form" , december 2007 tal om ursprunget till SSA.
• VV.AA. "SSA-baserad kompilatordesign" (2014)