Rosenbrock funktion

Plott av Rosenbrock-funktionen av två variabler. Här är $a=1,b=100$ , och minimivärdet på noll är vid $(1,1)$ .

Inom matematisk optimering är Rosenbrock-funktionen en icke- konvex funktion , introducerad av Howard H. Rosenbrock 1960, som används som ett prestationstestproblem för optimeringsalgoritmer . Det är också känt som Rosenbrocks dal eller Rosenbrocks bananfunktion .

Det globala minimumet är inuti en lång, smal, parabolformad platt dal. Att hitta dalen är trivialt. Att konvergera till det globala minimumet är dock svårt.

Funktionen definieras av

$f(x,y)=(ax)^{2}+b(yx^{2})^{ 2}$

Den har ett globalt minimum vid $(x,y)=(a,a^{2})$ , där $f (x,y)=0$ . Vanligtvis är dessa parametrar inställda så att $a=1$ och $b=100$ . Endast i det triviala fallet där $a=0$ är funktionen symmetrisk och minimum är vid origo.

Multidimensionella generaliseringar

Två varianter är vanliga.

Animation av Rosenbrocks funktion av tre variabler.

Det ena är summan av $N/2$ okopplade 2D Rosenbrock-problem, och definieras endast för även $N$ :

$f(\mathbf {x} )=f(x_{1},x_{2},\dots ,x_{N})=\summa _{i=1}^{N/2}\left[ 100(x_{2i-1}^{2}-x_{2i})^{2}+(x_{2i-1}-1)^{2}\höger].$

Denna variant har förutsägbart enkla lösningar.

En andra, mer involverad variant är

$f(\mathbf {x} )=\sum _{i=1}^{N-1}[100(x_{i+1}-x_{i}^{2})^{2}+ (1-x_{i})^{2}]\quad {\mbox{där}}\quad \mathbf {x} =(x_{1},\ldots ,x_{N})\i \mathbb {R } ^{N}.$

har exakt ett minimum för $N=3$ (at $(1,1,1)$ ) och exakt två minima för $4 \leq N\leq 7$ —det globala minimum vid $(1,1,...,1)$ och ett lokalt minimum nära ${\hat {\mathbf {x} }}=(-1,1,\dots ,1)$ . Detta resultat erhålls genom att sätta gradienten för funktionen lika med noll, och notera att den resulterande ekvationen är en rationell funktion av $x$ . För litet $N$ kan polynomen bestämmas exakt och Sturms sats kan användas för att bestämma antalet reella rötter, medan rötterna kan avgränsas i området $|x_{i}|<2.4$ . För större $N$ bryts denna metod ner på grund av storleken på de inblandade koefficienterna.

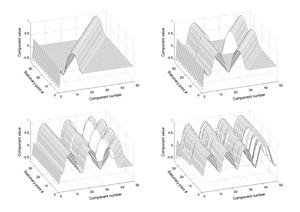
Stationära punkter

Många av de stationära punkterna i funktionen uppvisar ett regelbundet mönster när de plottas. Denna struktur kan utnyttjas för att lokalisera dem.

Rosenbrockrötter som uppvisar puckelstrukturer

Optimeringsexempel

Nelder-Mead-metoden tillämpas på Rosenbrock-funktionen

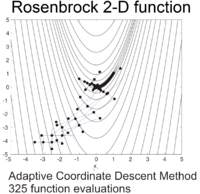
Rosenbrock-funktionen kan optimeras effektivt genom att anpassa lämpligt koordinatsystem utan att använda någon gradientinformation och utan att bygga lokala approximationsmodeller (i motsats till många derivatfria optimerare). Följande figur illustrerar ett exempel på 2-dimensionell Rosenbrock-funktionsoptimering genom adaptiv koordinatnedstigning från startpunkten $x_{0}=(-3,-4)$ . Lösningen med funktionsvärdet $10^{-10}$ kan hittas efter 325 funktionsutvärderingar.

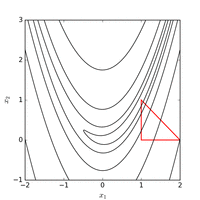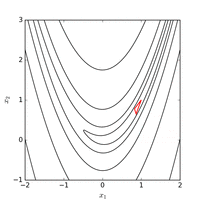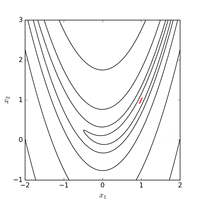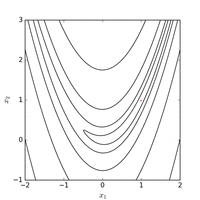
Med Nelder–Mead-metoden från startpunkten $x_{0}=(-1,1)$ med en vanlig initial simplex hittas ett minimum med funktionsvärdet ${ \displaystyle 1.36\cdot 10^{-10}}$ efter 185 funktionsutvärderingar. Figuren nedan visualiserar utvecklingen av algoritmen.

Se även

• Testa funktioner för optimering

externa länkar

• Rosenbrock funktionsdiagram i 3D
• Weisstein, Eric W. "Rosenbrock Function" . MathWorld .