Rising sun lemma
I matematisk analys är det uppgående solens lemma ett lemma som beror på Frigyes Riesz , som används i beviset för Hardy–Littlewoods maximala teorem . Lemmat var en föregångare i en dimension av Calderón-Zygmund-lemmat .
Lemmat heter så här:
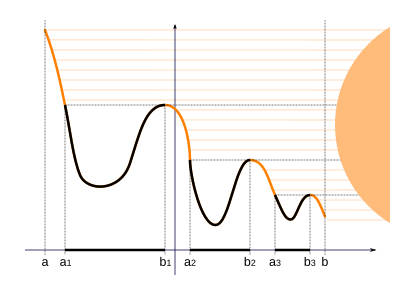
- Antag att g är en reellt värderad kontinuerlig funktion på intervallet [ a , b ] och S är mängden x i [ a , b ] så att det finns en y ∈( x , b ] med g ( y ) > g ( x ). (Observera att b inte kan vara i S , även om a kan vara det.) Definiera E = S ∩ ( a , b ).
- Då är E en öppen mängd, och den kan skrivas som en räkningsbar union av disjunkta intervall
- så att g ( a k ) = g ( b k ), om inte a k = a ∈ S för något k , i vilket fall g ( a ) < g ( b k ) för det ena k . Dessutom, om x ∈ ( a k , b k ), så g ( x ) < g ( b k ).
Det färgglada namnet på lemma kommer från att föreställa sig grafen för funktionen g som ett bergslandskap, med solen som skiner horisontellt från höger. Uppsättningen E består av punkter som ligger i skuggan.
Bevis
Vi behöver ett lemma: Antag att [ c , d ) ⊂ S , men d ∉ S . Sedan g ( c ) < g ( d ). För att bevisa detta, antag att g ( c ) ≥ g ( d ). Sedan g sitt maximum på [ c , d ] vid någon punkt z < d . Eftersom z ∈ S finns ett y i ( z , b ] med g ( z ) < g ( y ). Om y ≤ d , så skulle g inte nå sitt maximum på [ c , d ] vid z . Således, y ∈ ( d , b ], och g ( d ) ≤ g ( z ) < g ( y ) Detta betyder att d ∈ S , vilket är en motsägelse, och därmed etablerar lemma.
Mängden E är öppen, så den är sammansatt av en räknebar förening av disjunkta intervall ( a k , b k ).
Det följer omedelbart av lemmat att g ( x ) < g ( b k ) för x in ( a k , b k ). Eftersom g är kontinuerlig måste vi också ha g ( a k ) ≤ g ( b k ).
Om a k ≠ a eller a ∉ S , så a k ∉ S , alltså g ( a k ) ≥ g ( b k ), för annars a k ∈ S . Således är g ( a k ) = g ( b k ) i dessa fall.
Slutligen, om a k = a ∈ S , säger lemmat oss att g ( a ) < g ( b k ).
Anteckningar
- Duren, Peter L. (2000), Theory of H p Spaces , New York: Dover Publications, ISBN 0-486-41184-2
- Garling, DJH (2007), Inequalities: a journey into linear analysis , Cambridge University Press, ISBN 978-0-521-69973-0
- Korenovskyy, AA; AK Lerner; AM Stokolos (november 2004), "On a multidimensional form of F. Riesz's "rising sun" lemma", Proceedings of the American Mathematical Society , 133 ( 5): 1437–1440, doi : 10.1090/S0002-9939-534-07 -1
- Riesz, Frédéric (1932), "Sur un Théorème de Maximum de Mm. Hardy et Littlewood" , Journal of the London Mathematical Society , 7 (1): 10–13, doi : 10.1112/jlms/s1-7.1.10 , arkiverad från originalet 2013-04-15 , hämtat 2008-07-21
- Stein, Elias (1998), "Singular integrals: The Roles of Calderón and Zygmund" (PDF) , Notices of the American Mathematical Society , 45 (9): 1130–1140 .
- Tao, Terence (2011), An Introduction to Measure Theory , Graduate Studies in Mathematics , vol. 126, American Mathematical Society, ISBN 978-0821869192
- Zygmund, Antoni (1977), Trigonometric Series. Vol. I, II (andra upplagan), Cambridge University Press, ISBN 0-521-07477-0