Regression-kriging

I tillämpad statistik och geostatistik är regression-kriging ( RK ) en rumslig prediktionsteknik som kombinerar en regression av den beroende variabeln på hjälpvariabler (som parametrar härledda från digital höjdmodellering, fjärranalys/bilder och tematiska kartor) med interpolation ( kriging ) av regressionsresterna. Det är matematiskt ekvivalent med interpolationsmetoden som omväxlande kallas universell kriging och kriging med extern drift, där hjälpprediktorer används direkt för att lösa krigingvikterna.

BLUP för rumslig data

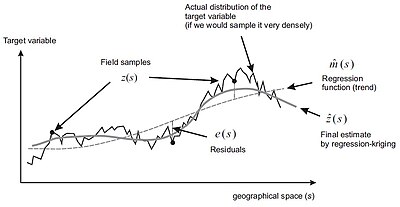
Den universella modellen för rumslig variationsschema.

Regression-kriging är en implementering av den bästa linjära opartiska prediktorn (BLUP) för rumslig data, dvs den bästa linjära interpolatorn som antar den universella modellen för rumslig variation. Matheron (1969) föreslog att ett värde för en målvariabel på någon plats kan modelleras som en summa av de deterministiska och stokastiska komponenterna:

Z(\mathbf {s} )=m(\mathbf {s} )+\varepsilon '(\mathbf {s} )+ \varepsilon ''

som han kallade universell modell för rumslig variation . Både deterministiska och stokastiska komponenter av rumslig variation kan modelleras separat. Genom att kombinera de två metoderna får vi:

{\ hat {z}}(\mathbf {s} _{0})={\hat {m}}(\mathbf {s} _{0})+{\hat {e}}(\mathbf {s} _ {0})=\summa \limits _{k=0}^{p}{{\hat {\beta}}_{k}\cdot q_{k}(\mathbf {s} _{0})} +\sum \limits _{i=1}^{n}\lambda _{i}\cdot e(\mathbf {s} _{i})

där ${\hat {m}}(\mathbf {s} _{0})$ är den anpassade deterministiska delen, ${\hat {e}}( \mathbf {s} _{0})$ är den interpolerade residualen, ${\hat {\beta }}_{k}$ är uppskattade deterministiska modellkoefficienter ( ${\hat { \beta }}_{0}$ är den uppskattade skärningen), $\lambda _{i}$ är krigingvikter som bestäms av den rumsliga beroendestrukturen för residualen och där $e (\mathbf {s} _{i})$ är restvärdet på plats ${\mathbf {s} }_{i}$ . Regressionskoefficienterna ${\hat {\beta }}_{k}$ kan uppskattas från stickprovet med någon anpassningsmetod, t.ex. vanliga minsta kvadrater (OLS) eller, optimalt, med generaliserade minsta kvadrater (GLS) ):

\mathbf {\hat {\beta }} _{\mathtt {GLS}}=\ vänster(\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {q} \right)^{-\mathbf {1} } \cdot \mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {z}

där $\mathbf {\hat {\beta }} _{\mathtt {GLS}}$ är vektorn för uppskattade regressionskoefficienter, $\mathbf {C}$ är kovariansmatrisen av residualerna är ${\mathbf {q} }$ en matris av prediktorer vid samplingsplatserna och $\mathbf {z}$ är vektorn för uppmätta värden för målvariabeln. GLS-uppskattningen av regressionskoefficienter är i själva verket ett specialfall av den geografiskt viktade regressionen. I fallet bestäms vikterna objektivt för att ta hänsyn till den rumsliga autokorrelationen mellan residualerna.

När den deterministiska delen av variationen har uppskattats (regression-del), kan residuet interpoleras med kriging och läggas till den uppskattade trenden. Uppskattningen av residualerna är en iterativ process: först uppskattas den deterministiska delen av variationen med OLS, sedan används kovariansfunktionen för residualerna för att erhålla GLS-koefficienterna. Därefter används dessa för att räkna om residualerna, från vilka en uppdaterad kovariansfunktion beräknas, och så vidare. Även om detta rekommenderas av många geostatistiker som det korrekta förfarandet, visade Kitanidis (1994) att användningen av kovariansfunktionen härledd från OLS-resterna (dvs en enda iteration) ofta är tillfredsställande, eftersom den inte skiljer sig tillräckligt mycket från funktionen som härleds efter flera iterationer; dvs det påverkar inte mycket de slutliga förutsägelserna. Minasny och McBratney (2007) rapporterar liknande resultat – det verkar som att det är viktigare att använda mer data av högre kvalitet än att använda mer sofistikerade statistiska metoder.

I matrisnotation skrivs regression-kriging vanligtvis som:

{\hat {z}}_{\mathtt {RK}}( \mathbf {s} _{0})=\mathbf {q} _{\mathbf {0} }^{\mathbf {T} }\cdot \mathbf {\hat {\beta }} _{\mathtt {GLS }}+\mathbf {\lambda } _{\mathbf {0} }^{\mathbf {T} }\cdot (\mathbf {z} -\mathbf {q} \cdot \mathbf {\hat {\beta } } _{\mathtt {GLS}})

där ${\hat {z}}({\mathbf {s} }_{0})$ är det förutsagda värdet på plats ${\mathbf {s} }_{0 }$ , ${\mathbf {q} }_{\mathbf {0} }$ är vektorn för $p+1$ prediktorer och $\mathbf {\lambda } _ {\mathbf {0} }$ är vektorn för $n$ krigingvikter som används för att interpolera residualerna. RK-modellen anses vara den bästa linjära prediktorn för rumsliga data . Den har en förutsägelsevarians som återspeglar positionen för nya platser (extrapolering) i både geografiskt och funktionsutrymme:

{\hat {\sigma }}_{\mathtt {RK}}^{2}(\mathbf {s} _{0})=( C_{0}+C_{1})-\mathbf {c} _{\mathbf {0} }^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {c} _{\mathbf {0} }+\left(\mathbf {q} _{\mathbf {0} }-\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C } ^{-\mathbf {1} }\cdot \mathbf {c} _{\mathbf {0} }\right)^{\mathbf {T} }\cdot \left(\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {q} \right)^{\mathbf {-1} }\cdot \left(\mathbf {q} _ {\mathbf {0} }-\mathbf {q} ^{\mathbf {T} }\cdot \mathbf {C} ^{-\mathbf {1} }\cdot \mathbf {c} _{\mathbf {0 } }\höger)

där $C_{0}+C_{1}$ är tröskelvarianten och ${\mathbf {c} }_{0}$ är vektorn av kovarianser av residualer på den obesökta platsen .

Beslutsträd för att välja en lämplig rumslig prediktionsmodell.

Många (geo)statistiker tror att det bara finns en bästa linjära opartiska förutsägelsemodell för rumslig data (t.ex. regression-kriging), alla andra tekniker såsom vanlig kriging, miljökorrelation, medelvärdesberäkning av värden per polygon eller invers avståndsinterpolation kan ses som dess speciella fall. Om residualerna inte visar någon rumslig autokorrelation (ren nugget-effekt), konvergerar regression-krigingen till ren multipel linjär regression, eftersom kovariansmatrisen ( ${\displaystyle \mathbf {C} } )$ blir en identitetsmatris. På samma sätt, om målvariabeln inte visar någon korrelation med hjälpprediktorerna, reduceras regression-kriging-modellen till vanlig kriging-modell eftersom den deterministiska delen är lika med det (globala) medelvärdet. Därför bör ren kriging och ren regression endast betraktas som speciella fall av regression-kriging (se figur).

RK och UK/KED

Den geostatistiska litteraturen använder många olika termer för vad som i huvudsak är samma eller åtminstone mycket lika tekniker. Detta förvirrar användarna och distraherar dem från att använda rätt teknik för sina kartläggningsprojekt. Faktum är att både universell kriging, kriging med extern drift och regression-kriging är i princip samma teknik.

Matheron (1969) kallade ursprungligen tekniken Le krigeage universel , men tekniken var tänkt som ett generaliserat fall av kriging där trenden modelleras som en funktion av koordinater. Således reserverar många författare termen universal kriging (UK) för fallet när endast koordinaterna används som prediktorer. Om den deterministiska delen av variation ( drift ) definieras externt som en linjär funktion av vissa hjälpvariabler, snarare än koordinaterna, är termen kriging med extern drift (KED) att föredra (enligt Hengl 2007, "About regression-kriging: From ekvationer till fallstudier"). I fallet med UK eller KED görs förutsägelserna som med kriging, med skillnaden att kovariansmatrisen för residualer utökas med hjälpprediktorerna. Avdriften och residualerna kan dock också uppskattas separat och sedan summeras. Denna procedur föreslogs av Ahmed et al. (1987) och Odeh et al. (1995) kallade det senare för regression-kriging , medan Goovaerts (1997) använder termen kriging med en trendmodell för att hänvisa till en familj av interpolatorer, och refererar till RK som enkel kriging med varierande lokala medel . Minasny och McBratney (2007) kallar helt enkelt denna teknik Empirical Best Linear Unbiased Predictor dvs E-BLUP .

När det gäller KED görs förutsägelser på nya platser av:

{\hat {z}}_{\mathtt {KED}}(\mathbf { s} _{0})=\summa \limits _{i=1}^{n}w_{i}^{\mathtt {KED}}(\mathbf {s} _{0})\cdot z(\ mathbf {s} _{i})

för

\sum \limits _{i=1}^{n}w_{i}^{\ mathtt {KED}}(\mathbf {s} _{0})\cdot q_{k}(\mathbf {s} _{i})=q_{k}(\mathbf {s} _{0})

för $k=1,\ldots ,p$ eller i matrisnotation:

{\hat {z}}_{\mathtt {KED}}(\mathbf {s} _{0})=\mathbf {\delta } _ {\mathbf {0} }^{\mathbf {T} }\cdot \mathbf {z}

där $z$ är målvariabeln, $q_{k}$ s är prediktorvariablerna, dvs värden på en ny plats ( $\displaystyle ({\mathbf {s} }_{ 0})}$ , ${\mathbf {\delta } }_{\mathbf {0} }$ är vektorn för KED-vikter ( $w_{i}^{\mathtt { KED}}$ ), $p$ är antalet prediktorer och $\mathbf {z}$ är vektorn för $n$ observationer på primära platser. KED-vikterna löses med hjälp av de utökade matriserna:

\mathbf {\lambda } _{\mathbf {0} }^{\mathtt {KED}}=\left\{w_{1}^{\mathtt {KED}}(\mathbf {s} _{0}),\ldots ,w_{n}^{\mathtt {KED}}(\mathbf {s} _{0}),\varphi _{0}(\mathbf {s} _{0}) ,\ldots ,\varphi _{p}(\mathbf {s} _{0})\right\}^{\mathbf {T} }=\mathbf {C} ^{{\mathtt {KED}}-1 }\cdot \mathbf {c} _{\mathbf {0} }^{\mathtt {KED}}

där ${\mathbf {\lambda } }_{\mathbf {0} }^{\mathtt {KED}}$ är vektorn för lösta vikter, $\varphi _{p }$ är Lagrange-multiplikatorerna, ${\mathbf {C} }^{\mathtt {KED}}$ är den utökade kovariansmatrisen av residualer och ${\mathbf {c } }_{\mathbf {0} }^{\mathtt {KED}}$ är den utökade vektorn av kovarianser på ny plats.

I fallet med KED ser den utökade kovariansmatrisen av residualer ut så här (Webster och Oliver, 2007; s. 183):

\mathbf {C} ^{\mathtt {KED}}=\left[{\begin{array}{ccccccc}C(\mathbf {s} _{1 },\mathbf {s} _{1})&\cdots &C(\mathbf {s} _{1},\mathbf {s} _{n})&1&q_{1}(\mathbf {s} _{1 })&\cdots &q_{p}(\mathbf {s} _{1})\\\vdots &&\vdots &\vdots &\vdots &&\vdots \\C(\mathbf {s} _{n}, \mathbf {s} _{1})&\cdots &C(\mathbf {s} _{n},\mathbf {s} _{n})&1&q_{1}(\mathbf {s} _{n}) &\cdots &q_{p}(\mathbf {s} _{n})\\1&\cdots &1&0&0&\cdots &0\\q_{1}(\mathbf {s} _{1})&\cdots &q_{1 }(\mathbf {s} _{n})&0&0&\cdots &0\\\vdots &&\vdots &\vdots &\vdots &&\vdots \\q_{p}(\mathbf {s} _{1})& \cdots &q_{p}(\mathbf {s} _{n})&0&0&\cdots &0\end{array}}\right]

och $\mathbf {c} _{\mathbf {0} }^{\mathtt {KED}}$ så här:

\mathbf {c} _{\mathbf {0} }^{\mathtt {KED}}=\left\{C(\mathbf {s} _{0},\mathbf { s} _{1}),\ldots ,C(\mathbf {s} _{0},\mathbf {s} _{n}),q_{0}(\mathbf {s} _{0}), q_{1}(\mathbf {s} _{0}),\ldots ,q_{p}(\mathbf {s} _{0})\right\}^{\mathbf {T} };q_{0 }(\mathbf {s} _{0})=1

Därför ser KED exakt ut som vanlig kriging, förutom att kovariansmatrisen/vektorn utökas med värden på hjälpprediktorer.

Även om KED vid första anblicken verkar vara beräkningsmässigt enklare än RK, måste parametrarna för variogrammet för KED också uppskattas från regressionsrester, vilket kräver ett separat regressionsmodelleringssteg. Denna regression bör vara GLS på grund av den troliga rumsliga korrelationen mellan residualer. Observera att många analytiker istället använder OLS-resterna, som kanske inte skiljer sig alltför mycket från GLS-resterna. De är dock inte optimala om det finns någon rumslig korrelation, och de kan faktiskt vara ganska olika för klustrade sampelpunkter eller om antalet sampel är relativt litet (≪ $\displaystyle \ll 200})$ .

En begränsning av KED är instabiliteten hos den utökade matrisen i det fall att kovariaten inte varierar jämnt i rymden. RK har fördelen att den explicit separerar trenduppskattning från rumslig förutsägelse av residualer, vilket tillåter användning av godtyckligt komplexa former av regression, snarare än de enkla linjära teknikerna som kan användas med KED. Dessutom tillåter den separat tolkning av de två interpolerade komponenterna. Betoningen på regression är också viktig eftersom anpassning av den deterministiska delen av variationen (regression) ofta är mer fördelaktig för kvaliteten på slutkartor än anpassning av den stokastiska delen (rester).

Programvara för att köra regression-kriging

Exempel på ett generiskt ramverk för rumslig förutsägelse av jordvariabler baserat på regression-kriging.

Regression-kriging kan automatiseras t.ex. i R statistisk datormiljö , genom att använda gstat och/eller geoR-paket. Typiska ingångar/utgångar inkluderar:

INGÅNGAR:

Interpolationsuppsättning (punktkarta) — $z(\mathbf {s} _{i})$ $i=1,\ldots ,n$ på primära platser ;
Minsta och maximala förväntade värden och mätprecision ( ${\displaystyle \Delta z} )$ ;
Kontinuerliga prediktorer (rasterkarta) — $q(\mathbf {s} )$ ; på nya obesökta platser
Diskreta prediktorer (polygonkarta);
Valideringsuppsättning (punktkarta) — $z*(\mathbf {s} _{j})$ $j=1,\ldots ,l$ ( frivillig);
Lagavstånd och begränsande avstånd (krävs för att passa variogrammet);

UTGÅNGAR:

Karta över förutsägelser och relativa förutsägelsefel;
Bästa delmängd av prediktorer och korrelationssignifikans (justerad R-kvadrat);
Variogrammodellparametrar (t.ex. $C_{0}$ , $C_{1}$ , $R$ )
GLS-driftmodellkoefficienter;
Prediktionens noggrannhet vid valideringspunkter: medelförutsägelsefel (MPE) och rotmedelkvadratförutsägelsefel (RMSPE);

Tillämpning av regression-kriging

Regression-kriging används inom olika tillämpade områden, från meteorologi, klimatologi, markkartering, geologisk kartläggning, artutbredningsmodellering och liknande. Det enda kravet för att använda regression-kriging jämfört med t.ex. vanlig kriging är att ett eller flera kovariata lager existerar, och som är signifikant korrelerade med funktionen av intresse. Några allmänna tillämpningar av regression-kriging är:

Geostatistisk kartläggning: Regression-kriging tillåter användning av hybrid geostatistiska tekniker för att modellera t.ex. rumslig fördelning av markegenskaper.
Nedskalning av kartor: Regression-kriging kan användas som ett ramverk för att nedskala olika befintliga rutnätskartor. I detta fall måste de kovariata lagren vara tillgängliga med bättre upplösning (vilket motsvarar samplingsintensiteten) än de ursprungliga punktdata.
Felutbredning : Simulerade kartor som genererats med hjälp av en regressions-kriging-modell kan användas för scenarietester och för att uppskatta spridd osäkerhet.

Simuleringar av zinkkoncentrationer härledda med hjälp av en regression-Kriging-modell. Denna modell använder en kontinuerlig (avstånd till floden) och en kategorisk (översvämningsfrekvens) kovariat. Koden som används för att producera dessa kartor finns tillgänglig här .

Regression-kriging-baserade algoritmer spelar en allt viktigare roll i geostatistik eftersom antalet möjliga kovariater ökar varje dag. Till exempel DEM nu tillgängliga från ett antal källor. Detaljerade och exakta bilder av topografi kan nu beställas från fjärranalyssystem som SPOT och ASTER ; SPOT5 erbjuder High Resolution Stereoscopic (HRS) skannern, som kan användas för att producera DEM med upplösningar på upp till 5 m. Finare höjdskillnader kan också erhållas med luftburna laserskannrar. Kostnaden för data är antingen gratis eller sjunker i pris när tekniken utvecklas. NASA registrerade det mesta av världens topografi i Shuttle Radar Topographic Mission år 2000. Från sommaren 2004 har dessa data varit tillgängliga (t.ex. via USGS ftp ) för nästan hela jordklotet med en upplösning på cirka 90 m (för den nordamerikanska kontinenten i upplösning) ca 30 m). Likaså MODIS multispektrala bilder fritt tillgängliga för nedladdning i upplösningar på 250 m. Ett stort gratis arkiv med Landsat-bilder finns också tillgängligt för nedladdning via Global Land Cover Facility ( GLCF).

^ ^a ^b Pebesma, Edzer J (1 juli 2006). "Rollen för externa variabler och GIS-databaser i geostatistisk analys" ( PDF) . Transaktioner i GIS . 10 (4): 615–632. doi : 10.1111/j.1467-9671.2006.01015.x . S2CID 22146107 .
^ Matheron, Georges (1969). "Del 1 av Cahiers du Centre de morphologie mathématique de Fontainebleau". Le krigeage universel . École nationale supérieure des mines de Paris.
^ Cressie, Noel (2012). Statistik för tidsrumsdata . Hoboken, NJ: Wiley. ISBN 9780471692744 .
^ ^a ^b Minasny, Budiman; McBratney, Alex B. (31 juli 2007). "Spatial förutsägelse av markegenskaper med hjälp av EBLUP med Matérn-kovariansfunktionen". Geoderma . 140 (4): 324–336. Bibcode : 2007Geode.140..324M . doi : 10.1016/j.geoderma.2007.04.028 .
^ ^a ^b Christensen, Ronald (2001). Avancerad linjär modellering: multivariat, tidsserier och rumsliga data; icke-parametrisk regression och responsytemaximering (2. ed.). New York, NY [ua]: Springer. ISBN 9780387952963 .
^ Goldberger, AS (1962). "Bästa linjära opartiska förutsägelse i den generaliserade linjära regressionsmodellen". Journal of the American Statistical Association . 57 (298): 369–375. doi : 10.1080/01621459.1962.10480665 . JSTOR 2281645 .
^ Ahmed, Shakeel; De Marsily, Ghislain (1 januari 1987). "Jämförelse av geostatistiska metoder för att uppskatta transmissivitet med hjälp av data om transmissivitet och specifik kapacitet". Vattenresursforskning . 23 (9): 1717. Bibcode : 1987WRR....23.1717A . doi : 10.1029/WR023i009p01717 .
^ Odeh, IOA; McBratney, AB; Chittleborough, DJ (31 juli 1995). "Ytterligare resultat på förutsägelse av markegenskaper från terrängattribut: heterotopisk cokriging och regression-kriging". Geoderma . 67 (3–4): 215–226. Bibcode : 1995Geode..67..215O . doi : 10.1016/0016-7061(95)00007-B .
^ ^a ^b Hengl, Tomislav; Heuvelink, Gerard BM; Stein, Alfred (30 april 2004). "Ett generiskt ramverk för rumslig förutsägelse av jordvariabler baserat på regression-kriging" ( PDF) . Geoderma . 120 (1–2): 75–93. Bibcode : 2004Geode.120...75H . doi : 10.1016/j.geoderma.2003.08.018 .
^ Webster, Richard; Oliver, Margaret A. (2007). Geostatistik för miljövetare (2:a uppl.). Chichester: Wiley. ISBN 9780470028582 .
^ Hengl, Tomislav; Bajat, Branislav; Blagojević, Dragan; Reuter, Hannes I. (1 december 2008). "Geostatistisk modellering av topografi med hjälp av hjälpkartor" (PDF) . Datorer & geovetenskap . 34 (12): 1886–1899. Bibcode : 2008CG.....34.1886H . doi : 10.1016/j.cageo.2008.01.005 .
^ Toutin, Thierry (30 april 2006). "Generering av DSM från SPOT-5 in-track HRS och cross-track HRG stereodata med hjälp av spatiotriangulering och autokalibrering". ISPRS Journal of Photogrammetry and Remote Sensing . 60 (3): 170–181. Bibcode : 2006JPRS...60..170T . doi : 10.1016/j.isprsjprs.2006.02.003 .
^ Rabus, Bernhard; Eineder, Michael; Roth, Achim; Bamler, Richard (31 januari 2003). "Radartopografiuppdraget för skytteln - en ny klass av digitala höjdmodeller som förvärvats av rymdburen radar". ISPRS Journal of Photogrammetry and Remote Sensing . 57 (4): 241–262. Bibcode : 2003JPRS...57..241R . doi : 10.1016/S0924-2716(02)00124-7 .

Vidare läsning

Kapitel 2, Regression-kriging , i Tomislav Hengl (2009), A Practical Guide to Geostatistical Mapping , 291 s., ISBN 978-90-9024981-0 . [1]
Hengl T., Heuvelink GBM, Rossiter DG (2007). "Om regression-kriging: från ekvationer till fallstudier". Datorer & Geovetenskap . 33 (10): 1301–1315. Bibcode : 2007CG.....33.1301H . doi : 10.1016/j.cageo.2007.05.001 . {{ citera journal }} : CS1 underhåll: använder författarens parameter ( länk )

externa länkar

Gstat- paket (implementerar KED)
GeoR- paket (implementerar KED)

[Pebesma2006IJGIS-1] Pebesma, Edzer J (1 juli 2006). "Rollen för externa variabler och GIS-databaser i geostatistisk analys" ( PDF) . Transaktioner i GIS . 10 (4): 615–632. doi : 10.1111/j.1467-9671.2006.01015.x . S2CID 22146107 .

[2] Matheron, Georges (1969). "Del 1 av Cahiers du Centre de morphologie mathématique de Fontainebleau". Le krigeage universel . École nationale supérieure des mines de Paris.

[Cressie2012Wiley-3] Cressie, Noel (2012). Statistik för tidsrumsdata . Hoboken, NJ: Wiley. ISBN 9780471692744 .

[MinasnyMcBratney2007Geoderma-4] Minasny, Budiman; McBratney, Alex B. (31 juli 2007). "Spatial förutsägelse av markegenskaper med hjälp av EBLUP med Matérn-kovariansfunktionen". Geoderma . 140 (4): 324–336. Bibcode : 2007Geode.140..324M . doi : 10.1016/j.geoderma.2007.04.028 .

[Christensen2001Springer-5] Christensen, Ronald (2001). Avancerad linjär modellering: multivariat, tidsserier och rumsliga data; icke-parametrisk regression och responsytemaximering (2. ed.). New York, NY [ua]: Springer. ISBN 9780387952963 .

[Goldberger1962-6] Goldberger, AS (1962). "Bästa linjära opartiska förutsägelse i den generaliserade linjära regressionsmodellen". Journal of the American Statistical Association . 57 (298): 369–375. doi : 10.1080/01621459.1962.10480665 . JSTOR 2281645 .

[7] Ahmed, Shakeel; De Marsily, Ghislain (1 januari 1987). "Jämförelse av geostatistiska metoder för att uppskatta transmissivitet med hjälp av data om transmissivitet och specifik kapacitet". Vattenresursforskning . 23 (9): 1717. Bibcode : 1987WRR....23.1717A . doi : 10.1029/WR023i009p01717 .

[Odeh1995-8] Odeh, IOA; McBratney, AB; Chittleborough, DJ (31 juli 1995). "Ytterligare resultat på förutsägelse av markegenskaper från terrängattribut: heterotopisk cokriging och regression-kriging". Geoderma . 67 (3–4): 215–226. Bibcode : 1995Geode..67..215O . doi : 10.1016/0016-7061(95)00007-B .

[Hengl2004Geoderma-9] Hengl, Tomislav; Heuvelink, Gerard BM; Stein, Alfred (30 april 2004). "Ett generiskt ramverk för rumslig förutsägelse av jordvariabler baserat på regression-kriging" ( PDF) . Geoderma . 120 (1–2): 75–93. Bibcode : 2004Geode.120...75H . doi : 10.1016/j.geoderma.2003.08.018 .

[WebsterOliver2007-10] Webster, Richard; Oliver, Margaret A. (2007). Geostatistik för miljövetare (2:a uppl.). Chichester: Wiley. ISBN 9780470028582 .

[Hengl2008CG-11] Hengl, Tomislav; Bajat, Branislav; Blagojević, Dragan; Reuter, Hannes I. (1 december 2008). "Geostatistisk modellering av topografi med hjälp av hjälpkartor" (PDF) . Datorer & geovetenskap . 34 (12): 1886–1899. Bibcode : 2008CG.....34.1886H . doi : 10.1016/j.cageo.2008.01.005 .

[12] Toutin, Thierry (30 april 2006). "Generering av DSM från SPOT-5 in-track HRS och cross-track HRG stereodata med hjälp av spatiotriangulering och autokalibrering". ISPRS Journal of Photogrammetry and Remote Sensing . 60 (3): 170–181. Bibcode : 2006JPRS...60..170T . doi : 10.1016/j.isprsjprs.2006.02.003 .

[13] Rabus, Bernhard; Eineder, Michael; Roth, Achim; Bamler, Richard (31 januari 2003). "Radartopografiuppdraget för skytteln - en ny klass av digitala höjdmodeller som förvärvats av rymdburen radar". ISPRS Journal of Photogrammetry and Remote Sensing . 57 (4): 241–262. Bibcode : 2003JPRS...57..241R . doi : 10.1016/S0924-2716(02)00124-7 .