Regge–Wheeler–Zerilli ekvationer

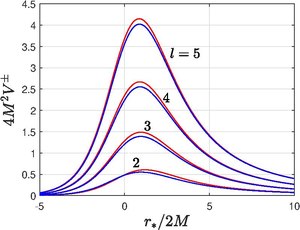
Röda linjer: Regge-Wheeler potentialer. Blå linjer: Zerilli potentialer

I allmän relativitetsteori är Regge–Wheeler–Zerilli-ekvationer ett par ekvationer som beskriver gravitationsstörningar av ett svart hål från Schwarzschild, uppkallat efter Tullio Regge , John Archibald Wheeler och Frank J. Zerilli. Störningarna av en Schwarzchild-metrik klassificeras i två typer, nämligen axiella och polära störningar, en terminologi som introducerades av Subrahmanyan Chandrasekhar . Axiella störningar inducerar ramdragning genom att ge rotationer till det svarta hålet och ändra tecken när den azimutala riktningen vänds, medan polära störningar inte ger rotationer och inte ändrar tecken under omkastningen av azimutriktningen. Ekvationen för axiella störningar kallas Regge–Wheeler-ekvationen och ekvationen som styr polära störningar kallas Zerilli-ekvationen .

Ekvationerna har samma form som den endimensionella Schrödinger-ekvationen . Ekvationerna läses som

$\left({\frac {d^{2}}{dr_{*}^{2}}}+\sigma ^{ 2}\höger)Z^{\pm }=V^{\pm }Z^{\pm }$

där $Z^{+}$ kännetecknar de polära störningarna och $Z^{-}$ de axiella störningarna. Här är $r_{*}=r+2M\ln(r/2M-1)$ sköldpaddans koordinat (vi sätter $G=c=1$ ), $r$ tillhör Schwarzschild-koordinaterna $(t,r,\theta ,\varphi )$ , $2M$ är Schwarzschild-radien och $\sigma$ representerar tidsberoendet för de störningar som uppträder i formen $e^{i\sigma t}$ . Regge–Wheeler potentialen och Zerilli potentialen ges av

$V^{-}={\frac {2(r^{2}-2Mr)}{ r^{5}}}[(n+1)r-3M]$

$V^{+}={\frac {2(r^{2}-2Mr)}{r^{5}(nr +3M)^{2}}}[n^{2}(n+1)r^{3}+3Mn^{2}r^{2}+9M^{2}nr+9M^{3}]$

där $2n=(l-1)(l+2)$ och $l=2,3,4 ,\dots$ kännetecknar egenmoden för $\theta$ -koordinaten. För gravitationsstörningar är moden $l=0,\,1$ irrelevanta eftersom de inte utvecklas med tiden. Fysiskt gravitationsstörningar med $l=0$ (monopol)-läge representerar en förändring i det svarta hålets massa, medan $l=1$ (dipol)-läget motsvarar en förskjutning i läget och värdet av det svarta hålets rörelsemängd. Formen på ovanstående potentialer visas i figuren.

Kom ihåg att i sköldpaddans koordinat, $r_{*}\rightarrow -\infty$ anger händelsehorisont och $r_{*}\rightarrow \infty$ är ekvivalent med $r\rightarrow \infty$ dvs till avstånd långt bort från det bakre hålet. Potentialerna har kort räckvidd eftersom de avtar snabbare än $1/r_{*}$ ; som $r_{*}\rightarrow \infty$ , har vi $V^{\pm }\rightarrow 2(n+1)/ r^{2}$ och som $r_{*}\rightarrow -\infty$ , har vi $V^{\pm }\sim e^{r_{*}/2M}.$ Följaktligen, det asymptotiska beteendet hos lösningarna för $r_{*}\rightarrow \pm \infty$ är $e^{\pm i\sigma r_{*}}.$

Relationer mellan de två problemen

1975 upptäckte Subrahmanyan Chandrasekhar och Steven Detweiler en en-till-en-mappning mellan de två ekvationerna, vilket ledde till en konsekvens att spektrumet som motsvarar båda potentialerna är identiskt. De två potentialerna kan också skrivas som

$V^{\pm }=\pm 6M{\frac {df}{dr_{*}}}+(6Mf)^{2}+4n(n+1)f,\quad f={\frac {r^{2}-2Mr}{2r^{3}(nr+3M)}}.$

Relationerna mellan $Z^{+}$ och $Z^{-}$ ges av

$[4n(n+1)\pm 12i\sigma M]Z^{\pm }=\left[4n(n+1)+{\frac {72M^{2}(r^{2}- 2Mr)}{r^{3}(2nr+6M)}}\right]Z^{\mp }\pm 12M{\frac {dZ^{\mp }}{dr_{*}}}.$

Reflektion och transmissionskoefficienter

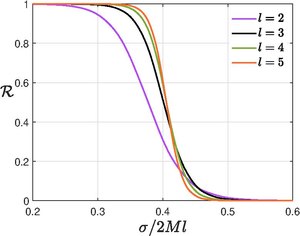
Reflektionskoefficienter på grund av Regge-Wheeler-Zerilli potentialer

Här är $V^{\pm }$ alltid positiv och problemet är ett av reflektion och överföring av vågor som infaller från $r_{*}\rightarrow \infty$ till $r_{*}\rightarrow -\infty$ . Problemet är i huvudsak detsamma som ett reflektions- och transmissionsproblem genom en potentiell barriär inom kvantmekaniken. Låt den infallande vågen med enhetsamplitud vara ${\displaystyle e^{+i\sigma r_{*}}},$ då ges lösningens asymptotiska beteende av

$Z^{\pm }=e^{+i\sigma r_{*}}+R^{ \pm }e^{-i\sigma r_{*}}\quad {\text{as}}\quad r_{*}\rightarrow +\infty$

$Z^{\pm }=T^{\pm }e^{i\sigma r_{*}}\quad {\text{as}}\quad r_{*}\rightarrow -\infty$

där $R=R(\sigma )$ och $T=T(\sigma )$ är reflektions- och transmissionsamplituderna. I den andra ekvationen har vi ställt det fysiska kravet att inga vågor kommer ut från händelsehorisonten.

Reflexions- och transmissionskoefficienterna definieras således som

${\mathcal {R}}^{\pm }=|R^{\pm }|^{2},\quad {\mathcal {T}}^{\pm }=|T^{\ pm }|^{2}$

utsätts för villkoret ${\mathcal {R}}^{\pm }+{\mathcal {T}}^{\pm }=1.$ På grund av den inneboende kopplingen mellan de två ekvationerna som skisserades i föregående avsnitt, visar det sig

$T^{+ }=T^{-},\quad R^{+}=e^{i\delta}R^{-},\quad e^{i\delta}={\frac {4n(n+1)- 12i\sigma M}{4n(n+1)+12i\sigma M}}$

och följaktligen, eftersom $R^{+}$ och $R^{-}$ endast skiljer sig åt i sina faser, får vi

${\mathcal {T}}\equiv {\mathcal {T}}^{+}={\mathcal {T}}^{-},\quad {\mathcal {R}}\equiv {\mathcal {R}}^{+}={\mathcal {R}}^{-}.$

Kvasinormala lägen

Kvasinormala lägen motsvarar rena toner i det svarta hålet. Den beskriver för godtyckliga, men små, störningar såsom ett föremål som faller in i det svarta hålet, ansamling av materia som omger det, sista stadiet av lätt asfärisk kollaps etc. Störningar är av dämpande typ och motsvarar därför komplexa värden på σ {\ $\ sigma }$ . De erforderliga gränsvillkoren är

$Z^{\pm }=A^{\pm }e^{-i\sigma r_{*}}\quad {\text {as}}\quad r_{*}\rightarrow +\infty$

$Z^{\pm }=e^{i\sigma r_{*} }\quad {\text{as}}\quad r_{*}\rightarrow -\infty$

vilket indikerar att vi har rent utgående vågor med amplitud $A^{\pm }$ och rent ingående vågor vid horisonten.

Problemet blir ett egenvärdeproblem. Återigen på grund av förhållandet som nämns mellan de två problemen, är spektrumet för $Z^{+}$ och $Z^{-}$ identiska och det räcker därför att beakta spektrumet för $Z^{-}.$ Problemet förenklas genom att introducera

$Z^{-}=\exp \left(i\int ^{r_{*}}\phi \,dr_{*}\right).$

Det olinjära egenvärdesproblemet ges av

$i{\frac {d\phi }{dr_{*}}}+\sigma ^{2}-\phi ^{2}-V^{-}=0,\quad \phi (-\infty )=+\sigma ,\quad \phi (+\infty )=-\sigma .$

Lösningen finns endast för en diskret uppsättning värden på $\sigma .$