Quickhull

Quickhull är en metod för att beräkna det konvexa skrovet av en ändlig uppsättning punkter i n -dimensionell rymd. Den använder en dela och erövra -metod som liknar den för quicksort , som dess namn kommer från. Dess värsta komplexitet för 2-dimensionell och 3-dimensionell rymd anses vara $O(n\log(r))$ , där $n$ är talet av inmatningspunkter och $r$ är antalet bearbetade punkter. Men till skillnad från quicksort finns det inget självklart sätt att konvertera quickhull till en randomiserad algoritm. Ändå finns det verk från Smoothed Analysis som berättar att den 2-dimensionella Quick-skrovsalgoritmen har förväntat körtid $O(n\log(n))$ . Faktum är att och relaterade arbeten visar att antalet punkter på det konvexa skrovet för varje slumpmässigt störd punkter med Gaussiskt brus är $O({\sqrt {\log n}})$ som det följer av att Quick hull (och många andra algoritmer) bara kan ta $O(n{\sqrt {\log n}})$ tid på vilken som helst uppsättning störda punkter.

N-dimensionell Quickhull uppfanns 1996 av C. Bradford Barber, David P. Dobkin och Hannu Huhdanpaa. Det var en förlängning av Jonathan Scott Greenfields plana Quickhull-algoritm från 1990, även om författarna från 1996 inte kände till hans metoder. Istället beskriver Barber et al det som en deterministisk variant av Clarkson och Shors algoritm från 1989.

Den här animationen skildrar quickhull-algoritmen.

Algoritm

Steg 1-2: Dela poäng i två delmängder

Under genomsnittliga omständigheter fungerar algoritmen ganska bra, men bearbetningen blir vanligtvis långsam i fall av hög symmetri eller punkter som ligger på en cirkels omkrets. Algoritmen kan delas upp i följande steg:

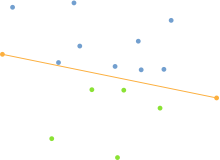
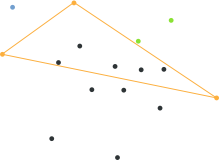
1. Hitta punkterna med minimum och maximum x-koordinater, eftersom dessa alltid kommer att vara en del av det konvexa skrovet. Om det finns många punkter med samma minimum/högsta x, använd de med minsta/högsta y på motsvarande sätt.
2. Använd linjen som bildas av de två punkterna för att dela upp mängden i två delmängder av punkter, som kommer att bearbetas rekursivt.
3. Bestäm punkten, på ena sidan av linjen, med det maximala avståndet från linjen. Denna punkt bildar en triangel med linjens.
4. Punkterna som ligger inuti den triangeln kan inte vara en del av det konvexa skrovet och kan därför ignoreras i nästa steg.
5. Upprepa de två föregående stegen på de två linjerna som bildas av triangeln (inte den första linjen).
6. Fortsätt göra så tills inga fler punkter finns kvar, rekursionen har kommit till ett slut och de valda punkterna utgör det konvexa skrovet.

Steg 3-5: Hitta maximal avståndspunkt, ignorera punkter inuti triangeln och upprepa det

Steg 6: Återgå tills inga fler poäng finns kvar

Problemet är mer komplext i det högre dimensionella fallet, eftersom skrovet är byggt av många aspekter; datastrukturen måste ta hänsyn till det och registrera linjen/planet/hyperplanet (ryggen) som delas av angränsande aspekter också. För d -mått:

1. Välj d + 1 poäng från uppsättningen som inte delar ett plan eller ett hyperplan. Detta bildar ett initialt skrov med fasetter Fs[] .
2. För varje F i Fs[] , hitta alla otilldelade punkter som är "ovanför" det, dvs pekar bort från centrum av skrovet, och lägg till det till en "utanför" uppsättning FO som är associerad med F .
3. För varje F med en icke-tom FO :
   1. Hitta punkten p med det maximala avståndet från F . Vi kommer att lägga till det i skrovet.
   2. Skapa en synlig uppsättning V och initialisera den till F . Förläng V i alla riktningar för angränsande fasetter Fv tills inga ytterligare fasetter är synliga från p . Att Fv är synligt från p betyder att p är över Fv
   3. Gränsen för V bildar då uppsättningen av horisontryggar H .
   4. Låt Fnew[] vara uppsättningen av fasetter skapade av p och alla åsar i H .
   5. För varje ny aspekt i Fnew[] , utför steg (2) och initiera sina egna externa uppsättningar. Den här gången titta bara från punkter som ligger utanför en fasett i V med deras yttre mängder V[i].O , eftersom vi bara har expanderat i den riktningen.
   6. Ta bort de nu interna aspekterna i V från Fs[] . Lägg till de nya aspekterna i Fnew[] till Fs[] och fortsätt iterationen.

Pseudokod för 2D-uppsättning punkter

    


     
    
     
         Ingång = en mängd S av n punkter Antag att det finns minst 2 punkter i ingångsmängden S av punkter  funktion  QuickHull(  S  )  är  // Hitta konvext skrov från mängden S av n punkter  Convex Hull := {} Hitta vänster och höger de flesta punkterna, säg A & B, och lägg till A & B till det konvexa skrovet Segment AB delar upp de återstående (  n  − 2) punkterna i 2 grupper  S1  och  S2  där  S1  är punkter i  S  som ligger på höger sida av den orienterade linjen från  A  till  B  , och  S2  är punkter i  S  som ligger på höger sida av den orienterade linjen från  B  till  A  FindHull(  S1  ,  A  ,  B  ) FindHull(  S2  ,  B  ,  A  ) Output := Convex Hull  end function  function  FindHull (  Sk  ,  P  ,  Q  )  är  // Hitta punkter på konvexa skrov från mängden Sk av punkter  // som är på höger sida av den orienterade linjen från P till Q  om  Sk  inte har någon punkt ,   återvänd  sedan  från den givna uppsättningen punkter i  Sk  , hitta den längsta punkten, säg  C  , från segmentet  PQ  Lägg till punkt  C  till det konvexa skrovet på platsen mellan  P  och  Q  Tre punkter  P  ,  Q  och  C  delar upp de återstående punkterna i  Sk  i 3 delmängder:  S0  ,  S1  och  S2  där  S0  är punkter inuti triangeln PCQ,  S1  är punkter på höger sida av den orienterade linjen från  P  till  C  och  S2  är punkter på höger sida av den orienterade linjen från  C  till  Q  . FindHull(   S1  ,  P  ,  C  ) FindHull(  S2  ,  C  ,  Q  )  slutfunktion 

En pseudokod specialiserad för 3D-fallet finns tillgänglig från Jordan Smith. Den innehåller en liknande strategi för "maximal poäng" för att välja startskrov. Om dessa maximala poäng är degenererade, är hela punktmolnet det också.

Se även

• Konvexa skrovalgoritmer

• Dave Mount. "Föreläsning 3: Fler konvexa skrovalgoritmer" .

externa länkar

• Implementering av QuickHull (GDC 2014) – Algoritmpresentation med 3D-implementeringsdetaljer.