Q-funktion

För fas-rymdfunktionen som representerar ett kvanttillstånd, se Husimi Q-representation .

En plot av Q-funktionen.

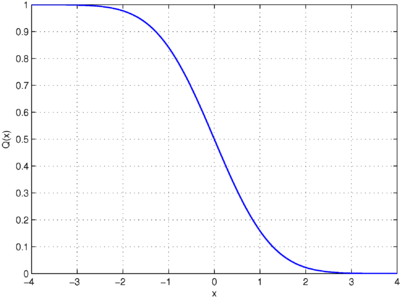
I statistik är Q -funktionen svansfördelningsfunktionen för standardnormalfördelningen . Med andra ord, $Q(x)$ är sannolikheten att en normal (gaussisk) slumpvariabel kommer att få ett värde som är större än $x$ standardavvikelser. På motsvarande sätt $Q(x)$ sannolikheten att en normal normal slumpvariabel tar ett värde som är större än $x$ .

Om $Y$ är en gaussisk slumpvariabel med medelvärde $\mu$ och varians $\sigma ^{2}$ , då $X={\ frac {Y-\mu }{\sigma }}$ är standard normal och

$P(Y>y)=P(X>x)=Q(x)$

där $x={\frac {y-\mu }{\sigma }}$ .

Andra definitioner av Q -funktionen, som alla är enkla transformationer av den normala kumulativa fördelningsfunktionen , används också ibland.

På grund av dess relation till normalfördelningens kumulativa fördelningsfunktion kan Q -funktionen också uttryckas i termer av felfunktionen , som är en viktig funktion i tillämpad matematik och fysik.

Definition och grundläggande egenskaper

Formellt definieras Q -funktionen som

$Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }\exp \left(-{\frac {u^{2} }{2}}\right)\,du.$

Således,

$Q(x)=1-Q(-x)=1-\Phi (x)\,\!,$

där $\Phi (x)$ är den kumulativa fördelningsfunktionen för den normala gaussiska normalfördelningen .

Q - funktionen kan uttryckas i termer av felfunktionen , eller den komplementära felfunktionen, som

${\begin{aligned}Q(x)&={\frac {1}{2}}\left({\frac {2}{\sqrt {\pi }}}\int _{x/{ \sqrt {2}}}^{\infty }\exp \left(-t^{2}\right)\,dt\right)\\&={\frac {1}{2}}-{\frac {1}{2}}\operatörsnamn {erf} \left({\frac {x}{\sqrt {2}}}\right)~~{\text{ -eller-}}\\&={\frac {1}{2}}\operatörsnamn {erfc} \left({\frac {x}{\sqrt {2}}}\right).\end{aligned}}$

En alternativ form av Q -funktionen känd som Craigs formel, efter dess upptäckare, uttrycks som:

$Q(x)={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{ 2}}{2\sin ^{2}\theta }}\right)d\theta .$

Detta uttryck är endast giltigt för positiva värden på x , men det kan användas tillsammans med Q ( x ) = 1 − Q (− x ) för att få Q ( x ) för negativa värden. Denna form är fördelaktig genom att integrationsområdet är fast och ändligt.

Craigs formel utökades senare av Behnad (2020) för Q -funktionen av summan av två icke-negativa variabler, enligt följande:

Q-funktionen plottad i det komplexa planet

$Q(x+y) ={\frac {1}{\pi }}\int _{0}^{\frac {\pi}{2}}\exp \left(-{\frac {x^{2}}{2\sin ^{2}\theta }}-{\frac {y^{2}}{2\cos ^{2}\theta }}\right)d\theta ,\quad x,y\geqslant 0.$

Gränser och approximationer

• Q - funktionen är inte en elementär funktion . Borjesson-Sundbergs gränser, där $\phi (x)$ är densitetsfunktionen för standardnormalfördelningen,

$\left({\frac {x}{1+x^{2}}}\right)\phi (x)<Q(x)<{\frac {\phi (x)}{x}},\qquad x>0,$

blir allt snävare för stora x , och är ofta användbara.

Med hjälp av substitutionen v = u ² /2 härleds den övre gränsen enligt följande:

$Q(x)=\int _{x}^{\infty }\phi (u)\,du<\int _{x}^{\infty }{\frac {u}{x}}\ phi (u)\,du=\int _{\frac {x^{2}}{2}}^{\infty }{\frac {e^{-v}}{x{\sqrt {2\pi }}}}\,dv=-{\biggl .}{\frac {e^{-v}}{x{\sqrt {2\pi }}}}{\biggr |}_{\frac {x^ {2}}{2}}^{\infty }={\frac {\phi (x)}{x}}.$

På liknande sätt använder du $\phi '(u)=-u\phi (u)$ och kvotregeln ,

$\left(1+{\frac {1}{x^{2}}}\right)Q(x)=\int _{x}^{\infty }\left(1+{\frac { 1}{x^{2}}}\right)\phi (u)\,du>\int _{x}^{\infty }\left(1+{\frac {1}{u^{2} }}\right)\phi (u)\,du=-{\biggl .}{\frac {\phi (u)}{u}}{\biggr |}_{x}^{\infty }={ \frac {\phi (x)}{x}}.$

Lösning för Q ( x ) ger den nedre gränsen.

Det geometriska medelvärdet av den övre och nedre gränsen ger en lämplig approximation för $Q(x)$ :

${\displaystyle Q( x)\approx {\frac {\phi (x)}{\sqrt {1+x^{2}}}},\qquad x\geq 0.} Snävare gränser och approximationer av Q ($

• x $Q (x)}$ kan också erhållas genom att optimera följande uttryck

${\tilde {Q}}(x)={\frac {\phi (x)}{(1-a)x+a{\sqrt {x^{2}+b}}}}.$

För $x\geq 0$ ges den bästa övre gränsen av $a=0,344$ och $b=5,334$ med maximalt absolut relativfel på 0,44%. På samma sätt ges den bästa approximationen av $a=0,339$ och $b=5,510$ med maximalt absolut relativfel på 0,27%. Slutligen ges den bästa nedre gränsen av $a=1/\pi$ och $b=2\pi$ med maximalt absolut relativfel på 1,17%.

• Chernoff -gränsen för Q -funktionen är

$Q(x)\leq e^{-{\frac {x^{2}}{2}}} ,\qquad x>0$

• Förbättrade exponentiella gränser och en ren exponentiell approximation är

$Q (x)\leq {\tfrac {1}{4}}e^{-x^{2}}+{\tfrac {1}{4}}e^{-{\frac {x^{2}} {2}}}\leq {\tfrac {1}{2}}e^{-{\frac {x^{2}}{2}}},\qquad x>0$

${\displaystyle Q(x)\approx {\frac {1}{12}}e^{-{\frac {x^{2}} {2}}}+{\frac {1}{4}}e^{-{\frac {2}{3}}x^{2}},\qquad x>0} Ovanstående generaliserades$

• av Tanash & Riihonen (2020), som visade att $Q(x)$ exakt kan approximeras eller avgränsas av

${\tilde {Q}}(x)=\sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.$

De presenterade en systematisk metod för att lösa de numeriska koefficienterna $\{(a_{n},b_{n})\}_{n=1}^{N}$ som ger en minimax approximation eller bunden: $Q(x)\approx {\tilde {Q}}(x)$ , $Q(x)\leq {\tilde {Q}}(x)$ , eller $Q(x)\geq {\tilde {Q}}(x )$ för $x\geq 0$ . Med exemplet koefficienter i tabellform för $N=20$ är de relativa och absoluta approximationsfelen mindre än $2,831\cdot 10^{-6}$ och ${\displaystyle 1.416\cdot 10^{-6}} ,$ respektive. Koefficienterna $\{(a_{n},b_{n})\}_{n=1}^{N}$ för många varianter av exponentialen approximationer och gränser upp till $N=25$ har släppts för att öppna åtkomsten som en omfattande datauppsättning.

• En annan approximation av $Q(x)$ för $x\in [0,\infty )$ ges av Karagiannidis & Lioumpas (2007) som visade för det lämpliga valet av parametrarna $\{A,B\}$ att

$f(x;A,B)={\frac {\left(1-e^{-Ax}\right)e^{-x^{2}}}{B{\sqrt {\pi } }x}}\approx \operatörsnamn {erfc} \left(x\right).$

Det absoluta felet mellan $f(x;A,B)$ och $\operatorname {erfc} (x)$ över intervallet $[0,R]$ minimeras genom att utvärdera

$\{A,B\}={\underset {\{A,B\}}{\arg \min }}{\frac {1}{R}}\int _{0}^{R} |f(x;A,B)-\operatörsnamn {erfc} (x)|dx.$

Genom att använda $R=20$ och numeriskt integrera, fann de att det minsta felet inträffade när $\{A,B\}=\{1.98,1.135\},$ vilket gav en bra approximation för $\forall x\geq 0.$

Ersätter dessa värden och att använda relationen mellan $Q(x)$ och $\operatorname {erfc} (x)$ från ovan ger

${\displaystyle Q(x)\approx {\frac {\left(1-e^{\frac {-1.98x}{\sqrt {2 }}}\right)e^{-{\frac {x^{2}}{2}}}}{1.135{\sqrt {2\pi }}x}},x\geq 0.} Alternativa koefficienter$

är även tillgänglig för ovanstående 'Karagiannidis–Lioumpas approximation' för att skräddarsy noggrannhet för en specifik applikation eller omvandla den till en tight bound.

• En snävare och mer lättillgänglig approximation av $Q(x)$ för positiva argument $x\in [0,\infty )$ ges av López-Benítez & Casadevall ( 2011) baserat på en andra ordningens exponentialfunktion:

$Q(x)\approx e^{-ax^{2}- bx-c},\qquad x\geq 0.$

Passningskoefficienterna $(a,b,c)$ kan optimeras över alla önskade argumentintervall för att minimera summan av kvadratfel ( $a=0,3842$ , $b=0,7640$ , $c=0,6964$ för $x\in [0 ,20]$ ) eller minimera det maximala absoluta felet ( $a=0,4920$ , $b=0,2887$ , ${\displaystyle c=1,1893$$x\in [0,20]$ för ). Denna approximation erbjuder vissa fördelar, såsom en bra avvägning mellan noggrannhet och analytisk följsamhet (till exempel är utvidgningen till valfri godtycklig potens av $Q(x)$ trivial och ändrar inte den algebraiska formen av uppskattningen).

Omvänd Q

Den omvända Q -funktionen kan relateras till de omvända felfunktionerna :

$Q^{-1}(y)={\sqrt {2} }\ \mathrm {erf} ^{-1}(1-2y)={\sqrt {2}}\ \mathrm {erfc} ^{-1}(2y)$

Funktionen $Q^{-1}(y)$ finner tillämpning i digital kommunikation. Det uttrycks vanligtvis i dB och kallas vanligtvis Q-faktor :

$\mathrm {Q{\text{-}}faktor} =20\log _{10}\!\vänster (Q^{-1}(y)\höger)\!~\mathrm {dB}$

där y är bitfelsfrekvensen (BER) för den digitalt modulerade signalen som analyseras. Till exempel, för QPSK i additivt vitt Gaussiskt brus, sammanfaller Q-faktorn definierad ovan med värdet i dB för signal- brusförhållandet som ger en bitfelsfrekvens lika med y .

Q-faktor vs. bitfelsfrekvens (BER).

Värderingar

Q - funktionen är väl tabellerad och kan beräknas direkt i de flesta matematiska mjukvarupaket som R och de som finns tillgängliga i Python , MATLAB och Mathematica . Vissa värden för Q -funktionen ges nedan som referens.

Q (0,0)	0,500000000	1/2.0000
Q (0,1)	0,460172163	1/2.1731
Q (0,2)	0,420740291	1/2,3768
Q (0,3)	0,382088578	1/2,6172
Q (0,4)	0,344578258	1/2.9021
Q (0,5)	0,308537539	1/3.2411
Q (0,6)	0,274253118	1/3,6463
Q (0,7)	0,241963652	1/4.1329
Q (0,8)	0,211855399	1/4.7202
Q (0,9)	0,184060125	1/5,4330

Q (1,0)	0,158655254	1/6.3030
Q (1,1)	0,135666061	1/7,3710
Q (1,2)	0,115069670	1/8.6904
Q (1,3)	0,096800485	1/10.3305
Q (1,4)	0,080756659	1/12.3829
Q (1,5)	0,066807201	1/14.9684
Q (1,6)	0,054799292	1/18.2484
Q (1,7)	0,044565463	1/22.4389
Q (1,8)	0,035930319	1/27.8316
Q (1,9)	0,028716560	1/34.8231

Q (2,0)	0,022750132	1/43.9558
Q (2,1)	0,017864421	1/55.9772
Q (2,2)	0,013903448	1/71.9246
Q (2,3)	0,010724110	1/93.2478
Q (2,4)	0,008197536	1/121,9879
Q (2,5)	0,006209665	1/161.0393
Q (2,6)	0,004661188	1/214.5376
Q (2,7)	0,003466974	1/288.4360
Q (2,8)	0,002555130	1/391.3695
Q (2,9)	0,001865813	1/535.9593

Q (3,0)	0,001349898	1/740.7967
Q (3.1)	0,000967603	1/1033.4815
Q (3,2)	0,000687138	1/1455.3119
Q (3,3)	0,000483424	1/2068.5769
Q (3,4)	0,000336929	1/2967.9820
Q (3,5)	0,000232629	1/4298.6887
Q (3,6)	0,000159109	1/6285.0158
Q (3,7)	0,000107800	1/9276.4608
Q (3,8)	0,000072348	1/13822.0738
Q (3,9)	0,000048096	1/20791.6011
Q (4,0)	0,000031671	1/31574.3855

Generalisering till höga dimensioner

Q - funktionen kan generaliseras till högre dimensioner:

$Q(\mathbf {x} )=\mathbb {P} (\mathbf {X} \geq \mathbf {x} ),$

där $\mathbf {X} \sim {\mathcal {N}}(\mathbf {0} ,\,\Sigma )$ följer den multivariata normalfördelningen med kovarians $\ Sigma$ och tröskeln är av formen $\mathbf {x} =\gamma \Sigma \mathbf {l} ^{*}$$> {\displaystyle \mathbf {l} ^{*}>\mathbf {0} }$ någon positiv vektor och positiv konstant $\gamma >0$ . Som i det endimensionella fallet finns det ingen enkel analytisk formel för Q -funktionen. Ändå kan Q -funktionen approximeras godtyckligt då $\gamma$ blir större och större.