Provtagning av skivor

Slice sampling är en typ av Markov-kedjans Monte Carlo- algoritm för pseudo-slumpmässigt talsampling, dvs för att dra slumpmässiga urval från en statistisk fördelning. Metoden är baserad på observationen att för att ta prov på en slumpvariabel kan man prova enhetligt från regionen under grafen för dess densitetsfunktion.

Motivering

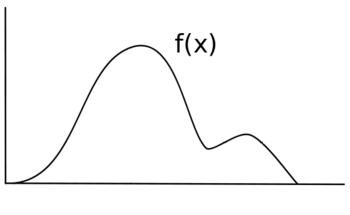
Anta att du vill ta prov på någon slumpvariabel X med fördelningen f ( x ). Antag att följande är grafen för f ( x ). Höjden på f ( x ) motsvarar sannolikheten vid den punkten.

Om du skulle sampla X likformigt , skulle varje värde ha samma sannolikhet att samplas, och din fördelning skulle ha formen f ( x ) = y för något y -värde istället för någon olikformig funktion f ( x ). Istället för den ursprungliga svarta linjen skulle din nya distribution se ut mer som den blå linjen.

För att sampla X på ett sätt som kommer att behålla fördelningen f ( x ), måste någon samplingsteknik användas som tar hänsyn till de varierande sannolikheterna för varje område av f ( x ).

Metod

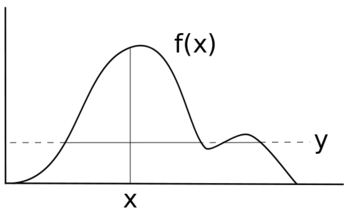
Skär provtagning, i sin enklaste form, prover likformigt från undersidan av kurvan f ( x ) utan att behöva avvisa några punkter, enligt följande:

1. ₀₀ Välj ett startvärde x för vilket f ( x ) > 0.
2. ₀ Prova ett y- värde jämnt mellan 0 och f ( x ).
3. Rita en horisontell linje över kurvan vid denna y- position.
4. Prova en punkt ( x , y ) från linjesegmenten inom kurvan.
5. Upprepa från steg 2 med det nya x -värdet.

Motivationen här är att ett sätt att sampla en punkt enhetligt inifrån en godtycklig kurva är att först rita tunna horisontella skivor med jämn höjd över hela kurvan. Sedan kan vi ta prov på en punkt i kurvan genom att slumpmässigt välja en skiva som faller vid eller under kurvan vid x-positionen från föregående iteration, och sedan slumpmässigt välja en x-position någonstans längs skivan. Genom att använda x-positionen från den tidigare iterationen av algoritmen väljer vi i det långa loppet ut skivor med sannolikheter proportionella mot längden på deras segment inom kurvan. Den svåraste delen av denna algoritm är att hitta gränserna för det horisontella segmentet, vilket innebär att invertera funktionen som beskriver fördelningen som samplas från. Detta är särskilt problematiskt för multimodala distributioner, där skivan kan bestå av flera diskontinuerliga delar. Det är ofta möjligt att använda en form av avvisningssampling för att övervinna detta, där vi provar från en större skiva som är känd för att innehålla den önskade skivan i fråga, och sedan kastar punkter utanför den önskade skivan. Denna algoritm kan användas för att sampla från området under vilken kurva som helst, oavsett om funktionen integreras till 1. Faktum är att skalning av en funktion med en konstant har ingen effekt på de samplade x-positionerna. Detta innebär att algoritmen kan användas för att sampla från en fördelning vars sannolikhetstäthetsfunktion endast är känd upp till en konstant (dvs vars normaliseringskonstant är okänd), vilket är vanligt i beräkningsstatistik .

Genomförande

Slice sampling har fått sitt namn från det första steget: definiera ett segment genom att sampla från en hjälpvariabel $Y$ . Denna variabel är samplade från $[0,f(x)]$ , där $f(x)$ är antingen sannolikhetstäthetsfunktionen (PDF) för X eller är åtminstone proportionell mot sin PDF. Detta definierar en del av X där $f(x)\geq Y$ . Med andra ord, vi tittar nu på en region av X där sannolikhetstätheten är minst $Y$ . Sedan samplas nästa värde på X likformigt från denna skiva. Ett nytt värde på $Y$ samplas, sedan X , och så vidare. Detta kan visualiseras som alternativt sampling av y-positionen och sedan x-positionen för punkter under PDF, sålunda X :en från den önskade fördelningen. Y ${\displaystyle Y} -värdena har inga speciella konsekvenser eller tolkningar utöver deras$ för proceduren.

Om både PDF-filen och dess invers är tillgängliga, och distributionen är unimodal, är det enkelt att hitta skivan och ta prov från den. Om inte, kan en utstegsprocedur användas för att hitta en region vars ändpunkter faller utanför segmentet. Sedan kan ett prov tas från skivan med hjälp av avvisningsprovtagning . Olika procedurer för detta beskrivs i detalj av Neal.

Observera att, i motsats till många tillgängliga metoder för att generera slumpmässiga tal från olikformiga distributioner, kommer slumpmässiga variationer som genereras direkt av detta tillvägagångssätt att uppvisa ett seriellt statistiskt beroende. Detta beror på att vi för att rita nästa prov definierar segmentet baserat på värdet av f ( x ) för det aktuella provet.

Jämfört med andra metoder

Skivprovtagning är en Markov-kedjemetod och tjänar som sådan samma syfte som Gibbs provtagning och Metropolis. Till skillnad från Metropolis finns det inget behov av att manuellt ställa in kandidatfunktionen eller kandidatstandardavvikelsen.

Kom ihåg att Metropolis är känslig för stegstorlek. Om stegstorleken är för liten slumpmässig gång långsam dekorrelation. Om stegstorleken är för stor är det stor ineffektivitet på grund av en hög avvisningsfrekvens.

I motsats till Metropolis justerar skivprovtagning automatiskt stegstorleken för att matcha den lokala formen på densitetsfunktionen. Implementering är utan tvekan enklare och effektivare än Gibbs sampling eller enkla Metropolis-uppdateringar.

Observera att, i motsats till många tillgängliga metoder för att generera slumpmässiga tal från olikformiga distributioner, kommer slumpmässiga variationer som genereras direkt av detta tillvägagångssätt att uppvisa ett seriellt statistiskt beroende. Med andra ord, inte alla punkter har samma oberoende sannolikhet för urval. Detta beror på att för att rita nästa prov, definierar vi segmentet baserat på värdet av f(x) för det aktuella provet. De genererade proverna är dock markoviska och förväntas därför konvergera till korrekt fördelning på lång sikt.

Slice Sampling kräver att fördelningen som ska provtas är utvärderbar. Ett sätt att lätta på detta krav är att ersätta en evaluerbar fördelning som är proportionell mot den verkliga oevaluerbara fördelningen.

Univariat fall

För ett givet prov x väljs ett värde för y från [0, f ( x )], vilket definierar en "del" av fördelningen (visas med den heldragna horisontella linjen). I det här fallet finns det två skivor åtskilda av ett område utanför distributionsområdet.

För att ta prov på en slumpvariabel X med densitet f ( x ) introducerar vi en hjälpvariabel Y och itererar enligt följande:

• Med ett urval x väljer vi y enhetligt slumpmässigt från intervallet [0, f ( x )];
• givet y väljer vi x likformigt slumpmässigt från mängden $f^{-1}[y,+\infty )$ .
• Provet av x erhålls genom att ignorera y- värdena.

Vår hjälpvariabel Y representerar en horisontell "del" av fördelningen. Resten av varje iteration ägnas åt att sampla ett x -värde från skivan som är representativt för tätheten av den region som beaktas.

I praktiken är provtagning från en horisontell del av en multimodal distribution svårt. Det finns en spänning mellan att erhålla en stor provtagningsregion och därigenom möjliggöra stora rörelser i distributionsutrymmet, och att erhålla en enklare provtagningsregion för att öka effektiviteten. Ett alternativ för att förenkla denna process är regional expansion och sammandragning.

• Först används en breddparameter w för att definiera området som innehåller det givna 'x- värdet. Varje ändpunkt i detta område testas för att se om den ligger utanför den givna skivan. Om inte, förlängs området i lämplig riktning med w tills slutet av båda ändpunkterna ligger utanför skivan.
• Ett kandidaturval väljs enhetligt från denna region. Om kandidatprovet ligger inuti skivan, accepteras det som det nya provet. Om den ligger utanför segmentet blir kandidatpunkten den nya gränsen för regionen. Ett nytt kandidatprov tas enhetligt. Processen upprepas tills kandidatprovet är inom skivan. (Se diagram för ett visuellt exempel).

Att hitta ett prov givet en uppsättning skivor (skivorna representeras här som blå linjer och motsvarar de heldragna linjerna i föregående graf av f ( x ) ). a) En breddparameter w ställs in. b) Ett område med bredd w identifieras runt en given punkt $x_{0}$ . c) Regionen utökas med w tills båda ändpunkterna är utanför den övervägda delen. d) $x_{1}$ väljs enhetligt från regionen. e) Eftersom $x_{1}$ ligger utanför den aktuella delen, justeras regionens vänstra gräns till $x_{1}$ . f) Ett annat enhetligt prov $x$ tas och accepteras som provet eftersom det ligger inom den övervägda delen.

→

Slice-in-Gibbs provtagning

I en Gibbs-sampler måste man dra effektivt från alla fullständiga villkorsfördelningar. När sampling från en fullständig densitet inte är lätt, kan en enda iteration av skivsampling eller Metropolis-Hastings-algoritmen användas inom-Gibbs för att sampla från variabeln i fråga. Om den fullständiga densiteten är log-konkav, är ett effektivare alternativ tillämpningen av adaptiva rejection sampling (ARS) metoder. När ARS-teknikerna inte kan tillämpas (eftersom det fullständiga villkoret är icke-log-konkavt), används ofta de adaptiva avvisningsalgoritmerna för Metropolis-sampling .

Multivariata metoder

Behandla varje variabel oberoende

Enstaka variabel skivsampling kan användas i multivariatfallet genom att sampla varje variabel i tur och ordning upprepade gånger, som i Gibbs sampling. För att göra det krävs att vi för varje komponent ${\displaystyle x_{i}} kan beräkna$ en funktion som är proportionell mot $p(x_{i}| x_{0}...x_{n})$ .

För att förhindra slumpmässigt gångbeteende kan överavslappningsmetoder användas för att uppdatera varje variabel i tur och ordning. Överrelaxation väljer ett nytt värde på motsatt sida av läget från det aktuella värdet, i motsats till att välja ett nytt oberoende värde från distributionen som gjort i Gibbs.

Provtagning av hyperrektangelskivor

Denna metod anpassar den univariata algoritmen till det multivariata fallet genom att ersätta den endimensionella w- regionen som används i originalet med en hyperrektangel. Hyperrektangeln H initieras till en slumpmässig position över skivan. H krymps sedan när poäng från den förkastas.

Reflekterande skivprovtagning

Reflekterande skivsampling är en teknik för att undertrycka slumpmässigt gångbeteende där de successiva kandidatproverna av fördelningen f ( x ) hålls inom gränserna för skivan genom att "reflektera" riktningen för provtagningen inåt mot skivan när gränsen väl har träffats.

I denna grafiska representation av reflekterande provtagning indikerar formen gränserna för en provtagningsskiva. Prickarna indikerar start- och stopppunkter för en provtagningspromenad. När proverna träffar gränsen för skivan, "reflekteras" riktningen för provtagningen tillbaka in i skivan.

Exempel

Betrakta ett enstaka variabelt exempel. Anta att vår sanna fördelning är en normalfördelning med medelvärde 0 och standardavvikelse 3, $g(x)\sim N(0,3^{2})$ . Så: $f(x)={\frac {1}{\sqrt {2\pi \cdot 3^{ 2}}}}\ e^{-{\frac {(x-0)^{2}}{2\cdot 3^{2}}}}$ . Toppen av fördelningen är uppenbarligen vid $x=0$ , vid vilken punkt $f(x)\approx 0,1330$ .

1. Vi drar först ett enhetligt slumpmässigt värde y från intervallet f ( x ) för att definiera våra skivor. f ( x ) sträcker sig från 0 till ~0,1330, så alla värden mellan dessa två ytterligheter räcker. Antag att vi tar y = 0,1. Problemet blir hur man samplar punkter som har värden y > 0,1.
2. Därefter ställer vi in ​​vår breddparameter w som vi kommer att använda för att utöka vår övervägande region. Detta värde är godtyckligt. Antag att w = 2.
3. Därefter behöver vi ett initialt värde för x . Vi drar x från den enhetliga fördelningen inom domänen av f ( x ) som uppfyller f ( x ) > 0,1 (vår y -parameter). Antag att x = 2. Detta fungerar eftersom f (2) = ~0,1065 > 0,1.
4. Eftersom x = 2 och w = 2, begränsas vår aktuella region av intresse av (1, 3).
5. Nu testas varje ändpunkt för detta område för att se om den ligger utanför den givna skivan. Vår högra gräns ligger utanför vår skiva ( f (3) = ~0,0807 < 0,1), men det vänstra värdet gör det inte ( f (1) = ~0,1258 > 0,1). Vi expanderar den vänstra gränsen genom att lägga w tills den sträcker sig förbi gränsen för skivan. Efter denna process är de nya gränserna för vår intresseregion (−3, 3).
6. Därefter tar vi ett enhetligt prov inom (−3, 3). Antag att detta prov ger x = −2,9. Även om detta prov är inom vår region av intresse, ligger det inte inom vår del (f(2,9) = ~0,08334 < 0,1), så vi ändrar den vänstra gränsen för vår region av intresse till denna punkt. Nu tar vi ett enhetligt prov från (−2,9, 3). Anta att vårt prov den här gången ger x = 1, vilket är inom vår skiva, och därmed är det accepterade urvalet genom skivsampling. Hade vårt nya x inte varit inom vårt segment skulle vi fortsätta krympning/omsamplingsprocessen tills ett giltigt x inom gränserna hittas.

Om vi ​​är intresserade av fördelningens topp kan vi fortsätta att upprepa denna process eftersom den nya punkten motsvarar en högre f ( x ) än den ursprungliga punkten.

Ett annat exempel

För att sampla från normalfördelningen $N(0,1)$ väljer vi först ett initialt x — säg 0. Efter varje urval av x väljer vi y likformigt slumpmässigt från ${\displaystyle (0,e^{-x^{2}/2}/{\sqrt {2\pi }}]} , som avgränsar pdf-filen$ för $N(0,1)$ Efter varje y- prov väljer vi x likformigt slumpmässigt från $[-\alpha ,\alpha ]$ där ${ \displaystyle \alpha ={\sqrt {-2\ln(y{\sqrt {2\pi }})}}} .$ Detta är segmentet där $f(x)>y$ .

En implementering i Macsyma -språket är:

  
      
       
   skiva  (  x  )  :=  block  ([  y  ,  alfa  ]  ,  y:  slumpmässig  (  exp  (  -  x  ^  2  /  2.0  )  /  sqrt  (  2.0  *  dfloat  (  %  pi  )))  ,  alfa:  sqrt  (  -2.0  *  ln  (  y)  *  sqrt  (  2,0  *  dfloat  (  %  pi  ))))  ,  x:  signum  (  slumpmässigt  ())  *  slumpmässigt  (  alfa  ) )  ; 

Se även

• Markov-kedjan Monte Carlo

externa länkar

• http://www.probability.ca/jeff/java/slice.html