Post-Turing maskin

En Post –Turing - maskin är en "programformulering" av en typ av Turing-maskin , som består av en variant av Emil Posts Turing -ekvivalenta beräkningsmodell . Posts modell och Turings modell, även om de var väldigt lika varandra, utvecklades oberoende av varandra. Turings tidning mottogs för publicering i maj 1936, följt av Posts i oktober. En Post-Turing-maskin använder ett binärt alfabet , en oändlig sekvens av binära lagringsplatser och ett primitivt programmeringsspråk med instruktioner för dubbelriktad rörelse mellan lagringsplatserna och ändring av deras innehåll en i taget. Namnen "Post–Turing program" och "Post–Turing machine" användes av Martin Davis 1973–1974 (Davis 1973, s. 69ff). Senare 1980 använde Davis namnet "Turing–Post-programmet" (Davis, i Steen s. 241).

1936: Stolpemodell

I sin artikel "Finite Combinatory Processes—Formulation 1" från 1936 beskrev Emil Post en modell som han antog är " logiskt likvärdig med rekursivitet ".

Posts modell av en beräkning skiljer sig från Turing-maskinmodellen i en ytterligare "atomisering" av de handlingar som en mänsklig "dator" skulle utföra under en beräkning.

Posts modell använder ett " symbolutrymme " som består av en "tvåvägs oändlig sekvens av mellanslag eller rutor", varje ruta kan vara i något av två möjliga tillstånd, nämligen "markerad" (som genom ett enda vertikalt slag) och "omärkt " (tom). Inledningsvis, ändligt - många av rutorna är markerade, resten är omarkerade. En "arbetare" är då att röra sig bland lådorna, vara i och endast arbeta i en ruta åt gången, enligt en fast ändlig "uppsättning av anvisningar" ( instruktioner ), som är numrerade i ordning (1,2,3, ..., n ). Med utgångspunkt från en ruta "utpekad som utgångspunkt" ska arbetaren följa instruktionerna en i taget, med början på instruktion 1.

Det finns fem olika primitiva operationer som arbetaren kan utföra:

(a) Markera rutan den är i, om den är tom

(b) Radera markeringen i rutan den är i, om den är markerad (

c) Flytta till rutan till höger

(d) Flytta till rutan på dess vänster

(e) Avgöra om rutan den är i, är eller inte är markerad.

Sedan ska den i: ^te "riktningen" (instruktionen) som ges till arbetaren vara en av följande former:

Utför operation O _i [ O _i = (a), (b), (c) eller (d)] och följ sedan riktningen j _i
Utför operation (e) och beroende på om svaret är ja eller nej, följ riktningen j _i ' eller j _i ' på motsvarande sätt
Sluta .

(Ovanstående indragna text och kursiv stil är som i originalet.) Post anmärker att denna formulering är "i dess inledande stadier" av utveckling, och nämner flera möjligheter till "större flexibilitet" i sin slutliga "definitiva form", bl.a.

att ersätta oändligheten av rutor med ett ändligt utdragbart symbolutrymme, "förlänga de primitiva operationerna för att möjliggöra den nödvändiga förlängningen av det givna finita symbolutrymmet allt eftersom processen fortskrider",
använda ett alfabet med fler än två symboler, "har mer än ett sätt att markera en ruta",
introducerar ändligt många "fysiska objekt för att fungera som pekare, som arbetaren kan identifiera och flytta från ruta till ruta".

1947: Posts formella minskning av Turing 5-tuplar till 4-tuplar

Som kort nämnts i artikeln Turing machine , Post, i sin uppsats från 1947 ( Recursive Unsolvability of a Problem of Thue ) finfördelade Turing 5-tuplar till 4-tuplar:

"Våra fyrlingar är femlingar i Turing-utvecklingen. Det vill säga när vår standardinstruktion beställer antingen en utskrift (övertryck) eller rörelse, vänster eller höger, beställer Turings standardinstruktion alltid en utskrift och en rörelse, höger, vänster eller ingen" ( fotnot 12, Undecidable , s. 300)

Liksom Turing definierade han radering som att skriva ut en symbol "S0". Och så hans modell medgav fyrlingar av endast tre typer (jfr. Undecidable , s. 294):

q _i S _j L q _l ,

q _i S _j R q _l ,

q _i S _j S _k q _l

Vid denna tidpunkt behöll han fortfarande Turing-statsmaskinkonventionen – han hade inte formaliserat uppfattningen om en antagen sekventiell exekvering av steg förrän ett specifikt test av en symbol "förgrenade" utförandet någon annanstans.

1954, 1957: Wang modell

För en ytterligare minskning – till endast fyra instruktioner – av Wang-modellen som presenteras här, se Wang B-maskin .

Wang (1957, men presenterad för ACM 1954) citeras ofta (jfr Minsky (1967), s. 200) som källan till "programformuleringen" av Turing-maskiner med binära band som använder numrerade instruktioner från uppsättningen

skriv 0

skriv 1

flytta vänster

flytta höger

om skannar 0 sedan gå till instruktion i

om skannar 1 så gå till instruktion j

Vilken Turing-maskin som helst med binärt band konverteras lätt till ett motsvarande "Wang-program" med hjälp av instruktionerna ovan.

1974: första Davis-modellen

Martin Davis var en student på Emil Post. Tillsammans med Stephen Kleene avslutade han sin Ph.D. under Alonzo Church (Davis (2000) 1:a och 2:a fotnoten s. 188).

Följande modell presenterade han i en serie föreläsningar för Courant Institute vid NYU 1973–1974. Detta är modellen som Davis formellt tillämpade namnet "Post–Turing-maskin" på med dess "Post–Turing-språk". Instruktionerna antas utföras sekventiellt (Davis 1974, s. 71):

1978: andra Davis-modellen

Följande modell visas som en uppsats Vad är en beräkning? i Steen sidorna 241–267. Av någon anledning har Davis döpt om sin modell till en "Turing–Post-maskin" (med en bakåtskjutande på sidan 256.)

I följande modell tilldelar Davis siffrorna "1" till Posts "markering/snedstreck" och "0" till den tomma rutan. För att citera Davis: "Vi är nu redo att introducera programmeringsspråket Turing–Post. På detta språk finns det sju typer av instruktioner:

"UTSKRIFT 1

"PRINT 0

"GÅ HÖGER

"GÅ VÄNSTER

"GÅ TILL STEG i OM 1 SKANNAS

0 "GÅ TILL STEG i OM SKANNAS

"STOPPA

"Ett Turing–Post-program är då en lista med instruktioner, som var och en är av ett av dessa sju slag. Naturligtvis, i ett faktiskt program måste bokstaven i i ett steg av antingen den femte eller sjätte typen ersättas med en bestämt (positivt heltal)." (Davis i Steen, s. 247).

1994 (2:a upplagan): Davis–Sigal–Weyukers Post–Turing-programmodell

"Även om formuleringen av Turing som vi har presenterat ligger närmare den som Emil Post ursprungligen gav, var det Turings analys av beräkningen som har fått denna formulering att verka så pass passande. Detta språk har spelat en grundläggande roll i teoretisk datavetenskap." (Davis et al. (1994) s. 129)

₀ Denna modell gör det möjligt att skriva ut flera symboler. Modellen tillåter B (blank) istället för S . Tejpen är oändlig i båda riktningarna. Antingen rör sig huvudet eller bandet, men deras definitioner av HÖGER och VÄNSTER anger alltid samma resultat i båda fallen (Turing använde samma konvention).

SKRIV UT σ ;Ersätt den skannade symbolen med σ

OM σ GOTO L ;OM den skannade symbolen är σ GÅ DÅ till "den första" instruktionen märkt L

HÖGER ;Skanna kvadraten omedelbart till höger om den ruta som för närvarande skannas till

VÄNSTER ;Skanna kvadraten omedelbart till vänster om den ruta som för närvarande skannas

Denna modell reducerar till de binära { 0, 1 }-versionerna som presenteras ovan, som visas här:

SKRIV UT 0 = RADERA ;Ersätt skannad symbol med 0 = B = BLANK

UTSKRIVNING 1 ;Ersätt skannad symbol med 1

OM 0 GÅ TILL L ;OM skannade symbol är 0 GÅ DÅ till "den första" instruktionen märkt L

OM 1 GÅT L ;OM skannad symbol är 1 GÅ DÅ till "den första" instruktionen märkt L

HÖGER ;Skanna ruta omedelbart till höger om den ruta som för närvarande skannas

VÄNSTER ;Skanna ruta omedelbart till vänster om den ruta som för närvarande skannas

Exempel på Post–Turing-maskinen

Atomizing Turing-kvintuplar till en sekvens av Post-Turing-instruktioner

Följande "reduktion" (sönderdelning, finfördelning) metod – från 2-symbol Turing 5-tupler till en sekvens av 2-symbol Post-Turing instruktioner – finns i Minsky (1961). Han konstaterar att denna minskning till "ett program ... en sekvens av instruktioner " är i andan av Hao Wangs B-maskin (kursiv stil i original, jfr Minsky (1961) s. 439).

(Minskys reduktion till vad han kallar "en sub-rutin" resulterar i 5 snarare än 7 Post-Turing-instruktioner. Han finförde inte Wi0: "Skriv symbol Si0; gå till nytt tillstånd Mi0", och Wi1: "Skriv symbol Si1; gå till nytt tillstånd Mi1". Följande metod finfördelar Wi0 och Wi1 ytterligare; i alla andra avseenden är metoderna identiska.)

Denna minskning av Turing 5-tupler till Post-Turing-instruktioner kanske inte resulterar i ett "effektivt" Post-Turing-program, men det kommer att vara troget det ursprungliga Turing-programmet.

I följande exempel omvandlas varje Turing 5-tuppel av 2-tillståndsupptagen bävern till

ett initialt villkorligt "hopp" (goto, gren), följt av
2 bandinstruktioner för "0"-fallet – Skriv ut eller Radera eller Ingen, följt av Vänster eller Höger eller Ingen, följt av
ett ovillkorligt "hopp" för "0"-fallet till nästa instruktion
2 bandinstruktioner för "1"-fodralet – Skriv ut eller Radera eller Ingen, följt av Vänster eller Höger eller Ingen, följt av
ett ovillkorligt "hopp" för "1"-fallet till dess nästa instruktion

för totalt 1 + 2 + 1 + 2 + 1 = 7 instruktioner per Turing-tillstånd.

Till exempel är 2-tillståndsupptagen bäverns "A" Turing-tillstånd, skrivet som två rader med 5-tuplar:

Initial m-konfiguration (turingtillstånd)	Tejpsymbol	Utskriftsoperation	Tejprörelse	Slutlig m-konfiguration (turingtillstånd)
A	0	P	R	B
A	1	P	L	B

Tabellen representerar bara en enda Turing-"instruktion", men vi ser att den består av två rader med 5-tupler, en för fallet "bandsymbol under huvudet = 1", den andra för fallet "bandsymbol under huvudet = 0 ". Turing observerade ( Undecidable , s. 119) att de två vänstra kolumnerna – "m-konfiguration" och "symbol" – representerar maskinens nuvarande "konfiguration" – dess tillstånd inklusive både Tape och Table vid det ögonblicket – och de tre sista kolumnerna är dess efterföljande "beteende". Eftersom maskinen inte kan vara i två "tillstånd" samtidigt, måste maskinen "förgrena sig" till antingen den ena eller den andra konfigurationen:

Initial m-konfiguration och symbol S	Utskriftsoperation	Tejprörelse	Slutlig m-konfiguration
S=0 →	P →	R →	B
→ A <
S=1 →	P →	L →	B

Efter "konfigurationsgrenen" (J1 xxx) eller (J0 xxx) följer maskinen ett av de två efterföljande "beteendena". Vi listar dessa två beteenden på en rad och numrerar (eller märker) dem sekventiellt (unikt). Under varje hopp (gren, gå till) placerar vi dess hopp till "nummer" (adress, plats):

	Initial m-konfiguration & symbol S	Utskriftsoperation	Tejprörelse	Slutligt m-konfigurationsfall S=0	Utskriftsoperation	Tejprörelse	Slutligt m-konfigurationsfall S=1
	Om S=0 då:	P	R	B
	→ A <
	Om S=1 då:				P	L	B
instruktion #	1	2	3	4	5	6	7
Post-Turing instruktion	J1	P	R	J	P	L	J
hoppa till instruktion #	5			B			B

Enligt Post-Turing-maskinens konventioner består var och en av instruktionerna för utskrift, radering, vänster och höger av två åtgärder:

Bandåtgärd: {P, E, L, R}, sedan
Tabellåtgärd: gå till nästa instruktion i följd

Och enligt Post–Turing-maskinens konventioner består de villkorliga "hoppen" J0xxx, J1xxx av två åtgärder:

Tape action: titta på symbolen på tejpen under huvudet
Tabellåtgärd: Om symbolen är 0 (1) och J0 (J1), gå till xxx annars gå till nästa instruktion i följd

Och enligt Post–Turing-maskinens konventioner består det ovillkorliga "hoppet" Jxxx av en enda åtgärd, eller om vi vill reglera sekvensen med 2 åtgärder:

Tape action: titta på symbolen på tejpen under huvudet
Tabellåtgärd: Om symbolen är 0, gå till xxx annars om symbolen är 1, gå till xxx.

Vilka och hur många hopp behövs? Det ovillkorliga hoppet J xxx är helt enkelt J0 följt omedelbart av J1 (eller vice versa). Wang (1957) visar också att endast ett villkorligt hopp krävs, dvs antingen J0 xxx eller J1 xxx. Men med denna begränsning blir maskinen svår att skriva instruktioner för. Ofta används bara två, dvs

{ J0 xxx, J1 xxx }
{ J1 xxx, J xxx }
{ J0 xxx, J xxx },

men användningen av alla tre { J0 xxx, J1 xxx, J xxx } eliminerar extra instruktioner. I exemplet med 2-tillstånd Busy Beaver använder vi bara { J1 xxx, J xxx }.

2-stats upptagen bäver

Uppdraget för den upptagna bävern är att skriva ut så många som möjligt innan han stannar. "Skriv ut"-instruktionen skriver en 1, "Radera"-instruktionen (används inte i detta exempel) skriver en 0 (dvs. den är samma som P0). Bandet rör sig "vänster" eller "höger" (dvs. "huvudet" är stillastående).

Statustabell för en 2-tillstånd Turing-maskin upptagen bäver :

Tejpsymbol	Skriv symbol	Flytta bandet	Nästa stat	Skriv symbol	Flytta bandet	Nästa stat
Tejpsymbol	Nuvarande tillstånd A			Nuvarande tillstånd B
0	1	R	B	1	L	A
1	1	L	B	1	N	H

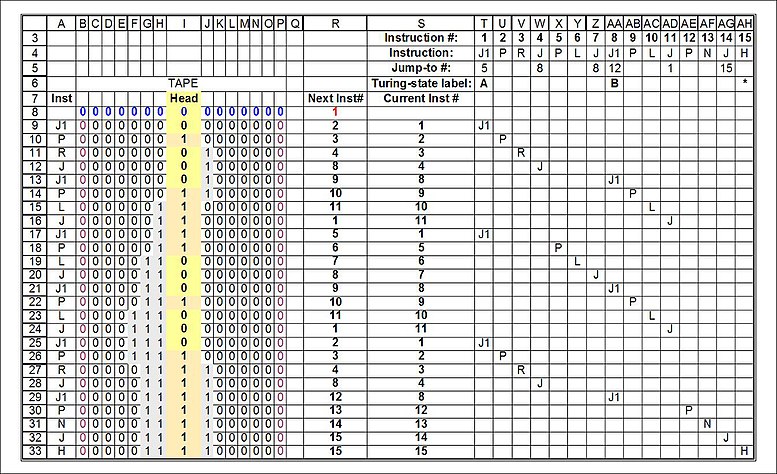
Instruktioner för Post-Turing-versionen av en upptagen bäver med 2 tillstånd: observera att alla instruktioner är på samma rad och i sekvens. Detta är en betydande avvikelse från "Turing"-versionen och är i samma format som vad som kallas ett "datorprogram":

Instruktion #	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Instruktion	J1	P	R	J	P	L	J	J1	P	L	J	P	N	J	H
Hoppa till #	5			8			8	12			1			15
Turing-state-etikett	A							B							H

Alternativt kan vi skriva tabellen som en sträng. Användningen av "parameterseparatorer" ":" och instruktionsseparatorer "," är helt vårt val och visas inte i modellen. Det finns inga konventioner (men se Booth (1967) s. 374, och Boolos och Jeffrey (1974, 1999) s. 23), för några användbara idéer om hur man kombinerar tillståndsdiagramkonventioner med instruktionerna – dvs. att använda pilar för att indikera destinationen för hoppen). I exemplet omedelbart nedan är instruktionerna sekventiella med början från "1", och parametrarna/"operander" anses vara en del av deras instruktioner/"opkoder":

J1:5, P, R, J:8, P, L, J:8, J1:12, P, L, J1:1, P, N, J:15, H

Tillståndsdiagrammet för en upptagen bäver med två tillstånd (liten ritning, högra hörnet) konverteras till motsvarande Post–Turing-maskin med ersättning av 7 Post–Turing-instruktioner per "Turing"-tillstånd.

HALT-instruktionen lägger till det 15:e tillståndet.

En "körning" av den 2-tillståndsupptagna bävern med alla mellansteg i Post–Turing-maskinen visade.

Anteckningar

Stephen C. Kleene , Introduction to Meta-Mathematics, North-Holland Publishing Company , New York, 10:e upplagan 1991, publicerad första gången 1952. Kapitel XIII är en utmärkt beskrivning av Turing-maskiner; Kleene använder en postliknande modell i sin beskrivning och medger att Turing-modellen kan finfördelas ytterligare, se fotnot 1.
Martin Davis , redaktör: The Undecidable, Basic Papers on Undecidable Propositions, Unsolvable Problems and Computable Functions, Raven Press, New York, 1965. Paper inkluderar de av Gödel , Church , Rosser , Kleene och Post.
Martin Davis , "What is a computation", i Mathematics Today , Lynn Arthur Steen, Vintage Books (Random House), 1980. Ett underbart litet papper, kanske det bästa som någonsin skrivits om Turing Machines. Davis reducerar Turing Machine till en mycket enklare modell baserad på Posts modell av en beräkning. Innehåller en liten biografi om Emil Post.
Martin Davis , Computability: with Notes av Barry Jacobs , Courant Institute of Mathematical Sciences, New York University, 1974.
Martin Davis , Ron Sigal, Elaine J. Weyuker , (1994) Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science – 2nd edition , Academic Press: Harcourt, Brace & Company, San Diego, 1994 ISBN 0-12-206382- 1 (Första upplagan, 1983).
Fred Hennie, Introduction to Computability , Addison–Wesley, 1977.
Marvin Minsky , (1961), Recursive Unsolvability of Posts problem med "Tag" och andra ämnen i teorin om Turing Machines, Annals of Mathematics, Vol. 74, nr 3, november 1961.
Roger Penrose , The Emperor's New Mind: Concerning computers, Minds and the Laws of Physics , Oxford University Press, Oxford England, 1990 (med korrigeringar). Jfr. Kapitel 2, "Algorithms and Turing Machines". En överkomplicerad presentation (se Davis uppsats för en bättre modell), men en grundlig presentation av Turing-maskiner och stoppproblemet och Churchs lambdakalkyl .
Hao Wang (1957): "En variant av Turings teori om datormaskiner", Journal of the Association for Computing Machinery (JACM) 4, 63–92.