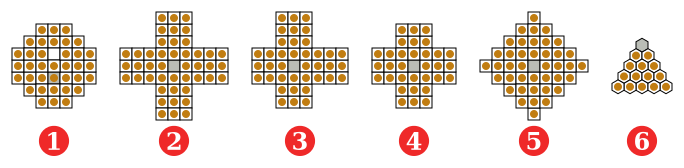
Peg solitaire

Prinsessan av Soubise spelar patiens, 1697

Peg solitaire , Solo Noble eller helt enkelt Solitaire är ett brädspel för en spelare som involverar förflyttning av pinnar på en bräda med hål. Vissa uppsättningar använder kulor i en bräda med fördjupningar. Spelet är känt som solitaire i Storbritannien och som peg solitaire i USA där "patiens" nu är det vanliga namnet för tålamod . Det kallas också Brainvita i Indien , där set säljs kommersiellt under detta namn.

Ludvig XIV: s hov och det specifika datumet 1697, med en gravyr gjord tio år senare av Claude Auguste Berey av Anne de Rohan-Chabot, prinsessan av Soubise, med pusslet av hennes sida. Augustiupplagan 1697 av den franska litterära tidskriften Mercure galant innehåller en beskrivning av styrelsen, regler och exempelproblem. Detta är den första kända referensen till spelet i tryck.

Standardspelet fyller hela brädet med pinnar förutom det centrala hålet. Målet är att göra giltiga drag, att tömma hela brädet förutom en ensam pinne i det centrala hålet.

Styrelse

Engelsk patiensbräda
Europeisk peg-patiensbräda

Det finns två traditionella brädor ('.' som en första pinne, 'o' som ett initialt hål):

engelsk Europeiska 
· · · · · · · · · · · · · · · o · · · · · · · · · · · · · ·
 
· · · · · · · · · · · · · · · · · o · · · · · · · · · · · · · · · ·

Spela

Spelar Peg Solitaire
En man som spelar triangulär patiens på en Cracker Barrel- restaurang.

Ett giltigt drag är att hoppa en pinne ortogonalt över en intilliggande pinne i ett hål två positioner bort och sedan ta bort den hoppade pinnen.

I diagrammen som följer anger · en tapp i ett hål, * med fet stil anger stiftet som ska flyttas och o anger ett tomt hål. Ett blått ¤ är hålet som den aktuella tappen flyttade från; en röd * är den slutliga positionen för den pinnen, ett rött o är hålet på den pinnen som hoppades och togs bort.

Sålunda är giltiga drag i var och en av de fyra ortogonala riktningarna:

     *  · o →  ¤  o  *  Hoppa till höger 

     o ·  *  →  *  o  ¤  Hoppa till vänster 

        *  ¤  · →  o  Hoppa ner  o  * 

  
      o  *  · →  o  Hoppa upp  *  ¤

På en engelsk bräda kan de tre första dragen vara:

   · · · · · · · · · · · · ·  *  · ·  ¤  · · o · ·  *  · · · · · · · · · ·  o  · · · ·  ¤  o  *  · · · · oo  o  · · · · · · o · · · · · ·  *  · · · · · · · · · · ·  ¤  · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Strategi

Det finns många olika lösningar på standardproblemet, och en notation som används för att beskriva dem tilldelar bokstäver till hålen (även om siffror också kan användas):

Engelska Europeiska abcabc defydefz ghijklmghijklm nopx PON nopx PON MLKJIHGMLKJIHG FEDZFEDY CBACBA

Denna spegelbildsnotation används bland annat eftersom en uppsättning alternativa spel på den europeiska brädet är att börja med ett hål vid någon position och att sluta med en enda pinne i dess spegelvända position. På den engelska brädan är motsvarande alternativa spel att börja med ett hål och sluta med en pinne på samma position.

Det finns ingen lösning på den europeiska brädet med det initiala hålet centralt, om bara ortogonala rörelser är tillåtna. Detta kan lätt ses på följande sätt, genom ett argument från Hans Zantema . Dela upp brädans positioner i A-, B- och C-positioner enligt följande: 

ABC ABCAB ABCABCA BCABCAB CABCABC BCABC ABC

Inledningsvis med endast den centrala positionen ledig är antalet täckta A-positioner 12, antalet täckta B-positioner är 12 och även antalet täckta C-positioner är 12. Efter varje drag ökar eller minskar antalet täckta A-positioner med en, och samma för antalet täckta B-positioner och antalet täckta C-positioner. Efter ett jämnt antal drag är därför alla dessa tre nummer jämna, och efter ett udda antal drag är alla dessa tre nummer udda. Därför kan en slutlig position med endast en peg inte nås, eftersom det skulle kräva att ett av dessa nummer är ett (positionen för peg, en är udda), medan de andra två talen är noll, därav jämna.

Det finns emellertid flera andra konfigurationer där ett enda initialt hål kan reduceras till en enda tapp.

En taktik som kan användas är att dela upp brädan i paket om tre och att rensa (ta bort) dem helt med hjälp av en extra pinne, katalysatorn, som hoppar ut och sedan hoppar tillbaka igen . I exemplet nedan * katalysatorn.: 

     *  · o  ¤  o  *  o  *  ·  *  o  ¤  · → · →  o  → o · ·  ¤  o

Denna teknik kan användas med en linje av 3, ett block av 2·3 och en 6-pin L-form med en bas av längd 3 och upprätt av längd 4.

Andra alternativa spel inkluderar att börja med två tomma hål och avsluta med två pinnar i dessa hål. Börjar också med ett hål här och slutar med en pinne där . På en engelsk bräda kan hålet vara var som helst och den sista pinnen kan bara hamna där multipler av tre tillåter. Således kan ett hål vid a bara lämna en enda tapp vid a , p , O eller C .

Studier om pinnepatiens

En grundlig analys av spelet är känd. Denna analys introducerade ett begrepp som kallas pagodfunktion som är ett starkt verktyg för att visa omöjligheten av ett givet, generaliserat, peg solitaire-problem.

En lösning för att hitta en pagodfunktion, som visar omöjligheten av ett givet problem, är formulerad som ett linjärt programmeringsproblem och lösbart i polynomtid.

En uppsats 1990 behandlade de generaliserade Hi-Q-problemen som är likvärdiga med peg-patiensproblemen och visade deras NP-fullständighet .

I ett papper från 1996 formulerades ett problem med pinnpatiens som ett kombinatoriskt optimeringsproblem och diskuterade egenskaperna hos den möjliga region som kallas "en solitärkon".

1999 löstes peg solitaire helt på en dator med en uttömmande sökning genom alla möjliga varianter. Det uppnåddes genom att använda symmetrierna, effektiv lagring av brädkonstellationer och hashing.

År 2001 utvecklades en effektiv metod för att lösa problem med pinnpatiens.

En opublicerad studie från 1989 om en generaliserad version av spelet på den engelska brädet visade att varje möjligt problem i det generaliserade spelet har 2 9 möjliga distinkta lösningar, exklusive symmetrier, eftersom den engelska brädet innehåller 9 distinkta 3×3 delrutor. En konsekvens av denna analys är att sätta en nedre gräns för storleken på eventuella problem med "inverterad position", där de celler som initialt ockuperades lämnas tomma och vice versa. Varje lösning på ett sådant problem måste innehålla minst 11 drag, oavsett de exakta detaljerna i problemet.

Det kan bevisas med hjälp av abstrakt algebra att det bara finns 5 fasta brädpositioner där spelet framgångsrikt kan avslutas med en pinne.

Lösningar till det engelska spelet

Interaktiv lösningsguide för engelska Peg Solitaire.

Den kortaste lösningen på det vanliga engelska spelet involverar 18 drag, och räknar flera hopp som enstaka drag:

Denna lösning hittades 1912 av Ernest Bergholt och visade sig vara den kortaste möjliga av John Beasley 1964.

Denna lösning kan också ses på en sida som också introducerar Wolstenholme-notationen , som är utformad för att göra det lättare att memorera lösningen.

Andra lösningar inkluderar följande lista. I dessa är notationen som används

  • Lista över starthål
  • Kolon
  • Lista över ändmålspinnar
  • Lika tecken
  • Källpinne och destinationshål (tapparna som hoppats över lämnas som en övning för läsaren)
  • , eller / ( ett snedstreck används för att separera "bitar" som en sex-purge out ) 
x:x=ex,lj,ck,Pf,DP,GI,JH,mG,GI,ik,gi,LJ,JH,Hl,lj,jh,CK,pF,AC,CK,Mg,gi,ac, ck,kI,dp,pF,FD,DP,Pp,ox x:x=ex,lj,xe/hj,Ki,jh/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp ,MK,pF/CK,DF,AC,JL,CK,LJ/PD,GI,mG,JH,GI,DP/Ox j:j=lj,Ik,jl/hj,Ki,jh/mk,Gm, Hl,fP,mk,Pf/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/Jj i:i=ki ,Jj,ik/lj,Ik,jl/AI,FD,CA,HJ,AI,JH/mk,Hl,Gm,fP,mk,Pf/ai,ca,fd,hj,ai,jh/gi,Mg ,Lh,pd,gi,dp/Ki e:e=xe/lj,Ik,jl/ck,ac,df,lj,ck,jl/GI,lH,mG,DP,GI,PD/AI,FD, CA,JH,AI,HJ/pF,MK,gM,JL,MK,Fp/hj,ox,xe d:d=fd,xe,df/lj,ck,ac,Pf,ck,jl/DP,KI ,PD/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/MK,gM,hL,pF,MK,Fp/pd b:b=jb,lj/ck, ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp,ox/xe/AI/BJ,JH, Hl,lj,jb b:x=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp /xo,dp,ox/xe/AI/BJ,JH,Hl,lj,ex a:a=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI, lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/dp,gi,pd,Mg,Lh,gi/ia a:p=ca,jb,ac/lj,ck,jl /Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/dp,gi,pd,Mg,Lh,gi/dp

Brute force attack på standard engelsk peg solitaire

Det enda ställe det är möjligt att hamna med en ensam pinne är mitten, eller mitten av en av kanterna; på det sista hoppet kommer det alltid att finnas ett alternativ att välja om man vill sluta i mitten eller kanten.

Följande är en tabell över antalet ( möjliga fältpositioner ) av möjliga brädpositioner efter n hopp , och möjligheten att samma pinne flyttas för att göra ett ytterligare hopp ( inga fler hopp ) . Intressant att notera är att det kortaste sättet att misslyckas i spelet är i sex drag, och lösningen (förutom dess rotationer och reflektioner) är unik. Ett exempel på detta är följande: 4 → 16; 23 → 9; 14 > 16; 17 > 15; 19 > 17; 31 → 23. (I den här notationen är pinnarna numrerade från vänster till höger, med början på 0, och flyttas ner för varje rad och längst till vänster när varje rad är markerad.)

OBS: Om en styrelseposition kan roteras och/eller vändas till en annan styrelseposition, räknas styrelsepositionerna som identiska.

Eftersom det bara kan bli 31 hopp kan moderna datorer enkelt undersöka alla spelpositioner inom rimlig tid.

Ovanstående sekvens "PBP" har skrivits in som A112737 i OEIS . Observera att det totala antalet nåbara styrelsepositioner (summan av sekvensen) är 23 475 688, medan det totala antalet möjliga styrelsepositioner är 8 589 934 590 (33bit-1) (2^33), så endast cirka 2,2 % av alla möjliga styrelsepositioner kan nås från och med att centrum är ledigt.

Det är också möjligt att generera alla styrelseposter. Resultaten nedan har erhållits med hjälp av verktygsuppsättningen mcrl2 (se exemplet peg_solitaire i distributionen).

I resultaten nedan har den genererat alla styrelsepositioner den verkligen nådde med början med mitten ledigt och slutat i det centrala hålet.

Lösningar på det europeiska spelet

Det finns 3 initiala icke-kongruenta positioner som har lösningar. Dessa är:

1)

0 1 2 3 4 5 6 0 o · · 1 · · · · · 2 · · · · · · 3 · · · · · · · 4 · · · · · · · 5 · ·

Möjlig lösning: [2:2-0:2, 2:0-2:2, 1:4-1:2, 3:4-1:4, 3:2-3:4, 2:3-2: 1, 5:3-3:3, 3:0-3:2, 5:1-3:1, 4:5-4:3, 5:5-5:3, 0:4-2:4, 2:1-4:1, 2:4-4:4, 5:2-5:4, 3:6-3:4, 1:1-1:3, 2:6-2:4, 0: 3-2:3, 3:2-5:2, 3:4-3:2, 6:2-4:2, 3:2-5:2, 4:0-4:2, 4:3- 4:1, 6:4-6:2, 6:2-4:2, 4:1-4:3, 4:3-4:5, 4:6-4:4, 5:4-3: 4, 3:4-1:4, 1:5-1:3, 2:3-0:3, 0:2-0:4]

2)

0 1 2 3 4 5 6 0 · · · 1 · · o · · 2 · · · · · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·

Möjlig lösning: [1:1-1:3, 3:2-1:2, 3:4-3:2, 1:4-3:4, 5:3-3:3, 4:1-4: 3, 2:1-4:1, 2:6-2:4, 4:4-4:2, 3:4-1:4, 3:2-3:4, 5:1-3:1, 4:6-2:6, 3:0-3:2, 4:5-2:5, 0:2-2:2, 2:6-2:4, 6:4-4:4, 3: 4-5:4, 2:3-2:1, 2:0-2:2, 1:4-3:4, 5:5-5:3, 6:3-4:3, 4:3- 4:1, 6:2-4:2, 3:2-5:2, 4:0-4:2, 5:2-3:2, 3:2-1:2, 1:2-1: 4, 0:4-2:4, 3:4-1:4, 1:5-1:3, 0:3-2:3]

och 3)

0 1 2 3 4 5 6 0 · · · 1 · · · · · 2 · · · o · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·

Möjlig lösning: [2:1-2:3, 0:2-2:2, 4:1-2:1, 4:3-4:1, 2:3-4:3, 1:4-1: 2, 2:1-2:3, 0:4-0:2, 4:4-4:2, 3:4-1:4, 6:3-4:3, 1:1-1:3, 4:6-4:4, 5:1-3:1, 2:6-2:4, 1:4-1:2, 0:2-2:2, 3:6-3:4, 4: 3-4:1, 6:2-4:2, 2:3-2:1, 4:1-4:3, 5:5-5:3, 2:0-2:2, 2:2- 4:2, 3:4-5:4, 4:3-4:1, 3:0-3:2, 6:4-4:4, 4:0-4:2, 3:2-5: 2, 5:2-5:4, 5:4-3:4, 3:4-1:4, 1:5-1:3]

Brädevarianter

Peg solitaire har spelats på brädor av andra storlekar, även om de två ovanstående är de mest populära. Det har också spelats på en triangulär bräda, med hopp tillåtna i alla 3 riktningar. Så länge varianten har rätt "paritet" och är tillräckligt stor så kommer den troligen att gå att lösa.








Peg solitaire spelplansformer: (1) Fransk (europeisk) stil, 37 hål, 1600-tal; (2) JC Wiegleb, 1779, Tyskland, 45 hål; (3) Asymmetrisk 3-3-2-2 som beskrivs av George Bell, 1900-talet; (4) Engelsk stil (standard), 33 hål; (5) Diamant, 41 hål; (6) Triangulär, 15 hål. Grå = hålet för den överlevande.

En vanlig triangulär variant har fem pinnar på en sida. En lösning där den sista pinnen kommer till det initiala tomma hålet är inte möjlig för ett hål i en av de tre centrala positionerna. En tom hörnhålsuppsättning kan lösas i tio drag, och en tom mitthålsuppsättning i nio (Bell 2008):

TV-spel

Den 26 juni 1992 släpptes ett videospel baserat på peg solitaire för Game Boy. Spelet heter helt enkelt Solitaire och utvecklades av Hect. I Nordamerika släppte DTMC spelet som Lazlos' Leap .

I populärkulturen

Cracker Barrel har spelet vid varje bord på deras platser. Brädan som visas är triangulär med totalt 15 hål.

Vidare läsning

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Peg_solitaire&oldid=1140876906 "