Och–eller träd

Ett och–eller träd är en grafisk representation av reduktionen av problem (eller mål) till konjunktioner och disjunktioner av delproblem (eller delmål).

Exempel

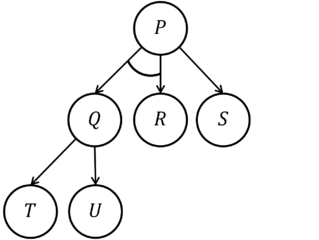
och-eller-trädet:

representerar sökutrymmet för att lösa problemet P, med hjälp av målreduceringsmetoderna:

P om Q och R

P om S

Q om T

Q om U

Definitioner

₀ Givet ett initialt problem P och en uppsättning problemlösningsmetoder i formen:

P om P ₁ och … och P _n

det associerade och-eller-trädet är en uppsättning märkta noder så att:

1. ₀ Trädets rot är en nod märkt med P .
2. För varje nod N märkt av ett problem eller delproblem P och för varje metod av formen P om P ₁ och ... och P _n , finns det en uppsättning barnnoder N ₁ , ..., N _n av noden N, såsom att varje nod Ni _är märkt med _Pi . Noderna är sammanfogade av en båge, för att skilja dem från barn av N som kan vara associerade med andra metoder.

En nod N, märkt med ett problem P, är en framgångsnod om det finns en metod av formen P om ingenting (dvs P är ett "faktum"). Noden är en felnod om det inte finns någon metod för att lösa P.

Om alla barn i en nod N, sammanfogade av samma båge, är framgångsnoder, så är noden N också en framgångsnod. Annars är noden en felnod.

Sökstrategier

Ett och-eller-träd anger endast sökutrymmet för att lösa ett problem. Olika sökstrategier för att söka i utrymmet är möjliga. Dessa inkluderar att söka efter trädets djup-först, bredd-först eller bäst-först med hjälp av ett visst mått av önskvärda lösningar. Sökstrategin kan vara sekventiell, sökning eller generering av en nod i taget, eller parallell, sökning eller generering av flera noder parallellt.

Samband med logisk programmering

Metoderna som används för att generera och-eller träd är propositionella logikprogram (utan variabler). I fallet med logikprogram som innehåller variabler, måste lösningarna av gemensamma delproblem vara kompatibla. Med förbehåll för denna komplikation tillhandahåller sekventiella och parallella sökstrategier för och-eller-träd en beräkningsmodell för exekvering av logikprogram.

Förhållande till spel för två spelare

Och-eller träd kan också användas för att representera sökutrymmen för två-personers spel. Rotnoden i ett sådant träd representerar problemet med att en av spelarna vinner spelet, med början från spelets initiala tillstånd. Givet en nod N, märkt med problemet P med spelaren som vinner spelet från ett visst spelläge, finns det en enda uppsättning av sammanfogade barnnoder, som motsvarar alla motståndarnas svar på drag. För var och en av dessa barnnoder finns det en uppsättning icke-sammanhängande barnnoder, motsvarande alla spelarens försvarsdrag.

För att lösa spelträd med provnummersökningsfamilj av algoritmer, ska spelträd mappas till och-eller träd. MAX-noder (dvs. maximera spelaren att flytta) representeras som ELLER-noder, MIN-noder mappas till OCH-noder. Kartläggningen är möjlig när sökningen görs med endast ett binärt mål, vilket vanligtvis är "spelare att flytta vinner spelet".

Bibliografi

•   Luger, George F.; Stubblefield, William A. (1993). Artificiell intelligens: strukturer och strategier för komplex problemlösning ( 2 uppl.). Benjamin/Cummings. ISBN 978-0-8053-4785-2 . Hämtad 28 februari 2013 .
•   Nilsson, Nils J. (1998). Artificiell intelligens: en ny syntes . Morgan Kaufmann. ISBN 978-1-55860-467-4 . Hämtad 28 februari 2013 .