Neyman konstruktion

Neyman-konstruktion , uppkallad efter Jerzy Neyman , är en frekventistisk metod för att konstruera ett intervall på en konfidensnivå $C,\,$ så att om vi upprepar experimentet många gånger kommer intervallet att innehålla det sanna värdet av någon parameter a bråkdel $C\,$ av tiden.

Teori

Antag $X_{1},X_{2},...X_{n}$ är slumpvariabler med gemensam pdf $f(x_{1},x_{2},...x_{n}|\theta _{1},\theta _{2},...,\theta _ {k})$ , vilket beror på k okända parametrar. För enkelhetens skull, låt $) {\displaystyle X=(X_{1},X_{2},...X_{n})}$$\displaystyle \Theta }$ vara sampelutrymmet som definieras av de n slumpvariablerna och definiera därefter en provpunkt i sampelutrymmet som Neyman föreslog ursprungligen att definiera två funktioner $L(x)$ och $U( x)$ så att för valfri provpunkt, $X$ ,

• $L(X)\leq U(X)$$\forall X\in \Theta$
• L och U är enkelvärderade och definierade.

Givet en observation, $X^{'}$ , är sannolikheten att $\theta _{1}$ ligger mellan $L(X^{'})$ och $U(X^{'})$ definieras som $P(L(X^ {'})\leq \theta _{1}\leq U(X^{'})|X^{'})$ med sannolikheten $0$ eller $1$ . Dessa beräknade sannolikheter misslyckas med att dra meningsfulla slutsatser om $\theta _{1}$ eftersom sannolikheten helt enkelt är noll eller enhet. Vidare, under den frekventistiska konstruktionen är modellparametrarna okända konstanter och får inte vara slumpvariabler. Till exempel om $\theta _{1}=5$ , då $P(2\leq 5\leq 10)=1$ . På samma sätt, om $\theta _{1}=11$ , då $P(2\leq 11\leq 10)=0$

Som Neyman beskriver i sin uppsats från 1937, anta att vi betraktar alla punkter i provutrymmet, det vill säga $\forall X\in \Theta$ , som är ett system av slumpvariabler som definieras av den gemensamma pdf-filen beskrivs ovan. Eftersom $L$ och $U$ är funktioner av $X$ är de också slumpvariabler och man kan undersöka innebörden av följande sannolikhetssats:

Under den frekventistiska konstruktionen är modellparametrarna okända konstanter och får inte vara slumpvariabler. Om man betraktar alla provpunkter i provrummet som slumpvariabler definierade av den gemensamma pdf-filen ovan, det vill säga alla $X\in \Theta$ kan det visas att $L$ och $U$ är funktioner av slumpvariabler och därmed slumpvariabler. Därför kan man titta på sannolikheten för $L(X)$ och $U(X)$ för några $X\in \Theta$ . Om $\theta _{1}^{'}$ är det sanna värdet av $\theta _{1}$ , kan vi definiera $L$ och $U$ så att sannolikheten $L(X)\leq \theta _{1}^{'}$ och $\theta _{ 1}^{'}\leq U(X)$ är lika med fördefinierad konfidensnivå $,C$ .

Det vill säga $P(L(X)\leq \theta _{1}^{'}\leq U( X)|\theta _{1}^{'})=C$ där $0\leq C\leq 1$ och $L(X)$ och $U(X)$ är de övre och nedre konfidensgränserna för $\theta _{1}$

Täckningssannolikhet

Täckningssannolikheten , $C$ , för Neyman-konstruktion är frekvensen av experiment där konfidensintervallet innehåller det faktiska värdet av intresse . I allmänhet är täckningssannolikheten inställd på $95\%$ konfidens. För Neyman-konstruktion är täckningssannolikheten satt till något värde $C$ där $0<C<1$ . Detta värde $C$ talar om hur säkra vi är på att det sanna värdet kommer att finnas i intervallet.

Genomförande

En Neyman-konstruktion kan utföras genom att utföra flera experiment som konstruerar datamängder som motsvarar ett givet värde på parametern. Experimenten är utrustade med konventionella metoder och utrymmet för anpassade parametervärden utgör det band som konfidensintervallet kan väljas från.

Klassiskt exempel

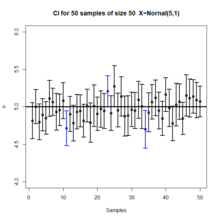
Plotta med 50 konfidensintervall från 50 sampel genererade från en normalfördelning.

Antag att $X\sim N(\theta ,\sigma ^{2})$ , där $\theta$ och $\sigma ^{2}$ är okända konstanter där vi vill uppskatta $\theta$ . Vi kan definiera (2) enstaka värdefunktioner, $L$ och $U$ , definierade av processen ovan så att givet en fördefinierad konfidensnivå, $C$ och slumpmässigt urval $X^{*}=(x_{1},x_{2},...x_{n})$

$L(X^{*})={\bar {x}}-t{\frac {s}{\sqrt {n}}}$

$U(X^{*})={\bar {x}}+t{\frac {s}{\sqrt {n}}}$

där $s/{\sqrt {n}}$ är standardfelet och urvalets medelvärde och standardavvikelse är:

${\bar {x}}={\frac {1}{n}}\ summa _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1},x_{2},...x_{n})$

$s={\sqrt {{\frac {1}{n-1}}\summa _{i=1}^{n}(x_ {i}-{\bar {x}})^{2}}}$

Faktorn $t$ följer en t- fördelning med (n-1) frihetsgrader, $t$ ~t _{$({1-C} /2,n-1)$}

Ett annat exempel

$,...,X_{n}}$${\ displaystil T=(X_{1},X_{2},...,X_{n})}$ är iid slumpvariabler, och låt . Antag $T\sim N(\mu ,\sigma ^{2})$ . Nu för att konstruera ett konfidensintervall med $C$ konfidensnivå. Vi vet att ${\bar {x}}$ är tillräckligt för $\mu$ . Så,

$p(-Z_{\frac {\alpha }{2}}\leq {\frac {{\bar {x} }-\mu }{\sigma ^{2}}}\leq Z_{\frac {\alpha }{2}})=C$

$p(-Z_{\frac {\alpha }{2}}\sigma ^{2}\leq {\bar {x}}-\mu \leq Z_{\frac {\alpha } {2}}\sigma ^{2})=C$

$p({\bar {x}} -Z_{\frac {\alpha }{2}}\sigma ^{2}\leq \mu \leq {\bar {x}}+Z_{\frac {\alpha }{2}}\sigma ^{2 })=C$

Detta ger ett $100(C)\%$ konfidensintervall för $\mu$ där,

$L(T)={\bar {x}}-Z_{\frac {\alpha }{2}}\sigma ^{2}$

$U(T)={\bar {x}}+Z_{\frac {\alpha }{2}}\sigma ^{2}$ .

Se även

• Sannolikhetstolkningar