Multiträd

Ej att förväxla med MultiTree .

Fjärilsnätverket , ett multiträd som används i distribuerad beräkning, som visar i rött det oriktade trädet som induceras av subgrafen som kan nås från en av dess hörn .

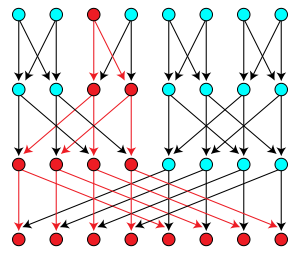
Inom kombinatorik och ordningsteoretisk matematik kan ett multiträd beskriva endera av två ekvivalenta strukturer: en riktad acyklisk graf (DAG) där det finns högst en riktad bana mellan vilka två hörn som helst , eller på motsvarande sätt där subgrafen som kan nås från vilken hörn som helst inducerar ett oriktat träd , eller en delvis ordnad uppsättning (poset) som inte har fyra poster a , b , c och d som bildar en diamantunderordning med a ≤ b ≤ d och a ≤ c ≤ d men med b och c ojämförbara med varje annan (även kallad en diamantfri poset ).

I beräkningskomplexitetsteorin har multiträd också kallats starkt entydiga grafer eller mangrover ; de kan användas för att modellera icke-deterministiska algoritmer där det finns högst en beräkningsväg som förbinder två tillstånd.

Multiträd kan användas för att representera flera överlappande taxonomier över samma grunduppsättning. Om ett släktträd kan innehålla flera äktenskap från en familj till en annan, men inte innehåller äktenskap mellan två släktingar, bildar det ett multiträd.

Likvärdighet mellan DAG- och posets definitioner

I en riktad acyklisk graf, om det finns högst en riktad bana mellan två hörn, eller ekvivalent om subgrafen som kan nås från någon vertex inducerar ett oriktat träd, så är dess nåbarhetsrelation en diamantfri partiell ordning. Omvänt, i en partiell ordning, om den är diamantfri, identifierar dess transitiva reduktion en riktad acyklisk graf där subgrafen som kan nås från vilken vertex som helst inducerar ett oriktat träd.

Diamantfria familjer

En diamantfri familj av set är en familj F av set vars inkluderande ordning bildar en diamantfri poset. Om D ( n ) betecknar den största möjliga diamantfria familjen av delmängder av en n -elementmängd, då är det känt att

$2\leq \lim _{n\to \infty }D(n){\Big /}{\ binom {n}{\lfloor n/2\rfloor }}\leq 2{\frac {3}{11}}$

och det antas att gränsen är 2.

Relaterade strukturer

Ett polyträd , en riktad acyklisk graf som bildas genom att orientera kanterna på ett oriktat träd, är ett specialfall av ett multiträd.

Subgrafen som kan nås från vilken vertex som helst i ett multiträd är en arborescens som är rotad i vertexen, det vill säga ett polyträd där alla kanter är orienterade bort från roten.

Ordet "multitree" har också använts för att hänvisa till en serieparallell partiell ordning , eller till andra strukturer som bildas genom att kombinera flera träd.