Minsta flaskhalsspännande träd

Inom matematik är ett minimum flaskhalsspannträd (MBST) i en oriktad graf ett spännträd där den dyraste kanten är så billig som möjligt. En flaskhalskant är den högst viktade kanten i ett spännträd. Ett spannträd är ett minsta flaskhalsspännande träd om grafen inte innehåller ett spännträd med en mindre flaskhalskantvikt. För en riktad graf är ett liknande problem känt som Minimum Bottneck Spanning Arborescence (MBSA) .

Definitioner

Oriktade grafer

Minimal flaskhalsspännande träd

G(V,E)

I en oriktad graf _G $(V, E) och$ en funktion $w : E \to R$ , låt $S$ vara mängden av alla spännande träd Ti . Låt B ( Ti ) vara _den maximala viktkanten för varje _spännträd Ti . Vi definierar en delmängd av minsta flaskhalsspännande träd S ′ så att för varje $T j \in S'$ och $T k \in S$ har vi $B (T j) \leq B (T k)$ för alla i och k .

Grafen till höger är ett exempel på MBST, de röda kanterna i grafen bildar en MBST av $G (V, E)$ .

Riktade grafer

Minimal flaskhalsspännande arborescens G(V,E)

En arborescens av graf G är ett riktat träd av G som innehåller en riktad väg från en specificerad nod L till varje nod i en delmängd V ′ av $V \{ L }$ . Nod L kallas roten till arborescens. En arborescens är en spännande arborescens om $V ′ = V \{ L }$ . MBST i detta fall är en spännande arborescens med minsta flaskhalskant. En MBST i detta fall kallas en Minimum Bottleneck Spanning Arborescence (MBSA).

Grafen till höger är ett exempel på MBSA, de röda kanterna i grafen bildar en MBSA av $G (V, E)$ .

Egenskaper

En MST (eller minimum spanning tree ) är nödvändigtvis en MBST, men en MBST är inte nödvändigtvis en MST.

Camerinis algoritm för oriktade grafer

Camerini föreslog en algoritm som användes för att erhålla ett minsta flaskhalsspannträd (MBST) i en given oriktad, ansluten, kantviktad graf 1978. Den delar upp kanterna till hälften i två uppsättningar. Kanternas vikt i en uppsättning är inte mer än i den andra. Om ett spännträd finns i subgrafen som enbart består av kanter i mindre kanter, beräknar den sedan en MBST i subgrafen, en MBST för subgrafen är exakt en MBST av den ursprungliga grafen. Om ett spännträd inte finns, kombinerar det varje frånkopplad komponent till en ny supervertex, och beräknar sedan en MBST i grafen som bildas av dessa superhörn och kanter i de större kanterna. En skog i varje frånkopplad komponent är en del av en MBST i originalgraf. Upprepa denna process tills två (super) hörn finns kvar i grafen och en enda kant med minsta vikt mellan dem ska läggas till. En MBST hittas som består av alla kanter som hittats i tidigare steg.

Pseudokod

Proceduren har två ingångsparametrar. G är en graf, w är en viktuppsättning av alla kanter i grafen G .

 
       
        
        
         
            
              funktion  MBST(graf  G  , vikter  w  )  E  ← uppsättningen kanter av  G  om  |  E  | = 1   returnera  sedan  E  annat  A  ← halvkanter i  E vars   vikter  inte är mindre än medianvikten  B  ←  E  -  A  F  ← skog av  G _B om  F  är ett spännträd  returnera  MBST(  G _B ,  w  )  returnera  annars  MBST ((  GA  ) _η ,  w  )  $\displaystyle \cup }$ _{ F

I ovanstående ( GA ) är _η subgrafen sammansatt av superhörn (genom att betrakta hörn i en frånkopplad komponent som en) och kanter _i A .

Körtid

Algoritmen körs i O ( E ) tid, där E är antalet kanter. Denna gräns uppnås enligt följande:

uppdelning i två uppsättningar med medianfyndande algoritmer i O ( E )
hitta en skog i O ( E )
med tanke på halvkanter i E i varje iteration O ( E + E /2 + E /4 + ··· + 1) = O ( E )

Exempel

I följande exempel används gröna kanter för att bilda en MBST och streckade röda områden indikerar superhörn som bildas under algoritmstegen.

	Algoritmen delar upp kanterna i två uppsättningar med avseende på vikter. Gröna kanter är de kanter vars vikter är så små som möjligt.
	Eftersom det finns ett spännträd i subgrafen bildat enbart med kanter i de mindre kanterna satta. Upprepa att hitta en MBST i denna subgraf.
	Eftersom det inte finns ett spännträd i den aktuella subgrafen bildad med kanter i den aktuella mindre kanternas uppsättning. Kombinera hörnen av en frånkopplad komponent till en superhörn (betecknad med ett streckat rött område) och hitta sedan en MBST i subgrafen som bildas med superhörn och kanter i större kanter satta. En skog som bildas inom varje frånkopplad komponent kommer att vara en del av en MBST i den ursprungliga grafen.
	Upprepa liknande steg genom att kombinera fler hörn till en super vertex.
	Algoritmen erhåller slutligen en MBST genom att använda kanter som den hittade under algoritmen.

MBSA-algoritmer för riktade grafer

Det finns två algoritmer tillgängliga för riktade grafer: Camerinis algoritm för att hitta MBSA och en annan från Gabow och Tarjan.

Camerinis algoritm för MBSA

För en riktad graf fokuserar Camerinis algoritm på att hitta den uppsättning kanter som skulle ha sin maximala kostnad som flaskhalskostnaden för MBSA. Detta görs genom att dela upp uppsättningen av kanter E i två uppsättningar A och B och bibehålla uppsättningen T som är den uppsättning där det är känt att G _T inte har en spännande arborescens, vilket ökar T med B närhelst den maximala arborescensen för G ( B ∪ T ) är inte en sträckande arborescens av G , annars minskar vi E med A . Den totala tidskomplexiteten är O ( E log E ).

Pseudokod

     
    
        
          funktion  MBSA(  G  ,  w  ,  T  )  är  E  ← uppsättningen kanter av  G  if  |  E − T  | > 1   sedan  A  ← UH(ET)  B  ← (  E − T)  −  A  F  ← BUSH(  G _BUT )  om  F  är en spännande arborescens av G  då  S ← F MBSA((  G _BUT ),  w  ,  T  )  annars  MBSA (G,  w  ,  TUB  );

T representerar en delmängd av E för vilken det är känt att GT _inte innehåller någon spännande arborescens rotad vid nod "a". Till en början är T tomt
UH tar (E−T) uppsättning kanter i G och returnerar A ⊂ (E−T) så att:
1. $|A|=\left\lfloor {\frac {(|ET|)}{2}}\right\rfloor$
2. W _a ≥ W _b , för a ∈ A och b ∈ B
BUSH(G) returnerar en maximal arborescens av G rotad vid nod "a"
Slutresultatet blir S

Exempel

	Efter att ha kört den första iterationen av denna algoritm får vi att $F$ och $F$ inte är en spännande arborescens av $G$ , så vi kör koden $MBSA(G,w,T\cup B).$
	I den andra iterationen får vi $F'$ och $F'$ är inte heller en spännande arborescens av $G$ , Så vi kör koden $MBSA(G,w,T'\cup B')$
	I den tredje iterationen får vi $F''$ och $F''$ är en spännande arborescens av $G$ , så vi kör koden $MBSA(G_{ T''\cup B''},w,T'')$
	när vi kör $MBSA(G_{T''\cup B''},w,T'')$ , den $\|ET\|$ är lika med 1, vilket inte är större än 1, så algoritmen returnerar och slutresultatet är $S=F''$ .

Gabow och Tarjan-algoritm för MBSA

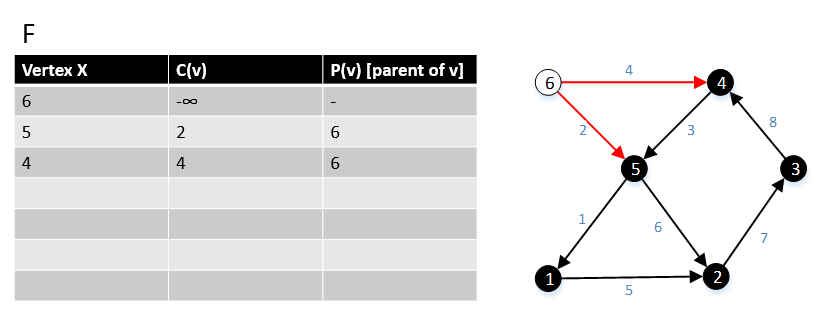
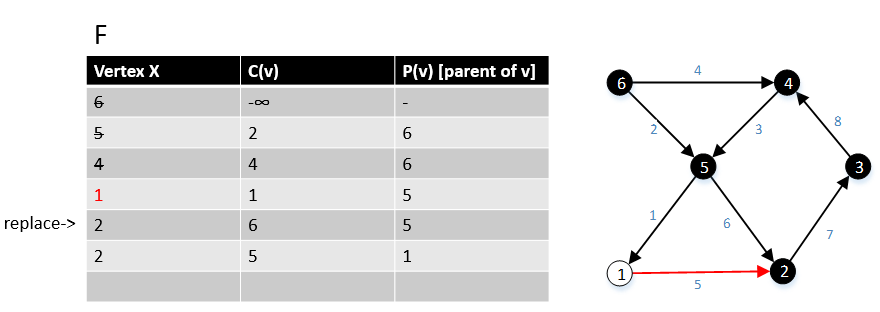
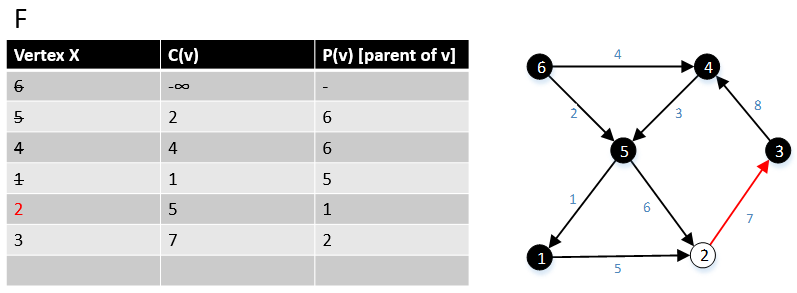
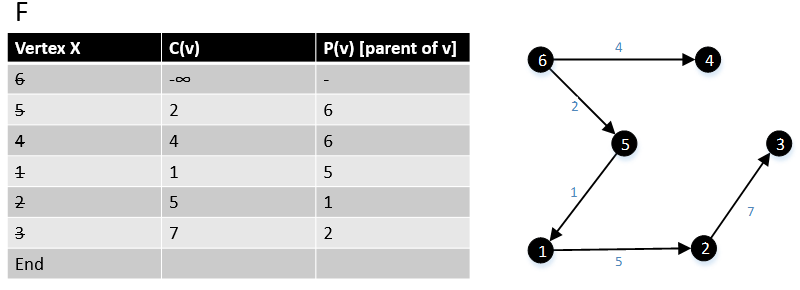
Gabow och Tarjan tillhandahöll en modifiering av Dijkstras algoritm för en källas kortaste väg som producerar en MBSA. Deras algoritm körs i O ( E + V log V ) tid om Fibonacci-hög används.

Pseudokod

    För en graf  G(V,E)  är F en samling av hörn i  V  . Inledningsvis   F  = {  s  } där  s  är startpunkten för grafen  G  och  c  (  s  ) = -∞ 1  funktion  MBSA-GT(  G  ,  w, T  ) 2  repeat  |V| gånger 3 Välj   v  med minimum  c  (  v  ) från  F  ; 4 Ta bort det från   F  ; 5   för  ∀ kant(  v, w  )  gör  6  om  w  ∉  F  eller ∉ Träd ,   lägg  till  w  till  F;  8  c  (  w  ) =  c  (  v,w  ); 9   p  (  w  ) =  v  ; 10   annars  11  om  w  ∈  F  och  c(w) > c(v, w)  så är  12  c  (  w  ) =  c  (  v, w  ); 13   p  (  w  ) =  v  ;

Exempel

Följande exempel visar hur algoritmen fungerar.

I det första steget av algoritmen väljer vi roten s från grafen G, i ovanstående figur är vertex 6 roten s. Sedan hittade vi all edge(6,w) ∈ E och deras kostnad c(6,w), där w ∈ V.

Därefter flyttar vi till vertex 5 i grafen G, vi hittade hela edge(5,w) ∈ E och deras kostnad c(5,w), där w ∈ V.

Därefter flyttar vi till vertex 4 i grafen G, vi hittade hela edge(4,w) ∈ E och deras kostnad c(4,w) , där w ∈ V. Vi finner att edge(4,5) > edge(6.5), så vi behåller edge(6,5) och tar bort kanten(4,5).

Därefter går vi till vertex 1 i grafen G, vi hittade alla edge(1,w) ∈ E och deras kostnad c(1,w), där w ∈ V. Vi finner att edge(5,2) > edge(1,2), så vi tar bort edge(5,2) och behåller kanten(1,2).

Därefter flyttar vi till vertex 2 i grafen G, vi hittade alla edge(2,w) ∈ E och deras kostnad c(2,w), där w ∈ V. Därefter flyttar vi till vertex 3 i grafen

G , vi hittade alla edge(3,w) ∈ E och deras kostnad c(3,w), där w ∈ V. Vi finner att edge(3,4) > edge(6,4), så vi tar bort kant(3,4) och behåll kanten(6,4).

Efter att vi går igenom alla hörn i grafen G har algoritmen slutförts.

Ett annat tillvägagångssätt som föreslagits av Tarjan och Gabow med gränsen för $O (E log * V)$ för glesa grafer, där det är mycket likt Camerinis algoritm för MBSA, men snarare än att partitionera uppsättningen av kanter i två uppsättningar per varje iteration, $K (i)$ introducerades där i är antalet delningar som har skett eller med andra ord iterationstalet, och $K (i)$ är en ökande funktion som betecknar antalet partitionerade uppsättningar som man ska ha per iteration. $K (i) = 2 k (i - 1)$ med $k (1) = 2$ . Algoritmen hittar $λ *$ där det är värdet på flaskhalskanten i vilken MBSA som helst. Efter att $λ *$ har hittats är eventuell spännande arborescens i $G (λ *)$ en MBSA där $G (λ *)$ är grafen där alla dess kantkostnader är $\leq λ *$ .