Mandelstam variabler

I det här diagrammet kommer två partiklar in med momenta p ₁ och p ₂ , de interagerar på något sätt och sedan lämnar två partiklar med olika momentum (p ₃ och p _{4 ).}

I teoretisk fysik är Mandelstam -variablerna numeriska storheter som kodar partiklarnas energi , rörelsemängd och vinklar i en spridningsprocess på ett Lorentz-invariant sätt. De används för spridningsprocesser av två partiklar till två partiklar. Mandelstam-variablerna introducerades först av fysikern Stanley Mandelstam 1958.

Om Minkowski-måttet väljs att vara $\mathrm {diag} (1,-1,-1,-1)$ , Mandelstam-variablerna $s,t,u$ definieras sedan av

$s=(p_{1}+p_{2})^{2}c^{2}=( p_{3}+p_{4})^{2}c^{2}$
$t=(p_{1}-p_{3})^{2}c^{2}=( p_{4}-p_{2})^{2}c^{2}$
$u=(p_{1}-p_{4})^{2}c^{2}=( p_{3}-p_{2})^{2}c^{2}$ ,

där p ₁ och p ₂ är fyra momenta för de inkommande partiklarna och p ₃ och p ₄ är fyra momenta för de utgående partiklarna.

$s$ är också känd som kvadraten av masscentrumenergin ( invariant massa ) och $t$ som kvadraten av fyra-momentumöverföringen .

Feynman-diagram

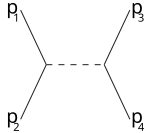
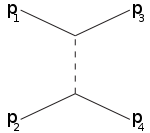
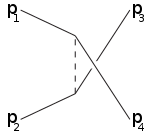
Bokstäverna s,t,u används också i termerna s-kanal (tidsliknande kanal), t-kanal och u-kanal (båda rymdliknande kanaler). Dessa kanaler representerar olika Feynman-diagram eller olika möjliga spridningshändelser där interaktionen involverar utbyte av en mellanliggande partikel vars kvadratiska fyrmomentum är lika med s,t,u respektive.


s-kanal	t-kanal	u-kanal

Till exempel motsvarar s-kanalen att partiklarna 1,2 förenas till en mellanliggande partikel som så småningom delas upp i 3,4: s-kanalen är det enda sättet som resonanser och nya instabila partiklar kan upptäckas förutsatt att deras livstid är tillräckligt lång att de är direkt detekterbara. ^{[ citat behövs ]} t-kanalen representerar processen där partikel 1 avger mellanpartikeln och blir den slutliga partikeln 3, medan partikel 2 absorberar mellanpartikeln och blir 4. U-kanalen är t-kanalen med roll partiklarna 3,4 utbytta.

När man utvärderar en Feynman-amplitud hittar man ofta skalära produkter av de yttre fyra momenta. Man kan använda Mandelstam-variablerna för att förenkla dessa:

$p_{1}\cdot p_{2}={\frac {s/c^{2}-m_{1}^ {2}-m_{2}^{2}}{2}}$

$p_{1}\cdot p_{3}={\frac {m_{1}^{2}+m_{3} ^{2}-t/c^{2}}{2}}$

$p_{1}\cdot p_{4}={\frac {m_{1}^{2}+m_{4} ^{2}-u/c^{2}}{2}}$

Där $m_{i}$ är massan av partikeln med motsvarande rörelsemängd $p_{i}$ .

Belopp

Anteckna det

(s+t+u)/c^{2}=m_{1}^{2 }+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}

där m _i är massan av partikel i .

Bevis

För att bevisa detta måste vi använda två fakta:

Kvadraten på en partikels fyra rörelsemängd är kvadraten på dess massa,

p_{i}^{2}=m_{i}^{2}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1)

Och bevarande av fyrmomentum,

p_{1}+p_{2} =p_{3}+p_{4}

p_{1}=-p_{2}+p_{3}+p_{4}\ quad \quad \quad \quad \quad \quad \,\,(2)

Så till att börja,

s/c^{2}=(p_{1}+p_{2}) ^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}

t/c^{2}=(p_{1}-p_{3})^{2}=p_{1}^{2}+p_{ 3}^{2}-2p_{1}\cdot p_{3}

u /c^{2}=(p_{1}-p_{4})^{2}=p_{1}^{2}+p_{4}^{2}-2p_{1}\cdot p_{4 }

Att sedan lägga till de tre samtidigt som du sätter in kvadratiska massor leder till,

(s+t+u)/c^{2}=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4} ^{2}+2p_{1}^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}

Lägg sedan märke till att de fyra sista termerna summerar till noll med bevarande av fyra momentum,

2p_{1 }^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}=2p_{1}\cdot (p_{1} +p_{2}-p_{3}-p_{4})=0

Så äntligen,

(s+t+u)/c^{2}=m_{1}^{2 }+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}

.

Relativistisk gräns

I den relativistiska gränsen är rörelsemängden (hastigheten) stor, så med den relativistiska energi-momentum-ekvationen blir energin i huvudsak rörelsemängdsnormen (t.ex. $E^{2}=\ mathbf {p} \cdot \mathbf {p} +{m_{0}}^{2}$ blir $E^{2}\approx \mathbf {p} \cdot \mathbf { p}$ ). Vilomassan kan också försummas.

Så t.ex.

s/c^{2}=(p_{1 }+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}\approx 2p_{1}\cdot p_{ 2}

eftersom $p_{1}^{2}=m_{1}^{2}$ och $p_{2}^{2}=m_ {2}^{2}$ .

Således,

$s/c^{2}\approx$	$2p_{1}\cdot p_{2}\approx$	$2p_{3}\cdot p_{4}$
$t/c^{2}\approx$	$-2p_{1}\cdot p_{3}\approx$	$-2p_{2}\cdot p_{4}$
$u/c^{2}\approx$	$-2p_{1}\cdot p_{4}\approx$	$-2p_{3}\cdot p_{2}$