Linjär klassificerare

Inom området maskininlärning är målet med statistisk klassificering att använda ett objekts egenskaper för att identifiera vilken klass (eller grupp) det tillhör. En linjär klassificerare uppnår detta genom att fatta ett klassificeringsbeslut baserat på värdet av en linjär kombination av egenskaperna. Ett objekts egenskaper är också kända som funktionsvärden och presenteras vanligtvis för maskinen i en vektor som kallas en egenskapsvektor . Sådana klassificerare fungerar bra för praktiska problem som dokumentklassificering , och mer allmänt för problem med många variabler ( funktioner ), och når noggrannhetsnivåer jämförbara med icke-linjära klassificerare samtidigt som det tar mindre tid att träna och använda.

Definition

I det här fallet kan de solida och tomma prickarna klassificeras korrekt med valfritt antal linjära klassificerare. H1 (blå) klassificerar dem korrekt, liksom H2 (röd). H2 skulle kunna anses vara "bättre" i den meningen att den också är längst ifrån båda grupperna. H3 (grön) klassificerar inte prickarna korrekt.

Om ingångsvektorn till klassificeraren är en reell vektor ${\displaystyle {\vec {x}}},$ så är utdatapoängen

y=f({\vec {w}}\cdot {\vec {x}})=f\left( \sum _{j}w_{j}x_{j}\right),

där ${\vec {w}}$ är en reell vektor av vikter och f är en funktion som omvandlar punktprodukten av de två vektorerna till önskad utdata. (Med andra ord, ${\vec {w}}$ är en enforms eller linjär funktionell mappning ${\vec {x}}$ på R .) Viktvektorn ${\vec {w}}$ lärs från en uppsättning märkta träningsexempel. Ofta f en tröskelfunktion , som mappar alla värden på ${\vec {w}}\cdot {\vec {x}}$ över en viss tröskel till den första klassen och alla andra värden till tvåan; t.ex,

f(\mathbf {x} )={\begin{cases}1&{\text{if }}\ \mathbf {w} ^{ T}\cdot \mathbf {x} >\theta ,\\0&{\text{annars}}\end{fall}}

Det upphöjda T indikerar transponeringen och $\theta$ är en skalär tröskel. Ett mer komplext f kan ge sannolikheten att ett föremål tillhör en viss klass.

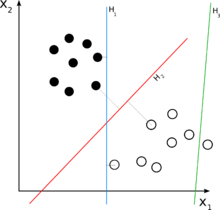
För ett klassificeringsproblem med två klasser kan man visualisera driften av en linjär klassificerare som att dela ett högdimensionellt ingångsutrymme med ett hyperplan : alla punkter på ena sidan av hyperplanet klassificeras som "ja", medan de andra klassificeras som "Nej".

En linjär klassificerare används ofta i situationer där klassificeringshastigheten är ett problem, eftersom det ofta är den snabbaste klassificeraren, speciellt när ${\vec {x}}$ är gles. Linjära klassificerare fungerar också ofta mycket bra när antalet dimensioner i ${\vec {x}}$ är stort, som i dokumentklassificering , där varje element i ${\vec {x} }$ är vanligtvis antalet förekomster av ett ord i ett dokument (se dokumenttermmatris ) . I sådana fall bör klassificeraren vara välregulerad .

Generativa modeller kontra diskriminerande modeller

Det finns två breda klasser av metoder för att bestämma parametrarna för en linjär klassificerare ${\vec {w}}$ . De kan vara generativa och diskriminerande modeller. Metoder för den förra modellen gemensam sannolikhetsfördelning , medan metoder för den senare modellen villkorliga densitetsfunktioner $P({\rm {klass}}|{\vec {x}})$ . Exempel på sådana algoritmer inkluderar:

Linear Discriminant Analysis (LDA) – antar gaussiska villkorliga densitetsmodeller
Naiv Bayes-klassificerare med multinomial eller multivariat Bernoulli-händelsemodeller.

Den andra uppsättningen metoder inkluderar diskriminerande modeller , som försöker maximera kvaliteten på resultatet på en träningsuppsättning . Ytterligare termer i utbildningskostnadsfunktionen kan enkelt utföra regularisering av den slutliga modellen. Exempel på diskriminerande träning av linjära klassificerare inkluderar:

Logistisk regression — maximal sannolikhetsuppskattning av ${\vec {w}}$ under antagande att den observerade träningsuppsättningen genererades av en binomial modell som beror på utdata från klassificeraren.
Perceptron — en algoritm som försöker fixa alla fel som uppstår i träningsuppsättningen
Fisher's Linear Discriminant Analysis – en algoritm (annorlunda än "LDA") som maximerar förhållandet mellan klassspridning och spridning inom klassen, utan några andra antaganden. Det är i huvudsak en metod för dimensionalitetsreduktion för binär klassificering.
Stödvektormaskin — en algoritm som maximerar marginalen mellan beslutshyperplanet och exemplen i träningsuppsättningen.

Obs: Trots sitt namn tillhör LDA inte klassen av diskriminerande modeller i denna taxonomi. Dess namn är dock vettigt när vi jämför LDA med den andra huvudsakliga linjära dimensionsreduktionsalgoritmen : huvudkomponentanalys ( PCA). LDA är en övervakad inlärningsalgoritm som använder etiketterna för data, medan PCA är en oövervakad inlärningsalgoritm som ignorerar etiketterna. För att sammanfatta är namnet en historisk artefakt.

Diskriminerande träning ger ofta högre noggrannhet än att modellera de villkorade densitetsfunktionerna [ ^{citat behövs ]} . Men att hantera saknad data är ofta lättare med modeller med villkorad densitet [ ^{citation needed ]} .

Alla linjära klassificeringsalgoritmer som listas ovan kan konverteras till icke-linjära algoritmer som fungerar på ett annat inmatningsutrymme ${\displaystyle \varphi ({\vec {x}})} ,$ med hjälp av kärntricket .

Diskriminerande träning

Diskriminerande träning av linjära klassificerare sker vanligtvis på ett övervakat sätt, med hjälp av en optimeringsalgoritm som ges en träningsuppsättning med önskade utgångar och en förlustfunktion som mäter diskrepansen mellan klassificerarens utdata och de önskade utsignalerna. Således löser inlärningsalgoritmen ett optimeringsproblem av formen

{\underset {\mathbf {w} }{\arg \min }}\;R(\ mathbf {w} )+C\summa _{i=1}^{N}L(y_{i},\mathbf {w} ^{\mathsf {T}}\mathbf {x} _{i})

var

$w$ är en vektor av klassificerare parametrar,
$L (y i, w T x i)$ är en förlustfunktion som mäter diskrepansen mellan klassificerarens förutsägelse och den sanna utsignalen $y i$ för det $i$ :te träningsexemplet,
$R (w)$ är en regleringsfunktion som förhindrar att parametrarna blir för stora (orsakar överanpassning) och
$C$ är en skalär konstant (inställd av användaren av inlärningsalgoritmen) som styr balansen mellan regulariseringen och förlustfunktionen.

Populära förlustfunktioner inkluderar gångjärnsförlusten (för linjära SVM) och logförlusten ( för linjär logistisk regression). Om regulariseringsfunktionen $R$ är konvex är ovanstående ett konvext problem . Det finns många algoritmer för att lösa sådana problem; populära för linjär klassificering inkluderar ( stokastisk ) gradientnedstigning , L-BFGS , koordinatnedstigning och Newtonmetoder .

Se även

Anteckningar

^ ^a ^b ^c Guo-Xun Yuan; Chia-Hua Ho; Chih-Jen Lin (2012). "Senaste framstegen med storskalig linjär klassificering" (PDF) . Proc. IEEE . 100 (9).
^ T. Mitchell, generativa och diskriminerande klassificerare: Naiva Bayes och logistisk regression. Utkastversion, 2005
^ AY Ng och MI Jordan. Om diskriminerande vs. generativa klassificerare: En jämförelse mellan logistisk regression och naiva Bayes. i NIPS 14, 2002.
^ RO Duda, PE Hart, DG Stork, "mönsterklassificering", Wiley, (2001). ISBN 0-471-05669-3
^ RO Duda, PE Hart, DG Stork, "mönsterklassificering", Wiley, (2001). ISBN 0-471-05669-3

Vidare läsning

Y. Yang, X. Liu, "A re-examination of text categorization", Proc. ACM SIGIR Conference, s. 42–49, (1999). papper @ citeseer
R. Herbrich, "Learning Kernel Classifiers: Theory and Algorithms," MIT Press, (2001). ISBN 0-262-08306-X

[ieee-1] Guo-Xun Yuan; Chia-Hua Ho; Chih-Jen Lin (2012). "Senaste framstegen med storskalig linjär klassificering" (PDF) . Proc. IEEE . 100 (9).

[2] T. Mitchell, generativa och diskriminerande klassificerare: Naiva Bayes och logistisk regression. Utkastversion, 2005

[3] AY Ng och MI Jordan. Om diskriminerande vs. generativa klassificerare: En jämförelse mellan logistisk regression och naiva Bayes. i NIPS 14, 2002.

[4] RO Duda, PE Hart, DG Stork, "mönsterklassificering", Wiley, (2001). ISBN 0-471-05669-3

[5] RO Duda, PE Hart, DG Stork, "mönsterklassificering", Wiley, (2001). ISBN 0-471-05669-3