Lindleys paradox

Lindleys paradox är en kontraintuitiv situation i statistik där de Bayesianska och frekventistiska synsätten på ett hypotestestningsproblem ger olika resultat för vissa val av den tidigare fördelningen . Problemet med oenigheten mellan de två tillvägagångssätten diskuterades i Harold Jeffreys lärobok från 1939; det blev känt som Lindleys paradox efter att Dennis Lindley kallade oenigheten för en paradox i en tidning från 1957.

Även om de hänvisas till som en paradox , kan de olika resultaten från Bayesianska och frekventistiska tillvägagångssätt förklaras som att de används för att svara på fundamentalt olika frågor, snarare än faktisk oenighet mellan de två metoderna.

Icke desto mindre orsakas skillnaderna mellan det frekventistiska och bayesianska synsättet för en stor klass av tidigare av att signifikansnivån hålls fast: som till och med Lindley insåg, "teorin motiverar inte praxis att hålla signifikansnivån fixerad" och till och med "vissa beräkningar av professor Pearson i diskussionen till den artikeln betonade hur signifikansnivån skulle behöva förändras med urvalsstorleken, om förlusterna och tidigare sannolikheter hölls fasta.'' Faktum är att om det kritiska värdet ökar med urvalsstorleken på lämpligt sätt. snabbt, då blir oenigheten mellan de frekventistiska och Bayesianska metoderna försumbar när urvalsstorleken ökar.

Beskrivning av paradoxen

Resultatet $\textstyle x$ av något experiment har två möjliga förklaringar, hypoteserna $\textstyle H_{0}$ och $\textstyle H_{1}$ och en viss tidigare distribution $\textstyle \pi$ representerar osäkerhet om vilken hypotes som är mer exakt innan man tar hänsyn till $\textstyle x$ .

Lindleys paradox uppstår när

Resultatet $\textstyle x$ är "signifikant" av ett frekventistiskt test av ${\displaystyle \textstyle H_{0}} ,$ vilket indikerar tillräckligt med bevis för att förkasta ${\displaystyle \textstyle H_{0}} ,$ säg, på 5%-nivån, och
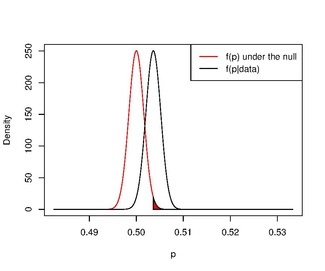
Den bakre sannolikheten för $\textstyle H_{0}$ givet $\textstyle x$ är hög, vilket indikerar starka bevis för att $\textstyle H_{0}$ stämmer bättre överens med ${\ displaystyle \textstyle x}$ än $\textstyle H_{1}$ .

Dessa resultat kan inträffa samtidigt när $\textstyle H_{0}$ är mycket specifik, $\textstyle H_{1}$ mer diffus, och den tidigare fördelningen inte starkt gynnar en eller annat, som ses nedan.

Sifferexempel

Följande numeriska exempel illustrerar Lindleys paradox. I en viss stad har 49 581 pojkar och 48 870 flickor fötts under en viss tidsperiod. Den observerade andelen $\textstyle x$ av mansfödslar är alltså 49 581/98 451 ≈ 0,5036. Vi antar att andelen manliga födslar är en binomial variabel med parametern $\textstyle \theta$ . Vi är intresserade av att testa om $\textstyle \theta$ är 0,5 eller något annat värde. Det vill säga vår nollhypotes är $\textstyle H_{0}:\theta =0.5$ och alternativet är $\textstyle H_{1}:\theta \ neq 0,5$ .

Frekventistiskt tillvägagångssätt

Det frekventistiska tillvägagångssättet för att testa $\textstyle H_{0}$ är att beräkna ett p-värde , sannolikheten för att observera en bråkdel av pojkar som är minst lika stor som $\textstyle x$ med antagande av $\textstyle H_{0}$ är sant. Eftersom antalet födslar är mycket stort kan vi använda en normal approximation för andelen manliga födslar $\textstyle X\sim N(\mu ,\sigma ^{2})$ , med $=n\theta =98 451\ gånger 0,5=49 225,5}$ $theta (1-\theta )=98 451\ gånger 0,5\ gånger 0,5=24 612,75}$ och \

{\begin{aligned}P(X\geq x\mid \mu =49225.5)=\int _{x=49581}^{98451}{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-({\frac {u-\mu }{\sigma }})^{2}/2}du\\=\int _{x=49581}^{98451} {\frac {1}{\sqrt {2\pi (24 612,75)}}}e^{-{\frac {(u-49225.5)^{2}}{24612.75}}/2}du\approx 0,0117.\ end{aligned}}

Vi skulle ha blivit lika förvånade om vi hade sett 49 581 kvinnliga födslar, dvs ${\displaystyle \textstyle x\approx 0,4964} ,$ så en frekventist skulle vanligtvis utföra ett dubbelsidigt test, för vilket p-värdet skulle vara $\textstyle p\approx 2\times 0,0117=0,0235$ . I båda fallen är p-värdet lägre än signifikansnivån, α, på 5 %, så det frekventistiska tillvägagångssättet avvisar $\textstyle H_{0}$ eftersom det inte stämmer överens med de observerade data.

Bayesianskt förhållningssätt

Om man antar att det inte finns någon anledning att gynna den ena hypotesen framför den andra, skulle den Bayesianska metoden vara att tilldela tidigare sannolikheter $\textstyle \pi (H_{0})=\pi (H_) {1})=0.5$ och en enhetlig fördelning till $\textstyle \theta$ under $H_{1}$ , och sedan för att beräkna den bakre sannolikheten för $\textstyle H_{0 }$ med Bayes sats ,

P(H_{0}\mid k)={\frac {P(k\midt H_{0})\pi (H_{0})}{P(k\midt H_{0})\pi (H_{0})+P(k\mid H_{1})\pi (H_{1})}}.

Efter att ha observerat $\textstyle k=49 581$ pojkar av $\textstyle n=98 451$ födslar, kan vi beräkna den bakre sannolikheten för varje hypotes med hjälp av sannolikhetsmassfunktionen för en binomial variabel,

{\begin{aligned}P(k\midt) H_{0})&={n \choose k}(0.5)^{k}(1-0.5)^{nk}\ca 1.95\x 10^{-4}\\P(k\mid H_{1 })&=\int _{0}^{1}{n \choose k}\theta ^{k}(1-\theta )^{nk}d\theta ={n \choose k}\mathrm {\ mathrm {B} } (k+1,n-k+1)=1/(n+1)\approx 1,02\x 10^{-5}\end{aligned}}

där $\textstyle \mathrm {\mathrm {B} } (a,b)$ är Beta-funktionen .

Från dessa värden hittar vi den bakre sannolikheten för ${\displaystyle P(\textstyle H_{0}\mid k)\approx 0.95} ,$ vilket starkt gynnar $\textstyle H_{0 }$ över $\textstyle H_{1}$ .

De två synsätten – den bayesianska och den frekventa – verkar vara i konflikt, och detta är "paradoxen".

Att förena de bayesianska och frekventistiska synsätten

Nästan säker hypotestestning

Naaman föreslog en anpassning av signifikansnivån till provstorleken för att kontrollera falska positiva: $α n$ , så att $α n = n - r$ med $r > 1/2$ . Åtminstone i det numeriska exemplet, att ta $r = 1/2$ , resulterar i en signifikansnivå på 0,00318, så frekventisten skulle inte förkasta nollhypotesen, vilket stämmer överens med Bayesianska synsätt.

Oinformativa föregångare

Fördelning av

p

under nollhypotesen, och den bakre fördelningen av

p

.

Om vi använder en oinformativ prior och testar en hypotes som är mer lik den i det frekventistiska synsättet försvinner paradoxen.

Till exempel, om vi beräknar den bakre fördelningen $\textstyle P(\theta \mid x,n)$ , med hjälp av en enhetlig tidigarefördelning på $\textstyle \theta$ ( dvs ${\displaystyle \textstyle \pi (\theta \in [0,1])=1} ),$ finner vi

P(\theta \mid k,n)=\mathrm {\mathrm {B} } (k+1,n-k+1).

Om vi använder detta för att kontrollera sannolikheten för att en nyfödd är mer sannolikt att vara en pojke än en flicka, dvs $P(\theta >0,5\mid k,n)$ , vi hittar

\int _{0.5}^{1}\mathrm {\mathrm {B} } (49582,48871)\approx 0.983.

Det är med andra ord mycket troligt att andelen manliga födslar är över 0,5.

Ingendera analysen ger direkt en uppskattning av effektstorleken , men båda skulle kunna användas för att till exempel avgöra om andelen pojkfödslar sannolikt ligger över en viss tröskel.

Avsaknaden av en verklig paradox

Den uppenbara oenigheten mellan de två tillvägagångssätten orsakas av en kombination av faktorer. Först testar den frekventistiska metoden ovan $\textstyle H_{0}$ utan hänvisning till $\textstyle H_{1}$ . Den bayesianska metoden utvärderar $\textstyle H_{0}$ som ett alternativ till $\textstyle H_{1}$ och finner att den första överensstämmer bättre med observationerna. Detta beror på att den senare hypotesen är mycket mer diffus, eftersom $\textstyle \theta$ kan vara var som helst i ${\displaystyle \textstyle [0,1]} , vilket resulterar i att$ har en mycket låg posterior sannolikhet. För att förstå varför, är det bra att betrakta de två hypoteserna som generatorer av observationerna:

Under $\textstyle H_{0}$ väljer vi ${\displaystyle \textstyle \theta \approx 0,500} ,$ och frågar hur troligt det är att se 49 581 pojkar i 98 451 födslar.
Under $\textstyle H_{1}$ väljer vi $\textstyle \theta$ slumpmässigt från var som helst inom 0 till 1, och ställer samma fråga.

De flesta möjliga värden för $\textstyle \theta$ under $\textstyle H_{1}$ stöds mycket dåligt av observationerna. I huvudsak är den uppenbara oenigheten mellan metoderna inte en oenighet alls, utan snarare två olika påståenden om hur hypoteserna relaterar till data:

Frekventisten finner att $\textstyle H_{0}$ är en dålig förklaring till observationen.
Bayesianen finner att $\textstyle H_{0}$ är en mycket bättre förklaring för observationen än $\textstyle H_{1}$ .

Förhållandet mellan kön hos nyfödda är osannolikt 50/50 man/hona, enligt frekventisttestet. Ändå är 50/50 en bättre uppskattning än de flesta, men inte alla , andra förhållanden. Hypotesen $\textstyle \theta \approx 0,504$ skulle ha passat observationen mycket bättre än nästan alla andra förhållanden, inklusive $\textstyle \theta \approx 0,500$ .

Till exempel innebär detta val av hypoteser och tidigare sannolikheter påståendet: "om $\textstyle \theta$ > 0,49 och $\textstyle \theta$ < 0,51, då den tidigare sannolikheten för $\ att theta$ är exakt 0,5 är 0,50/0,51 $\approx$ 98 %." Givet en så stark preferens för ${\displaystyle \theta =0,5} ,$ är det lätt att se varför den bayesianska metoden gynnar $H_{0}$ inför $x\approx 0,5036$ , även om det observerade värdet för $x$ ligger $2,28\sigma$ från 0,5. Avvikelsen på över 2 sigma från $H_{0}$ anses signifikant i det frekventistiska tillvägagångssättet, men dess betydelse åsidosätts av priorn i det Bayesianska tillvägagångssättet.

Om vi tittar på det på ett annat sätt kan vi se att den tidigare fördelningen är i huvudsak platt med en deltafunktion vid $\textstyle \theta =0,5$ . Det är klart att detta är tveksamt. Faktum är att om du skulle föreställa reella tal som kontinuerliga, så skulle det vara mer logiskt att anta att det skulle vara omöjligt för ett givet tal att vara exakt parametervärdet, dvs. vi bör anta P $\ displaystyle P(\theta =0.5)=0}$ .

En mer realistisk fördelning för $\textstyle \theta$ i den alternativa hypotesen ger ett mindre överraskande resultat för den bakre delen av $\textstyle H_{0}$ . Om vi till exempel ersätter $\textstyle H_{1}$ med $\textstyle H_{2}:\theta =x$ , dvs. den maximala sannolikhetsuppskattningen för $\textstyle \theta$ , den bakre sannolikheten för $\textstyle H_{0}$ skulle bara vara 0,07 jämfört med 0,93 för $\textstyle H_{2}$ (Naturligtvis kan man faktiskt inte använda MLE som en del av en tidigare distribution).