Legendres sats om sfäriska trianglar

Inom geometri anges Legendres sats om sfäriska trianglar , uppkallad efter Adrien-Marie Legendre , enligt följande:

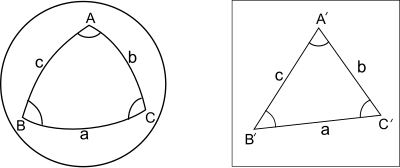
Låt ABC vara en sfärisk triangel på enhetssfären med små sidor a , b , c . Låt A'B'C' vara den plana triangeln med samma sidor. Då överskrider den sfäriska triangelns vinklar motsvarande vinklar i den plana triangeln med ungefär en tredjedel av det sfäriska överskottet (det sfäriska överskottet är det belopp med vilket summan av de tre vinklarna överstiger π ).

Satsen var mycket viktig för att förenkla det tunga numeriska arbetet med att beräkna resultaten av traditionella (pre-GPS och pre-dator) geodetiska undersökningar från omkring 1800 fram till mitten av 1900-talet.

Satsen angavs av Legendre (1787) som gav ett bevis (1798) i ett tillägg till rapporten om mätningen av den franska meridionalbågen som användes i definitionen av mätaren ( Delambre 1798 ) skördefel . Legendre hävdar inte att han var upphovsmannen till satsen trots tillskrivningen till honom. Tropfke (1903) hävdar att metoden var allmänt använd av lantmätare vid den tiden och kan ha använts så tidigt som 1740 av La Condamine för beräkning av den peruanska meridionalbågen .

Girards sats säger att det sfäriska överskottet av en triangel, E , är lika med dess area, Δ, och därför kan Legendres sats skrivas som

${\begin{aligned}AA'\;\approx \;BB' \;\approx \;CC'\;\approx \;{\frac {1}{3}}E\;=\;{\frac {1}{3}}\Delta ,\qquad a,\;b ,\;c\,\ll \,1.\end{aligned}}$

Överskottet, eller arean, av små trianglar är mycket liten. Betrakta till exempel en liksidig sfärisk triangel med sidor på 60 km på en sfärisk jord med en radie på 6371 km; sidan motsvarar ett vinkelavstånd på 60/6371=.0094, eller ungefär 10 ⁻² radianer (med en vinkel på 0,57° i mitten). Arean av en sådan liten triangel är väl approximerad av arean för en plan liksidig triangel med samma sidor: 1 ⁄ 2 a ² sin( π /3) = 0,0000433 radianer motsvarande 8,9″.

När sidorna på trianglarna överstiger 180 km, för vilka överskottet är cirka 80″, måste förhållandet mellan områdena och vinklarnas skillnader korrigeras med termer av fjärde ordningen i sidorna, som inte uppgår till mer än 0,01″:

${\begin{aligned}\Delta &=\Delta '\left(1+{\frac {a^{2}+b^{2}+c^{2}}{24}}\right) ,\\A&=A'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left(-2a^{2}+b^{2}+c^{ 2}\right),\\B&=B'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}-2b^ {2}+c^{2}}\right),\\C&=C'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}+b^{2}-2c^{2}}\right).\end{aligned}}$

(Δ′ är arean av den plana triangeln.) Detta resultat bevisades av Buzengeiger (1818) — ett utökat bevis kan hittas i Osborne (2013) (Appendix D13). Övriga resultat kartläggs av Nádeník (2004) .

Satsen kan utökas till ellipsoiden om a , b , c beräknas genom att dividera de sanna längderna med kvadratroten av produkten av de huvudsakliga krökningsradierna (se Osborne (2013) kapitel 5) vid hörnens medianlatitud (i stället för en sfärisk radie). Gauss (1828 , art. 26–28) gav mer exakta formler.

• Buzengeiger, Karl Heribert Ignatz (1818), "Vergleichung zweier kleiner Dreiecke von gleichen Seiten, wovon das eine sphärisch, das andere eben ist" , Zeitschrift für Astronomie und verwandte Wissenschaften , 6 : 264–270
• Clarke, Alexander Ross (1880), Geodesy , Clarendon Press. Återutgiven på Forgotten Books . {{ citation }} : Extern länk i |postscript= ( hjälp ) CS1 underhåll: postscript ( länk )
• Gauss, CF (1902) [1828]. Allmänna undersökningar av krökta ytor 1827 och 1825 . Princeton Univ. Lib. Engelsk översättning av Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828). {{ citera bok }} : Extern länk i |postscript= ( hjälp ) CS1 underhåll: postscript ( länk )
• Legendre, Adrien-Marie (1787), Mémoire sur les opérations trigonométriques, dont les résultats dépendant de la figure de la Terre , Artikel VI [1] , sid. 7 {{ citation }} : Extern länk i |others= ( hjälp )
• Legendre, Adrien-Marie (1798), Méthode pour déterminer la longueur exacte du quart du méridien d'après les observations faites pour la mesure de l'arc compris entre Dunkerque et Barcelone , s. 12–14 (Not III [2] )
• Nádeník, Zbynek (2004), Legendre theorem on sfäriska trianglar (PDF) , arkiverad från originalet (PDF) 2014-01-16
• Osborne, Peter (2013), The Mercator Projections , arkiverad från originalet 2013-09-24
• Tropfke, Johannes (1903), Geschichte der Elementar-Mathematik (Volym 2). , Verlag von Veit, sid. 295