Landau–Squire jet

Inom vätskedynamik beskriver Landau-Squire jet eller Submerged Landau jet en rund nedsänkt jet som utges från en punktkälla av momentum till ett oändligt flytande medium av samma sort . Detta är en exakt lösning på den inkompressibla formen av Navier-Stokes-ekvationerna, som först upptäcktes av Lev Landau 1944 och senare av Herbert Squire 1951. Den självliknande ekvationen härleddes faktiskt först av NA Slezkin 1934, men aldrig applicerat på jetplanen. Efter Landaus arbete fick VI Yatseyev den allmänna lösningen av ekvationen 1950.

Matematisk beskrivning

Landau-Squire jet strömlinjeformar för c=0,01

Landau-Squire jetströmlinjer för c=0,1

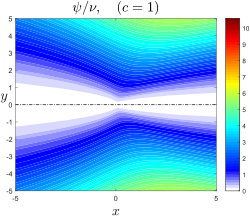
Landau-Squire jet strömlinjeformar för c=1

Problemet beskrivs i sfäriska koordinater $(r,\theta ,\phi )$ med hastighetskomponenter $(u,v,0)$ . Flödet är axelsymmetriskt, dvs oberoende av $\phi$ . Sedan minskar kontinuitetsekvationen och de inkompressibla Navier–Stokes-ekvationerna till

{\begin{aligned}&{\frac {1}{r^{2}} }{\frac {\partial }{\partial r}}(r^{2}u)+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta } }(v\sin \theta )=0\\[8pt]&u{\frac {\partial u}{\partial r}}+{\frac {v}{r}}{\frac {\partial u}{ \partial \theta }}-{\frac {v^{2}}{r}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}+\ nu \left(\nabla ^{2}u-{\frac {2u}{r^{2}}}-{\frac {2}{r^{2}}}{\frac {\partial v}{ \partial \theta }}-{\frac {2v\cot \theta }{r^{2}}}\right)\\[8pt]&u{\frac {\partial v}{\partial r}}+{ \frac {v}{r}}{\frac {\partial v}{\partial \theta }}+{\frac {uv}{r}}=-{\frac {1}{\rho r}}{ \frac {\partial p}{\partial \theta }}+\nu \left(\nabla ^{2}v+{\frac {2}{r^{2}}}{\frac {\partial u}{ \partial \theta }}-{\frac {v}{r^{2}\sin ^{2}\theta }}\right)\end{aligned}}

var

\nabla ^{2}={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\ partiell }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \ theta {\frac {\partial }{\partial \theta }}\right).

En liknande beskrivning finns tillgänglig för lösningen i följande formulär,

u={\frac {\nu }{r\sin \theta }}f'(\theta ),\quad v=-{\frac {\nu }{r\sin \theta }}f(\ theta ).

Genom att ersätta ovanstående självliknande form i de styrande ekvationerna och använda randvillkoren $u=v=p-p_{\infty }=0$ i oändligheten, hittar man formen för tryck som

{\frac {p-p_{\infty }}{\rho }}=-{\frac {v^{2} }{2}}+{\frac {\nu u}{r}}+{\frac {c_{1}}{r^{2}}}

där $c_{1}$ är en konstant. Med hjälp av detta tryck finner vi igen från momentumekvationen,

-{\frac {u^{2}}{r}}+{\frac {v}{r}}{\frac {\partial u}{\partial \theta }}={\frac {\ nu }{r^{2}}}\left[2u+{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\ frac {\partial u}{\partial \theta }}\right)\right]+{\frac {2c_{1}}{r^{3}}}.

Genom att ersätta $\theta$ med $\mu =\cos \theta$ som oberoende variabel, blir hastigheterna

u=-{\frac {\nu }{r}}f'(\mu),\quad v=-{\frac {\nu }{r}}{\frac {f(\mu )}{\sqrt {1-\mu ^{2}}}}

(för korthetens skull används samma symbol för $f(\theta )$ och $f(\mu )$ även om de är funktionellt lika, men har olika numeriska värden ) och ekvationen blir

f'^{2}+ff''=2f'+[(1-\mu ^{2})f'']'-2c_{1}.

Efter två integrationer minskar ekvationen till

f^{2}=4\mu f+2(1- \mu ^{2})f'-2(c_{1}\mu ^{2}+c_{2}\mu +c_{3}),

där $c_{2}$ och $c_{3}$ är integrationskonstanter. Ovanstående ekvation är en Riccati-ekvation . Efter en viss beräkning kan den allmänna lösningen visa sig vara

f=\alpha (1+\mu )+\beta (1-\mu )+{\frac {2(1-\mu ^{2})(1+\mu )^{\beta }}{(1-\mu )^{\alpha }}}\left[c-\int _{1}^{\mu }{\frac {(1+\mu )^{\ beta }}{(1-\mu )^{\alpha }}}\right]^{-1},

där $\alpha ,\ \beta ,\ c$ är konstanter. Den fysiskt relevanta lösningen för strålen motsvarar fallet $\alpha =\beta =0$ (På motsvarande sätt säger vi att $c_{1}=c_ {2}=c_{3}=0$ , så att lösningen är fri från singulariteter på symmetriaxeln, förutom vid origo). Därför,

f={\frac {2(1-\mu ^{2})}{c+1-\mu }}={\frac {2\sin ^{2}\theta }{c+1- \cos \theta }}.

Funktionen $f$ är relaterad till streamfunktionen som $\psi =\nu rf$ , alltså konturer av $f$ för olika värden på $c$ ger effektiviseringarna. Konstanten $c$ beskriver kraften vid origo som verkar i strålens riktning (denna kraft är lika med hastigheten för rörelsemängdsöverföring över vilken sfär som helst runt origo plus kraften i jetriktningen som utövas av sfären pga. till tryck och viskösa krafter) ges det exakta förhållandet mellan kraften och konstanten av

{\frac {F}{2\pi \rho \nu ^{2}}}={\frac {32(c+1)}{3c(c+2)}}+8(c+1 )-4(c+1)^{2}\ln {\frac {c+2}{c}}.

Lösningen beskriver en vätskestråle som snabbt rör sig bort från ursprunget och drar med sig den långsamt rörliga vätskan utanför strålen. Strålens kant kan definieras som den plats där strömlinjerna är på minsta avstånd från axeln, dvs kanten ges av