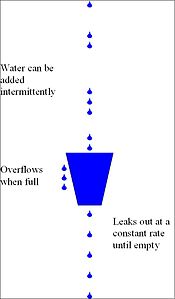
Läckande hink
Den läckande hinken är en algoritm baserad på en analogi av hur en hink med en konstant läcka kommer att svämma över om antingen den genomsnittliga hastigheten med vilken vatten hälls in överstiger den hastighet med vilken hinken läcker eller om mer vatten än hinkens kapacitet är hällde i allt på en gång. Den kan användas för att bestämma om någon sekvens av diskreta händelser överensstämmer med definierade gränser för deras medel- och topphastigheter eller frekvenser, t.ex. för att begränsa de åtgärder som är associerade med dessa händelser till dessa takter eller fördröja dem tills de överensstämmer med hastigheterna. Den kan också användas för att kontrollera överensstämmelse eller begränsa till enbart en genomsnittlig frekvens, dvs. ta bort alla variationer från genomsnittet.
Det används i paketkopplade datornätverk och telekommunikationsnätverk i både trafikpolisering , trafikutformning och schemaläggning av dataöverföringar , i form av paket , till definierade gränser för bandbredd och burstiness (ett mått på variationerna i trafikflödet ) .
En version av den läckande hinken, den generiska cellhastighetsalgoritmen , rekommenderas för ATM-nätverk ( Asynchronous Transfer Mode ) i användnings-/nätverksparameterkontroll vid användar-nätverksgränssnitt eller internätverksgränssnitt eller nätverk-till-nätverk-gränssnitt för att skydda ett nätverk från alltför höga trafiknivåer på anslutningar som dirigeras genom den. Den generiska cellhastighetsalgoritmen, eller en ekvivalent, kan också användas för att forma överföringar av ett nätverksgränssnittskort till ett ATM-nätverk.
Åtminstone vissa implementeringar av den läckande hinken är en spegelbild av token-bucketalgoritmen och kommer, givet ekvivalenta parametrar, att bestämma exakt samma sekvens av händelser för att överensstämma med eller inte överensstämma med samma gränser.
Översikt
Två olika metoder för att tillämpa denna läckande hinkanalogi beskrivs i litteraturen. Dessa ger vad som verkar vara två olika algoritmer, som båda kallas leaky bucket-algoritmen och i allmänhet utan hänvisning till den andra metoden. Detta har resulterat i förvirring om vad den läckande hinkalgoritmen är och vad dess egenskaper är.
I en version är hinken en räknare eller variabel skild från trafikflödet eller schemat för händelser. Denna räknare används endast för att kontrollera att trafiken eller händelserna överensstämmer med gränserna: Räknaren inkrementeras när varje paket anländer till den punkt där kontrollen görs eller en händelse inträffar, vilket motsvarar hur vatten tillsätts intermittent till hinken. Räknaren dekrementeras också med en fast hastighet, motsvarande hur vattnet läcker ut ur hinken. Som ett resultat representerar värdet i räknaren nivån på vattnet i hinken. Om räknaren förblir under ett specificerat gränsvärde när ett paket anländer eller en händelse inträffar, dvs. hinken svämmar inte över, indikerar det dess överensstämmelse med bandbredds- och burstiness-gränserna eller medel- och topphastighetshändelsegränserna. Denna version kallas här den läckande skopan som en mätare .
I den andra versionen är hinken en kö i trafikflödet. Denna kö används för att direkt styra det flödet: Paket läggs in i kön när de anländer, motsvarande vattnet som läggs till hinken. Dessa paket tas sedan bort från kön ( först till kvarn, först till kvarn ), vanligtvis till en fast hastighet, t.ex. för vidare överföring, motsvarande vatten som läcker från hinken. Denna konfiguration påtvingar överensstämmelse snarare än att kontrollera den, och där utgången betjänas med en fast hastighet (och där paketen alla är lika långa), är den resulterande trafikströmmen nödvändigtvis fri från burstiness eller jitter. Så i den här versionen är själva trafiken analogen till vattnet som passerar genom hinken. Denna version kallas här leaky bucket som en kö .
Den läckande hinken som en mätare är exakt likvärdig med (en spegelbild av) token-bucket- algoritmen, dvs. processen att tillsätta vatten till den läckande hinken speglar exakt den för att ta bort tokens från token-hinken när ett överensstämmande paket anländer, processen med läckage av vatten från den läckande hinken speglar exakt det att regelbundet lägga till tokens till token-hinken, och testet att den läckande hinken inte kommer att svämma över är en spegel av testet att token-hinken innehåller tillräckligt med polletter och inte kommer att "rinna under". Givet motsvarande parametrar kommer de två algoritmerna att se samma trafik som överensstämmande eller icke-överensstämmande. Den läckande hinken som kö kan ses som ett specialfall av den läckande hinken som en mätare.
Som en mätare
Jonathan S. Turner tillskrivs den ursprungliga beskrivningen av algoritmen för läckande hink och beskriver den på följande sätt: "En räknare som är associerad med varje användare som sänder på en anslutning inkrementeras närhelst användaren skickar ett paket och minskas med jämna mellanrum. Om räknaren överstiger en tröskel vid inkrementering kasserar nätverket paketet. Användaren specificerar hastigheten med vilken räknaren minskas (detta bestämmer den genomsnittliga bandbredden) och värdet på tröskeln (ett mått på burstiness)". Hinken (analog med räknaren) används i detta fall som en mätare för att testa paketens överensstämmelse, snarare än som en kö för att direkt kontrollera dem.
En annan beskrivning av vad som i huvudsak är samma mätarversion av algoritmen, den generiska cellhastighetsalgoritmen , ges av ITU-T i rekommendation I.371 och i ATM-forumets UNI-specifikation. Beskrivningen, där termen cell är ekvivalent med paket i Turners beskrivning ges av ITU-T enligt följande: "The continuous-state leaky bucket kan ses som en ändlig kapacitetshink vars verkliga innehåll rinner ut vid en kontinuerlig hastighet på 1 innehållsenhet per tidsenhet och vars innehåll ökas med inkrementet T för varje överensstämmande cell... Om innehållet i hinken vid en cellankomst är mindre än eller lika med gränsvärdet τ , är cellen överensstämmer; annars är cellen icke-överensstämmande. Skopans kapacitet (räknarens övre gräns) är ( T + τ )". Dessa specifikationer anger också att, på grund av dess ändliga kapacitet, om innehållet i skopan vid den tidpunkt då överensstämmelsen testas är större än gränsvärdet och följaktligen cellen inte överensstämmer, så lämnas skopan oförändrad; det vill säga att vattnet helt enkelt inte tillsätts om det skulle få hinken att svämma över.
David E. McDysan och Darrel L. Spohn ger en kommentar till beskrivningen från ITU-T/ATM Forum. I detta anger de "I analogin med den läckande hinken flyter [ATM]-cellerna faktiskt inte genom hinken, det är bara kontrollen för överensstämmelse med antagning som gör det". Men, ovanligt i beskrivningarna i litteraturen, hänvisar McDysan och Spohn också till algoritmen för läckande hink som en kö, som fortsätter "Notera att en implementering av trafikformning är att faktiskt få cellerna att flöda genom hinken".
När de beskriver hur ITU-T:s version av algoritmen fungerar, åberopar McDysan och Spohn en "uppfattning som vanligtvis används i köteorin om en fiktiv "gremlin". Denna gremlin inspekterar nivån i hinken och vidtar åtgärder om nivån är över gränsvärdet τ : vid polisarbete (figur 2) öppnar den en lucka, vilket gör att det ankommande paketet tappas och hindrar dess vatten från att komma in i hink; i formning (figur 3), trycker den upp en klaff, vilket fördröjer det ankommande paketet och hindrar det från att leverera sitt vatten, tills vattennivån i hinken faller under τ .
Skillnaden mellan beskrivningarna som ges av Turner och ITU-T/ATM-forumet är att Turners är specifik för trafikpolisen , medan ITU-T/ATM-forumet är tillämpligt på både trafikpolisering och trafikformning. Turner anger inte heller att innehållet i räknaren endast ska påverkas av överensstämmande paket, och bör endast ökas när detta inte skulle få det att överskrida en gräns, dvs Turner anger inte uttryckligen att hinkens kapacitet eller räknarens maxvärde är ändlig. För att göra Turners beskrivning tydligt anpassad till ITU-T, måste påståendet "Om räknaren överskrider ett tröskelvärde vid inkrementering, kastar nätverket paketet" ändras till något i stil med "Om räknaren skulle överskrida ett tröskelvärde [motsvarande hinkdjup, T + τ , i ITU-T-beskrivningen] när det inkrementeras, kasserar nätverket paketet och räknaren inkrementeras inte", dvs den inkrementeras endast när den är mindre än eller lika med gränsvärdet, τ , eller åtminstone T mindre än skopdjupet i ITU-T-beskrivningen.
Även om beskrivningen som ges av Turner inte anger att räknaren endast ska påverkas av överensstämmande paket, ges den i termer av en trafikpolisfunktion, där övernitiskhet att begränsa en anslutning som innehåller icke-överensstämmande paket kanske inte är ett problem. I vissa sammanhang, såsom med variabel bithastighet (VBR), kan förlusten av vilket paket som helst förstöra hela ett meddelande med högre lager, t.ex. en OSI Network Layer PDU. Om du i så fall kasserar alla följande paket av den skadade PDU:n förlorar du en onödig nätverksbelastning. Det skulle dock vara helt oacceptabelt i trafikformning för ett paket som inte klarar överensstämmelsetestet att påverka hur lång tid innan överensstämmelse kan inträffa nästa gång, dvs. om handlingen att testa ett efterföljande paket för överensstämmelse skulle ändra hur länge ett paket som för närvarande väntar på att överensstämma har att vänta. Detta är exakt vad som skulle hända om vattnet från paket som inte överensstämmer skulle läggas till hinken, eftersom alla efterföljande paket som inte överensstämmer skulle höja vattennivån och därmed få ett paket som väntar på att överensstämma att vänta längre.
Varken Turner eller ITU-T tar upp frågan om paket med variabel längd. Beskrivningen enligt ITU-T är dock för ATM-celler, som är paket med fast längd, och Turner utesluter inte specifikt paket med variabel längd. Därför, i båda fallen, om mängden med vilken hinkinnehållet eller räknaren inkrementeras för ett överensstämmande paket är proportionell mot paketets längd, kommer de både att ta hänsyn till längden och tillåta algoritmen att begränsa bandbredden för trafiken uttryckligen snarare än begränsa pakethastigheten. Till exempel skulle kortare paket lägga till mindre till hinken, och skulle därmed kunna anlända med mindre intervall; medan längre paket skulle lägga till mer och därför måste separeras med proportionellt större intervall för att anpassa sig.
Begreppet drift
En beskrivning av konceptet för driften av den läckande skopans algoritm som en mätare som kan användas i antingen trafikpolis eller trafikformning kan anges enligt följande:
- En hink med fast kapacitet, associerad med varje virtuell anslutning eller användare, läcker med en fast hastighet.
- Om hinken är tom slutar den att läcka.
- För att ett paket ska överensstämma måste det vara möjligt att lägga till en specifik mängd vatten till hinken: Den specifika mängden som tillsätts av ett överensstämmande paket kan vara samma för alla paket eller kan vara proportionell mot paketets längd.
- Om denna mängd vatten skulle få hinken att överskrida sin kapacitet så överensstämmer inte paketet och vattnet i hinken lämnas oförändrat.
Används
Den läckande skopan som mätare kan användas i antingen trafikformning eller trafikpolisering . Till exempel, i ATM-nätverk, i form av den generiska cellhastighetsalgoritmen, används den för att jämföra bandbredden och burstiness för trafik på en Virtual Channel (VC) eller Virtual Path (VP) mot de specificerade gränserna för hastigheten med vilken celler kan anlända och maximalt jitter, eller variation i inter-ankomstintervall, för VC eller VP. Inom trafikpolisen kan celler som inte överensstämmer med dessa gränser (icke-överensstämmande celler) kasseras (släppas) eller kan reduceras i prioritet (för att nedströms trafikledningsfunktioner ska minska om det är trängsel). I trafikformning fördröjs celler tills de överensstämmer. Trafikpolisering och trafikformning används ofta i UPC/NPC för att skydda nätverket mot överdriven eller överdrivet sprängtrafik, se bandbreddshantering och undvikande av trängsel . Trafikformning används vanligtvis i nätverksgränssnitten i värdar för att förhindra att överföringar överskrider bandbredds- eller jittergränserna och förkastas av trafikhanteringsfunktioner i nätverket. (Se schemaläggning (beräkning) och nätverksschemaläggare .)
Algoritmen för läckande hink som mätare kan också användas i en läckande hinkräknare för att mäta frekvensen av slumpmässiga eller stokastiska processer . En läckande hinkräknare kan användas för att upptäcka när medel- eller toppfrekvensen av händelser ökar över en acceptabel bakgrundsnivå, dvs när skopan svämmar över. Händelser som inte orsakar översvämning, dvs har tillräckligt låga hastigheter och är väl fördelade över tiden, kan dock ignoreras. Till exempel kan en sådan läckande hinkräknare användas för att upptäcka när det finns en plötslig skur av korrigerbara minnesfel eller när det har skett en gradvis, men betydande, ökning av den genomsnittliga frekvensen, vilket kan indikera ett förestående fel, etc.
Användningen av leaky bucket-algoritmen i en leaky bucket-räknare liknar den i trafikledning, genom att den används som en mätare. I huvudsak ersätter händelserna paketen i beskrivningen, där varje händelse gör att en mängd vatten läggs till hinken. Om hinken skulle svämma över, som ett resultat av händelsen, bör händelsen utlösa åtgärden associerad med en out-of-limit-händelse. Vissa implementeringar tycks vara parallella med Turners beskrivning, eftersom det inte finns någon uttrycklig gräns för det maximala värdet som räknaren kan ta, vilket innebär att när räknaren väl har överskridit tröskeln, kan den inte återgå till sitt tidigare tillstånd förrän en period som är betydligt större än motsvarigheten till utsläppsintervallet har passerat, vilket kan ökas med vad som annars skulle vara överensstämmande händelser. Andra implementeringar kanske inte ökar räknaren medan den flödar över, vilket gör att den korrekt kan avgöra om följande händelser överensstämmer eller inte.
Parametrar
I fallet med den läckande hinkalgoritmen som en mätare, kan gränserna för trafiken vara bandbredd och en burstiness av utgången.
Bandbreddsgränsen och burstinessgränsen för anslutningen kan anges i ett trafikavtal . En bandbreddsgräns kan anges som ett paket- eller bildrutehastighet, en byte eller bithastighet eller som ett emissionsintervall mellan paketen. En gräns för burstiness kan specificeras som en jitter eller fördröjningsvariation , eller som en maximal skurstorlek (MBS).
Flera uppsättningar kontraktsparametrar kan appliceras samtidigt på en anslutning med hjälp av flera instanser av den läckande hinkalgoritmen, som var och en kan ta en bandbredd och en burstiness-gräns: se Generisk cellhastighetsalgoritm § Dual Leaky Bucket Controller .
Emissionsintervall
Hastigheten med vilken skopan läcker kommer att bestämma bandbreddsgränsen, som kallas medelhastigheten av Turner och vars omvända hänvisas till som emissionsintervallet av ITU-T. Det är lättast att förklara vad detta intervall är där paket har en fast längd. Därför antar den första delen av denna beskrivning detta, och implikationerna av variabla paketlängder betraktas separat.
Tänk på en hink som är exakt fylld till toppen av föregående trafik, dvs. när den maximalt tillåtna burstiness redan har inträffat, dvs. det maximala antalet paket eller celler har precis anlänt inom den minsta tid för att de fortfarande ska överensstämma med bandbredden och jittergränser. Minsta intervall innan nästa paket kan överensstämma är då den tid det tar för hinken att läcka exakt den mängd vatten som levereras av ett paket, och om ett paket testas och överensstämmer vid den tidpunkten kommer detta att fylla hinken exakt en gång till . Så snart hinken är fylld, är den maximala hastigheten som paket kan överensstämma med detta intervall mellan varje paket.
Turner hänvisar till denna hastighet som medelvärdet, vilket antyder att dess invers är medelintervallet. Det finns dock en viss oklarhet i vad den genomsnittliga hastigheten och intervallet är. Eftersom paket kan komma fram med vilken lägre hastighet som helst, är detta en övre gräns, snarare än ett fast värde, så det kan i bästa fall kallas maximivärdet för medelhastigheten. Dessutom, under den tid den maximala burstinessen inträffar, kan paket anlända med mindre intervall och därmed med en högre hastighet än detta. Så, för vilken period som helst mindre än oändligheten, kan den faktiska genomsnittliga hastigheten vara (men är inte nödvändigtvis) större än detta och medelintervallet kan vara (men är inte nödvändigtvis) mindre än emissionsintervallet. Därför, på grund av denna tvetydighet, används termen emissionsintervall härefter. Det är dock fortfarande sant att det lägsta värdet som det långa medelintervallet kan ta tenderar att vara emissionsintervallet.
För paket med variabel längd, där mängden som läggs till hinken är proportionell mot paketets längd, varierar den maximala hastigheten med vilken de kan anpassa sig beroende på deras längd: mängden som hinken måste ha läckt från full för att ett paket ska överensstämma är mängden paketet kommer att lägga till, och om detta är proportionellt mot paketets längd, så är intervallet mellan det och det föregående paketet som fyllde hinken. Därför är det inte möjligt att specificera ett specifikt emissionsintervall för paket med variabel längd, och bandbreddsgränsen måste specificeras explicit, i bitar eller byte per sekund.
Fördröjningsvariationstolerans
Det är lättast att förklara vad denna tolerans är där paket har en fast längd. Därför antar den första delen av denna beskrivning detta, och implikationerna av variabla paketlängder betraktas separat.
ITU-T definierar ett gränsvärde, τ , som är mindre än hinkens kapacitet med T (den mängd med vilken hinkinnehållet ökas för varje överensstämmande cell), så att hinkens kapacitet är T + τ . Detta gränsvärde anger hur mycket tidigare ett paket kan anlända än vad det normalt skulle förväntas om paketen anlände med exakt emissionsintervallet mellan dem.
Föreställ dig följande situation: En hink läcker med 1 enhet vatten per sekund, så gränsvärdet, τ och mängden vatten som tillförs av ett paket, T , är i praktiken i sekunder. Denna hink börjar tom, så när ett paket anländer till hinken, fyller den inte riktigt hinken genom att tillsätta dess vatten T , och hinken är nu τ under sin kapacitet. Så när nästa paket anländer behöver hinken bara ha tömts med T – τ för att detta ska överensstämma. Så intervallet mellan dessa två paket kan vara så mycket som τ mindre än T .
Detta sträcker sig till flera paket i en sekvens: Föreställ dig följande: hinken börjar återigen tom, så det första paketet som kommer måste överensstämma. Hinken blir sedan exakt full efter att ett antal överensstämmande paket, N , har anlänt på minsta möjliga tid för att de ska överensstämma. För att det sista ( N: te) paketet ska överensstämma måste hinken ha läckt tillräckligt med vatten från de föregående N – 1 paketen (( N – 1) * T sekunders värde) för att det ska vara exakt vid gränsvärdet τ just nu. Därför är vattnet som läcker ( N – 1) T – τ , vilket eftersom läckan är en enhet per sekund tog exakt ( N – 1) T – τ sekunder att läcka. Den kortaste tiden under vilken alla N paket kan anlända och anpassa sig är alltså ( N – 1) T – τ sekunder, vilket är exakt τ mindre än den tid det skulle ha tagit om paketen hade anlänt vid exakt emissionsintervallet.
Paket kan dock bara anlända med intervaller mindre än T där hinken inte fylls av det föregående paketet. Om så är fallet måste hinken ha tömts hela mängden T innan nästa paket överensstämmer. Så när väl denna tolerans har använts av paket som anländer vid mindre än T måste efterföljande ramar anlända med intervall som inte är mindre än T . De kan dock komma med längre intervall, när hinken inte kommer att fyllas av dem. När detta har hänt kan paket återigen anlända med intervaller mindre än T tills toleransen återigen är förbrukad. Men eftersom hinken slutar läcka när den är tom, finns det alltid en gräns ( τ ) för hur mycket tolerans som kan samlas på dessa intervall större än T , men mycket större än T kan de vara eller många av dem det finns.
Eftersom gränsvärdet τ definierar hur mycket tidigare ett paket kan anlända än vad som förväntas, är det gränsen för skillnaden mellan maximala och minimala fördröjningar från källan till den punkt där överensstämmelsetestet görs (förutsatt att paketen genereras utan jitter). Därför används termen Cell Delay Variation Tolerance (CDVt) för denna parameter i ATM.
Som ett exempel är en möjlig källa till fördröjningsvariation där ett antal anslutningar (strömmar av paket) multiplexeras tillsammans vid utgången av en switch. Om man antar att summan av bandbredderna för dessa anslutningar är mindre än utgången, kan alla paket som anländer sändas så småningom. Men om deras ankomster är oberoende, t.ex. för att de kommer till olika ingångar på växeln, kan flera anlända vid eller nästan samtidigt. Eftersom utgången bara kan sända ett paket åt gången måste de andra köa i en buffert tills det är deras tur att sändas. Denna buffert introducerar sedan en ytterligare fördröjning mellan ett paket som anländer till en ingång och sänds av utgången, och denna fördröjning varierar beroende på hur många andra paket som redan står i kö i bufferten. En liknande situation kan uppstå vid utgången av en värd (i NIC) när flera paket har samma eller liknande utgivningstider, och denna fördröjning kan vanligtvis modelleras som en fördröjning i en virtuell utmatningsbuffert.
För paket med variabel längd, där mängden vatten som tillsätts av ett givet paket är proportionell mot dess längd, kan τ inte ses som en gräns för hur full hinken kan vara när ett paket anländer, eftersom detta varierar beroende på paketets storlek . Men den tid det tar att tömma från denna nivå till att tömma är fortfarande hur mycket tidigare ett paket kan anlända än vad som förväntas, när paket sänds vid bandbreddsgränsen. Det är således fortfarande den maximala variationen i överföringsfördröjning till den punkt där överensstämmelsetestet tillämpas som kan tolereras, och därmed toleransen för maximal fördröjningsvariation.
Maximal burststorlek
Gränsvärdet eller fördröjningsvariationstoleransen styr också hur många paket som kan anlända i en skur, bestämt av det överskjutande djupet på hinken över den kapacitet som krävs för ett enstaka paket. Därför är MBS också ett mått på burstiness eller jitter, och det är möjligt att specificera burstiness som en MBS och härleda gränsvärdet τ från detta eller att specificera det som en jitter/fördröjningsvariationstolerans/gränsvärde, och härleda MBS från detta.
En skur eller klump av paket kan komma fram med en högre hastighet än vad som bestäms av emissionsintervallet T . Detta kan vara linjehastigheten för den fysiska skiktanslutningen när paketen i skuren kommer rygg-mot-rygg. Men som i ATM kan toleransen tillämpas på en lägre hastighet, i så fall kan den hållbara cellhastigheten (SCR) och paketskuren (celler) komma till en högre hastighet, men mindre än linjehastigheten för fysiskt skikt, i så fall Peak Cell Rate (PCR). MBS kan då vara antalet celler som behövs för att transportera ett högre lagerpaket (se segmentering och återmontering ), där paketen sänds med en maximal bandbredd som bestäms av SCR och celler i paketen sänds vid PCR; sålunda tillåta den sista cellen i paketet, och själva paketet, att anlända betydligt tidigare än vad det skulle göra om cellerna skickades vid SCR: överföringsvaraktighet = (MBS-1)/PCR snarare än (MBS-1)/SCR. Denna sprängning vid PCR:n lägger en signifikant högre belastning på delade resurser, t.ex. växlingsutgångsbuffertar, än överföring vid SCR:n, och är sålunda mer sannolikt att resultera i buffertspill och nätstockning. Emellertid lägger den en mindre belastning på dessa resurser än sändning vid SCR med ett gränsvärde, τ SCR , som tillåter MBS-celler att sändas och anlända back-to-back med linjehastigheten.
Om gränsvärdet är tillräckligt stort, kan flera paket anlända i en skur och fortfarande överensstämma: om hinken börjar från tom kommer det första paketet som kommer att lägga till T , men om innehållet är när nästa paket anländer under τ , kommer detta också att överensstämma. Om man antar att varje paket tar δ att komma fram, så om τ (uttryckt som den tid det tar för hinken att tömmas från gränsvärdet) är lika med eller större än emissionsintervallet minus den minsta mellantiden, T – δ , det andra paketet kommer att överensstämma även om den kommer som en skur med den första. På liknande sätt, om τ är lika med eller större än ( T – δ ) × 2, kan 3 paket anlända i en skur, etc.
Den maximala storleken på denna skur, M , kan beräknas från emissionsintervallet, T ; den maximala jittertoleransen, τ ; och tiden det tar att sända/ta emot ett paket, δ , enligt följande:
På samma sätt kan minimivärdet för jittertolerans τ som ger en specifik MBS beräknas från MBS enligt följande:
I fallet med ATM, där MBS tekniskt sett endast hänför sig till SCR-toleransen, i ovanstående ekvation är tiden det tar för varje paket att anlända, δ , emissionsintervallet för celler vid PCR T PCR , och emissionsintervallet, T , är emissionsintervallet för SCR T SCR . Där MBS ska vara antalet celler som krävs för att transportera ett segmenterat paket, bör gränsvärdet i ovanstående, τ , vara det för SCR τ SCR . Men vid UNI eller ett NNI, där celler vid PCR kommer att ha utsatts för fördröjningsvariationer, bör det vara gränsvärdet för SCR plus det för PCR τ SCR + τ PCR .
För paket med variabel längd kommer den maximala skurstorleken att bero på längden på paketen i skuren och det finns inget enskilt värde för den maximala skurstorleken. Det är emellertid möjligt att specificera den totala skurlängden i byte, från bytehastigheten för ingångsströmmen, den ekvivalenta bytehastigheten för läckan och hinkdjupet.
Jämförelse med token-bucket-algoritmen
Den läckande hinkalgoritmen kontrasteras ibland med token-bucketalgoritmen . Ovanstående funktionskoncept för den läckande skopan som en mätare kan dock direkt jämföras med algoritmen för tokenskopa, vars beskrivning ges i den artikeln som följande:
- En token läggs till hinken var 1/ r sekund.
- Skopan rymmer högst b polletter. Om en token kommer när hinken är full slängs den.
- Om färre än n token är tillgängliga, tas inga tokens bort från hinken, och paketet anses vara icke-konformt.
Detta kan jämföras med operationskonceptet, upprepat från ovan:
- En hink med fast kapacitet, associerad med varje virtuell anslutning eller användare, läcker med en fast hastighet.
- Om hinken är tom slutar den att läcka.
- För att ett paket ska överensstämma måste det vara möjligt att lägga till en specifik mängd vatten till hinken: Den specifika mängden som tillsätts av ett överensstämmande paket kan vara samma för alla paket, eller kan vara proportionell mot paketets längd.
- Om denna mängd vatten skulle få hinken att överskrida sin kapacitet så överensstämmer inte paketet och vattnet i hinken lämnas oförändrat.
Som kan ses är dessa två beskrivningar i huvudsak spegelbilder av varandra: man lägger till något i hinken regelbundet och tar bort något för att anpassa paket ner till en gräns på noll; den andra tar bort regelbundet och lägger till för att anpassa paket upp till en gräns för hinkens kapacitet. Så, är en implementering som lägger till tokens för ett överensstämmande paket och tar bort dem med en fast hastighet en implementering av den läckande hinken eller av token-hinken? På samma sätt, vilken algoritm används i en implementering som tar bort vatten för ett överensstämmande paket och tillsätter vatten med en fast hastighet? Båda är faktiskt desamma, dvs implementeringar av både den läckande hinken och token-hinken, eftersom dessa är samma grundläggande algoritm som beskrivs på olika sätt. Detta förklarar varför, givet motsvarande parametrar, de två algoritmerna kommer att se exakt samma paket som överensstämmande eller icke-överensstämmande. Skillnaderna i egenskaper och prestanda för implementeringar av algoritmerna för läckande och token-bucket beror alltså helt och hållet på skillnaderna i implementeringarna, dvs. de härrör inte från skillnader i de underliggande algoritmerna.
Punkterna att notera är att den läckande hinkalgoritmen, när den används som en mätare, kan tillåta en överensstämmande utdatapaketström med jitter eller burstiness, kan användas i trafikpolisering såväl som formning, och kan implementeras för paket med variabel längd.
Som en kö
Den läckande hinken som en kö är i huvudsak ett sätt att beskriva en enkel FIFO- buffert eller kö som servas med en fast hastighet för att ta bort burstiness eller jitter. En beskrivning av det ges av Andrew S. Tanenbaum , i (en äldre version av) hans bok Computer Networks som "Den läckande hinken består av en finit kö. När ett paket anländer, om det finns plats i kön läggs det till kön; annars slängs den. Vid varje klockmarkering sänds ett paket (om inte kön är tom)". En implementering av den läckande hinken som en kö är därför alltid en form av trafikformningsfunktion.
Som kan ses är denna implementering begränsad genom att paketen endast alltid sänds med en fast hastighet. För att understryka detta, säger Tanenbaum också att "Den läckande hinkalgoritmen framtvingar ett styvt utdatamönster vid den genomsnittliga hastigheten, oavsett hur sprängfylld [ingångs]trafiken är". Detta påstående är dock endast strikt sant så länge som kön inte blir tom: om den genomsnittliga ankomsthastigheten är mindre än takten för klockslag, eller om ingången är tillräckligt sprängfylld för att förlusterna bringar återstodens hastighet under clock tick rate (dvs luckor i ingångsströmmen är tillräckligt långa och kön är tillräckligt liten för att den kan bli tom), kommer det att finnas luckor i utströmmen.
En ytterligare begränsning är att den läckande hinken som en kötrafikformningsfunktion endast sänder paket på bockarna; därför, om den används inom ett nätverk, motsvarande UPC och NPC , ålägger den också en fast fas på den vidare överföringen av paket. När en läckande hinkmätare används för att kontrollera vidare överföring, sänds ett paket så snart det överensstämmer, dvs. i förhållande till det föregående eller, om det redan överensstämmer, dess ankomsttid. inte enligt någon godtycklig lokal klocka. Omvänt, i samband med överföringsfördröjningen, utgör denna påläggning av en fast fas som över tiden kan skilja sig från den för en i övrigt överensstämmande indatapaketström, en fördröjningsvariation och följaktligen ett jitter. Jitter orsakat på detta speciella sätt kunde endast observeras där fördröjningen mäts som transittiden mellan två separata mätpunkter, på vardera sidan av den läckande hinken som en köformningsfunktion. I samband med dataöverföringar i realtid är det dock denna fördröjning från slut till ände som bestämmer fördröjningen för mottagen data. Därför är den läckande hinken som kö olämplig för trafikformande realtidsöverföringar.
Att begränsa paket med variabel längd genom att använda algoritmen för läckande hink som en kö är betydligt mer komplicerat än för paket med fast längd. Tanenbaum ger en beskrivning av en "byte-counting" läckande hink för paket med variabel längd enligt följande: "Vid varje bock initieras en räknare till n. Om det första paketet i kön har färre byte än räknarens nuvarande värde, den sänds och räknaren minskas med det antalet byte. Ytterligare paket kan också skickas, så länge räknaren är tillräckligt hög. När räknaren sjunker under längden på nästa paket i kön, stoppas överföringen tills nästa bock, vid vilken tidpunkt restbyteantalet återställs [till n] och flödet kan fortsätta". Precis som med versionen för paket med fast längd har denna implementering en stark effekt på överföringsfasen, vilket resulterar i varierande fördröjningar från slut till ände och olämplighet för realtidstrafikformning.
Används
Den läckande hinken som en kö kan endast användas för att forma trafik till en specificerad bandbredd utan jitter i utgången. Det kan användas inom nätverket, t.ex. som en del av bandbreddshantering, men är mer lämpligt för trafikformning i värdarnas nätverksgränssnitt. Leaky bucket-algoritm används i Nginx ngx_http_limit_conn_module -modul för att begränsa antalet samtidiga anslutningar som kommer från en enda IP-adress .
Parametrar
I fallet med den läckande hinkalgoritmen som en kö, är den enda definierade gränsen för denna algoritm bandbredden på dess utdata.
Bandbreddsgränsen för anslutningen kan anges i ett trafikavtal . En bandbreddsgräns kan anges som ett paket- eller bildrutehastighet, en byte eller bithastighet eller som ett emissionsintervall mellan paketen.
Ineffektivitet
Implementeringen av den läckande hinken som en kö använder inte tillgängliga nätverksresurser effektivt. Eftersom den endast sänder paket med fasta intervall, kommer det att finnas många tillfällen då trafikvolymen är mycket låg och stora delar av nätverksresurserna (särskilt bandbredd) inte används. Därför finns det ingen mekanism i implementeringen av läckande hink som en kö för att tillåta individuella flöden att spricka upp till porthastighet, vilket effektivt förbrukar nätverksresurser vid tillfällen då det inte skulle finnas resurskonflikt i nätverket. Implementeringar av token-skopan och den läckande skopan som en mätare gör det dock möjligt för utgående trafikflöden att ha bristande egenskaper.
Jämförelse mellan de två versionerna
Analys av de två versionerna av leaky bucket-algoritmen visar att versionen som en kö är ett specialfall av versionen som en mätare.
Föreställ dig en trafikformningsfunktion för paket med fast längd som implementeras med hjälp av en kö med fast längd, som bildar ett fördröjningselement, som servas med en läckande hink som mätare. Föreställ dig också att hinken i denna mätare har ett djup som är lika med den mängd som tillförs av ett paket, dvs har ett gränsvärde, τ , på noll. Överensstämmelsetestet utförs dock endast vid intervall av emissionsintervallet, när paketet i spetsen av kön sänds och dess vatten tillsätts. Detta vatten läcker sedan bort under nästa emissionsintervall (eller tas bort precis innan nästa överensstämmelsetest utförs), vilket tillåter nästa paket att anpassa sig då eller vid något efterföljande emissionsintervall. Servicefunktionen kan också ses i termer av en token-hink med samma djup, där tillräckligt många tokens för ett paket läggs till (om hinken inte är full) vid utsläppsintervallen. Denna implementering kommer sedan att ta emot paket med ett bursty ankomstmönster (begränsat av ködjupet) och sända dem vidare med intervall som alltid är exakta (integral) multiplar av emissionsintervallet.
Implementeringen av den läckande skopan som en mätare (eller token-skopa) i en trafikformningsfunktion som beskrivs ovan är en exakt motsvarighet till beskrivningen av den läckande skopan som en kö: fördröjningselementet i mätarversionen är skopan för köversion; bucket av mätarversionen är den process som servar kön, och läckan är sådan att emissionsintervallet är detsamma som tick-intervallet. För paket med fast längd är implementeringen av den läckande hinken som en kö därför av ett specialfall av en trafikformningsfunktion som använder en läckande hink (eller token-hink) som en mätare där gränsvärdet, τ , är noll och processen av testningens överensstämmelse utförs med lägsta möjliga hastighet.
Den läckande hinken som kö för varierande paketlängder kan också beskrivas som likvärdig med ett specialfall av den läckande hinken som en meter. Den föreslagna implementeringen kan, liksom implementeringen med fast längd, ses som en trafikformningsfunktion där kön är ett fördröjningselement snarare än hinken, och funktionen som servar kön ges i detta fall uttryckligen som en token-bucket : den minskas för överensstämmande paket och inkrementeras med en fast hastighet. Därför, eftersom den läckande hinken som mätare och token-hinken är likvärdiga, är den läckande hinken som en kö för varierande paketlängder också ett specialfall av en trafikformningsfunktion som använder en läckande hink (eller token-hink) som en mätare.
Det finns en intressant konsekvens av att se den läckande hinken som en kö för varierande paketlängder som en specifik implementering av token-hinken eller den läckande hinken som en mätare i trafikformning. Detta är att mätarens hink har ett djup, n, och, som alltid är fallet med token-skopan, bestämmer detta djup burstiness av utgående trafik (kanske i förhållande till det genomsnittliga eller minsta antalet tokens som krävs av paket). Följaktligen är det möjligt att kvantifiera burstiness av utsignalen från denna "byte counting" läckande hink som en meter, såvida inte alla paket har den maximala längden när det blir meningslöst. Denna förmåga att definiera en burstiness för utgången är dock i direkt motsägelse till påståendet att den läckande hinken (som en kö) nödvändigtvis ger en utgång med en stel hastighet, oavsett hur bursty ingången.