Kvantpendel

Kvantpendeln är grundläggande för att förstå hindrade interna rotationer i kemi, kvantegenskaper hos spridningsatomer , såväl som många andra kvantfenomen. Även om en pendel som inte är föremål för liten vinkelapproximation har en inneboende olinjäritet, Schrödinger-ekvationen för det kvantiserade systemet lösas relativt enkelt.

Schrödinger ekvation

Med hjälp av lagrangemekanik från klassisk mekanik kan man utveckla en Hamiltonian för systemet. En enkel pendel har en generaliserad koordinat (vinkelförskjutningen $\phi$ ) och två begränsningar (strängens längd och rörelseplanet). De kinetiska och potentiella energierna i systemet kan konstateras vara

$T={\frac {1}{2}}ml^{2}{\dot {\phi }}^{2},$

$U=mgl(1-\cos \phi ).$

Detta resulterar i Hamiltonian

${\hat {H}}={\frac {{\hat {p}}^{2}}{2ml^{2}}}+mgl(1-\cos \phi ).$

Den tidsberoende Schrödinger-ekvationen för systemet är

$i\hbar {\frac {d\Psi }{dt}}=-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {d^{2}\Psi }{d\phi ^{2}}}+mgl(1-\cos \phi )\Psi .$

Man måste lösa den tidsoberoende Schrödinger-ekvationen för att hitta energinivåerna och motsvarande egentillstånd. Detta uppnås bäst genom att ändra den oberoende variabeln enligt följande:

$\eta =\phi +\pi ,$

$\Psi =\psi e^{-iEt/\hbar },$

$E\psi =-{\frac {\hbar ^{2}}{2ml^{2}}}{\frac {d^{2}\psi }{d\eta ^{2}}}+ mgl(1+\cos \eta )\psi .$

Detta är helt enkelt Mathieus differentialekvation

${\frac {d^{ 2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^ {3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,$

vars lösningar är Mathieu-funktioner .

Lösningar

Energier

Givet $q$ , för otaligt många specialvärden av $a$ , kallade karakteristiska värden , tillåter Mathieu-ekvationen lösningar som är periodiska med period $2\pi$ . De karakteristiska värdena för Mathieus cosinus, sinusfunktioner respektive skrivs ${\displaystyle a_{n}(q),b_{n}(q)} ,$ där $n$ är ett naturligt tal . De periodiska specialfallen för Mathieu cosinus- och sinusfunktionerna skrivs ofta $CE(n,q,x),SE(n,q ,x)$ respektive, även om de traditionellt ges en annan normalisering (nämligen att deras $L^{2}$ norm är lika med $\pi$ ).

Gränsvillkoren i kvantpendeln innebär att $a_{n}(q),b_{n}(q)$ är följande för en given $q$ :

${\frac {d^{ 2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^ {3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0,$

$a_{n}(q),b_{n}(q)={\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^ {3}}{\hbar ^{2}}}.$

Systemets energier, $E=mgl+{\frac {\hbar ^{2}a_{n}( q),b_{n}(q)}{2ml^{2}}}$ för jämna/udda lösningar, kvantiseras baserat på de karakteristiska värden som hittas genom att lösa Mathieu-ekvationen.

Det effektiva potentiella djupet kan definieras som

$q={\frac {m^{2}gl^{3}}{\hbar ^{2}}}.$

En djup potential ger en partikels dynamik i en oberoende potential. I kontrast, i en ytlig potential, Bloch-vågor , såväl som kvanttunnelering , av betydelse.

Allmän lösning

Den allmänna lösningen av differentialekvationen ovan för ett givet värde på a och q är en uppsättning linjärt oberoende Mathieu cosinus och Mathieu sines, som är jämna respektive udda lösningar. I allmänhet är Mathieu-funktionerna aperiodiska; för karakteristiska värden för $a_{n}(q),b_{n}(q)$ blir Mathieu cosinus och sinus periodiska med en period på $2\pi$ .

Egentillstånd

För positiva värden på q gäller följande:

$C(a_{n}(q),q,x)={ \frac {CE(n,q,x)}{CE(n,q,0)}},$

$S(b_{n}(q),q,x)={\frac {SE(n,q,x)}{SE'(n,q,0)}}.$

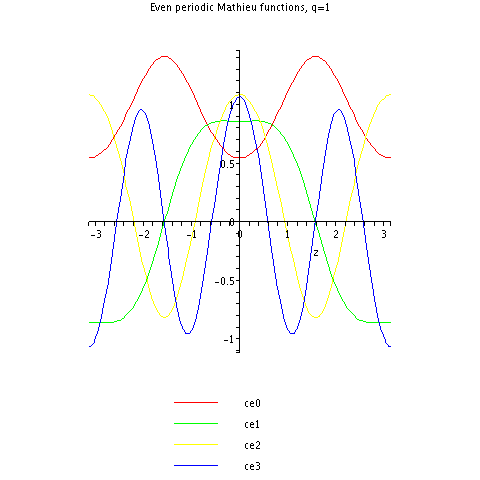
Här är de första periodiska Mathieu cosinusfunktionerna för $q=1$ .

Observera att till exempel $CE(1,1,x)$ (grön) liknar en cosinusfunktion, men med plattare kullar och grundare dalar.

Se även

• Kvantharmonisk oscillator

Bibliografi

•   Bransden, BH; Joachain, CJ (2000). Kvantmekanik (2:a upplagan). Essex: Pearson Education. ISBN 0-582-35691-1 .
•   Davies, John H. (2006). The Physics of Low-Dimensional Semiconductors: An Introduction (6:e upplagan). Cambridge University Press. ISBN 0-521-48491-X .
•   Griffiths, David J. (2004). Introduktion till kvantmekanik (2:a upplagan). Prentice Hall. ISBN 0-13-111892-7 .
• Muhammad Ayub, Atom Optics Quantum Pendulum , 2011, Islamabad, Pakistan., https://arxiv.org/abs/1012.6011