Kubanslutna cykler

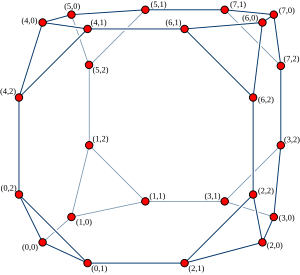
I grafteorin är de kubanslutna cyklerna en oriktad kubisk graf , bildad genom att ersätta varje hörn av en hyperkubgraf med en cykel . Det introducerades av Preparata & Vuillemin (1981) för användning som nätverkstopologi vid parallell beräkning .

Definition

De kubanslutna cyklerna av ordningen n (betecknas CCC _n ) kan definieras som en graf bildad från en uppsättning av n 2 ⁿ noder, indexerade med par av tal ( x , y ) där 0 ≤ x < 2 ⁿ och 0 ≤ y < n . Varje sådan nod är ansluten till tre grannar: ( x , ( y + 1) mod n ) , ( x , ( y − 1) mod n ) ) , och ( x ⊕ 2 ^y , y ) , där "⊕" betecknar den bitvisa exklusiva eller operationen på binära tal.

Denna graf kan också tolkas som resultatet av att ersätta varje vertex i en n -dimensionell hyperkubgraf med en n -vertexcykel. Hyperkubgrafens hörn indexeras med siffrorna x och positionerna inom varje cykel med siffrorna y .

Egenskaper

De kubanslutna cyklerna av ordning n är Cayley-grafen för en grupp som verkar på binära ord med längden n genom att rotera och vända bitar av ordet. Generatorerna som används för att bilda denna Cayley-graf från gruppen är de gruppelement som fungerar genom att rotera ordet en position åt vänster, rotera det en position åt höger eller vända dess första bit. Eftersom det är en Cayley-graf är den vertextransitiv : det finns en symmetri hos grafen som kartlägger vilken vertex som helst till vilken annan vertex som helst.

Diametern på de kubanslutna cyklerna av ordning n är 2 n + ⌊n/2⌋ − 2 för alla n ≥ 4; punkten längst bort från ( x , y ) är (2 ⁿ − x − 1, ( y + n /2) mod n ). Sýkora & Vrťo (1993) visade att korsningstalet för CCC _n är ((1/20) + o(1)) 4 ⁿ .

Enligt Lovász-förmodan ska den kubanslutna cykelgrafen alltid innehålla en Hamiltonsk cykel , och detta är nu känt för att vara sant. Mer generellt, även om dessa grafer inte är pancykliska , innehåller de cykler av alla utom ett begränsat antal möjliga jämna längder, och när n är udda innehåller de också många av de möjliga udda längderna av cykler.

Parallell bearbetning ansökan

Kubanslutna cykler undersöktes av Preparata & Vuillemin (1981), som tillämpade dessa grafer som sammankopplingsmönstret för ett nätverk som förbinder processorerna i en parallell dator . I den här applikationen har kubanslutna cykler anslutningsfördelarna med hyperkuber samtidigt som de bara kräver tre anslutningar per processor. Preparata och Vuillemin visade att en plan layout baserad på detta nätverk har optimal area × tid ² komplexitet för många parallella bearbetningsuppgifter.

Anteckningar

Akers, Sheldon B.; Krishnamurthy, Balakrishnan (1989), "A group-theoretic model for symmetric interconnection networks", IEEE Transactions on Computers , 38 (4): 555–566, doi : 10.1109/12.21148 .
Annexstein, Fred; Baumslag, Marc; Rosenberg, Arnold L. (1990), "Group action graphs and parallel architectures", SIAM Journal on Computing , 19 (3): 544–569, doi : 10.1137/0219037 .
Friš, Ivan; Havel, Ivan; Liebl, Petr (1997), "The diameter of the cube-connected cycles", Information Processing Letters , 61 (3): 157–160, doi : 10.1016/S0020-0190(97)00013-6 .
Germa, Anne; Heydemann, Marie-Claude; Sotteau, Dominique (1998), "Cycles in the cube-connected cycles graph", Discrete Applied Mathematics , 83 (1–3): 135–155, doi : 10.1016/S0166-218X(98)80001-2 , MR 68 6 .
Preparata, Franco P .; Vuillemin, Jean (1981), "The cube-connected cycles: a mångsidigt nätverk för parallell beräkning", Communications of the ACM , 24 (5): 300–309, doi : 10.1145/358645.358660 , hdl : 42172/5 , S : 42172/7 .
Sykora, Ondrej; Vrťo, Imrich (1993), "On crossing numbers of hypercubes and cube connected cycles", BIT Numerical Mathematics , 33 (2): 232–237, doi : 10.1007/BF01989746 , hdl : 110001-02001-02001/02-02 92E4-9 , S2CID 15913153 .