Kovarians och kontravarians (datavetenskap)
| Typsystem |
|---|
| Allmänna begrepp |
| Huvudkategorier |
|
| Mindre kategorier |
Många typsystem för programmeringsspråk stöder subtyping . Till exempel, om typen Cat är en undertyp av Animal , bör ett uttryck av typen Cat vara utbytbart varhelst ett uttryck av typen Animal används.
Varians hänvisar till hur subtypning mellan mer komplexa typer relaterar till subtyping mellan deras komponenter. Till exempel, hur ska en lista över katter relatera till en lista över djur ? Eller hur ska en funktion som returnerar Cat relatera till en funktion som returnerar Animal ?
typkonstruktorns varians kan subtypningsrelationen för de enkla typerna antingen bevaras, omvändas eller ignoreras för respektive komplexa typer. I OCaml , till exempel, är "list of Cat" en undertyp av "list of Animal" eftersom listtypens konstruktor är kovariant . Detta innebär att subtypningsrelationen för de enkla typerna bevaras för de komplexa typerna.
Å andra sidan är "funktion från djur till sträng" en undertyp av "funktion från katt till sträng" eftersom funktionstypens konstruktor är kontravariant i parametertypen. Här är subtypningsrelationen för de enkla typerna omvänd för de komplexa typerna.
Med andra ord är kovarians kvaliteten på att vara annorlunda genom att vara mer specifik ( Katt är samvariant till djur ) medan kontravarians är kvaliteten på att vara annorlunda genom att vara mer allmän ( Djur är kontravariant mot katt ).
En programmeringsspråksdesigner kommer att överväga varians när han utformar skrivregler för språkfunktioner som arrayer, arv och generiska datatyper . Genom att göra typkonstruktörer samvarianta eller kontravarianta istället för invarianta, kommer fler program att accepteras som välskrivna. Å andra sidan tycker programmerare ofta att kontravarians är ointuitiv, och exakt spårning av varians för att undvika runtime-typfel kan leda till komplexa skrivregler.
För att hålla typsystemet enkelt och tillåta användbara program kan ett språk behandla en typkonstruktor som invariant även om det skulle vara säkert att betrakta det som en variant, eller behandla det som samvariant även om det skulle kunna bryta mot typsäkerheten.
Formell definition
Inom typsystemet för ett programmeringsspråk är en skrivregel eller en typkonstruktor:
-
samvariant om den bevarar ordningen av typer (≤) , vilket sorterar typer från mer specifika till mer generiska: Om
A ≤ B, dåI<A> ≤ I<B>; -
kontravariant om den vänder denna ordning: Om
A ≤ B, dåI<B> ≤ I<A>; -
bivariant om båda dessa gäller (dvs. om
A ≤ B, dåI<A> ≡ I<B>); - variant om kovariant, kontravariant eller bivariant;
- invariant eller nonvariant om inte variant.
Artikeln överväger hur detta gäller för några vanliga typkonstruktörer.
C# exempel
Till exempel, i C# , om Cat är en undertyp av Animal , då:
-
IEnumerable < Cat >är en undertyp avIEnumerable < Animal >. Subtypningen bevaras eftersomIEnumerable < T >är samvariant påT. -
Action < Animal >är en undertyp avAction < Cat >. Subtypningen är omvänd eftersomAction < T >är kontravariant påT. - Varken
IList < Katt >ellerIList < Djur >är en subtyp av den andra, eftersomIList < T >är invariant påT.
Variansen för ett generiskt C#-gränssnitt deklareras genom att placera ut (covariant) eller in (kontravariant) attributet på (noll eller fler av) dess typparametrar. För varje så märkt typparameter verifierar kompilatorn slutgiltigt, med varje överträdelse som är dödlig, att sådan användning är globalt konsekvent. Ovanstående gränssnitt deklareras som IEnumerable < ut T > , Action < in T > och IList < T > . Typer med mer än en typparameter kan ange olika varianser för varje typparameter. Till exempel representerar delegattypen Func < in T , out TResult > en funktion med en kontravariant indataparameter av typ T och ett kovariant returvärde av typen TResult .
Skrivningsreglerna för gränssnittsvarians säkerställer typsäkerhet. Till exempel representerar en Action < T > en förstklassig funktion som förväntar sig ett argument av typen T , och en funktion som kan hantera vilken typ av djur som helst kan alltid användas istället för en som bara kan hantera katter.
Matriser
Skrivskyddade datatyper (källor) kan vara samvarierande; skrivbara datatyper (sänkor) kan vara motsatta. Föränderliga datatyper som fungerar som både källor och sänkor bör vara oföränderliga. För att illustrera detta allmänna fenomen, överväg arraytypen . För typen Djur kan vi göra typen Djur [] , som är en "uppsättning av djur". För detta exempel stöder denna array både läs- och skrivelement.
Vi har möjlighet att behandla detta som antingen:
- kovariant: en
katt []är ettdjur []; - kontravariant: ett
djur []är enkatt []; - invariant: ett
djur []är inte enkatt []och enkatt []är inte ettdjur [].
Om vi vill undvika typfel är endast det tredje valet säkert. Uppenbarligen kan inte alla djur [] behandlas som om det vore en katt [] , eftersom en klient som läser från arrayen förväntar sig en katt , men ett djur [] kan innehålla t.ex. en hund . Så den kontravarierande regeln är inte säker.
Omvänt kan en katt [] inte behandlas som ett djur [] . Det ska alltid vara möjligt att sätta in en hund i ett djur [] . Med kovarianta arrayer kan det inte garanteras att det är säkert, eftersom stödbutiken faktiskt kan vara en rad katter. Så den kovariansregeln är inte heller säker – arraykonstruktorn bör vara invariant . Observera att detta endast är ett problem för föränderliga arrayer; den kovarianta regeln är säker för oföränderliga (skrivskyddade) arrayer. På samma sätt skulle den kontravarierande regeln vara säker för skrivbara arrayer.
Med C# kan du leka runt detta genom att använda det dynamiska nyckelordet över array/collection/generics med duck typing , intellisense går förlorad på detta sätt men det fungerar.
Kovarianta arrayer i Java och C#
Tidiga versioner av Java och C# inkluderade inte generika, även kallad parametrisk polymorfism . I en sådan miljö utesluter att göra arrayer invarianta användbara polymorfa program.
Överväg till exempel att skriva en funktion för att blanda en array, eller en funktion som testar två arrayer för likhet med hjälp av Object . är lika med metod på elementen. Implementeringen beror inte på den exakta typen av element som lagras i arrayen, så det borde vara möjligt att skriva en enda funktion som fungerar på alla typer av arrayer. Det är lätt att implementera funktioner av typen:
boolean equalArrays ( Objekt [] a1 , Objekt [] a2 ); void shuffleArray ( Objekt [] a );
Men om arraytyper skulle behandlas som invarianta skulle det bara vara möjligt att anropa dessa funktioner på en array av exakt typen Objekt [] . Man kunde till exempel inte blanda en rad strängar.
Därför behandlar både Java och C# arraytyper kovariant. Till exempel, i Java sträng [] en undertyp av objekt [] , och i C# är sträng [] en undertyp av objekt [] .
Som diskuterats ovan leder kovarianta arrayer till problem med att skriva in i arrayen. Java och C# hanterar detta genom att markera varje arrayobjekt med en typ när det skapas. Varje gång ett värde lagras i en array kommer exekveringsmiljön att kontrollera att runtime-typen för värdet är lika med runtime-typen för arrayen. Om det finns en missmatchning, kastas en ArrayStoreException (Java) eller ArrayTypeMismatchException (C#):
0 // a är en array med ett element av String String [] a = new String [ 1 ] ; // b är en array av objektobjekt [ ] b = a ; // Tilldela ett heltal till b. Detta skulle vara möjligt om b verkligen var // en array av Object, men eftersom det verkligen är en array av String, // kommer vi att få en java.lang.ArrayStoreException. b [ ] = 1 ;
I exemplet ovan kan man läsa från arrayen (b) säkert. Det är bara att försöka skriva till arrayen som kan leda till problem.
En nackdel med detta tillvägagångssätt är att det lämnar möjligheten till ett körtidsfel som ett strängare system kunde ha fångat vid kompilering. Dessutom skadar det prestandan eftersom varje skrivning i en array kräver en extra körtidskontroll.
Med tillägg av generika erbjuder Java och C# nu sätt att skriva den här typen av polymorfa funktioner utan att förlita sig på kovarians. Funktionerna för arrayjämförelse och blandning kan ges de parametriserade typerna
< T > booleska likaArrays ( T [] a1 , T [] a2 ); < T > void shuffleArray ( T [] a );
Alternativt, för att framtvinga att en C#-metod kommer åt en samling på ett skrivskyddat sätt, kan man använda gränssnittet IEnumerable < object > istället för att skicka det ett array- objekt [] .
Funktionstyper
Språk med förstklassiga funktioner har funktionstyper som "en funktion som förväntar sig en katt och returnerar ett djur" (skrivs Cat -> Animal i OCaml- syntax eller Func < Cat , Animal > i C# -syntax).
Dessa språk måste också specificera när en funktionstyp är en undertyp till en annan - det vill säga när det är säkert att använda en funktion av en typ i ett sammanhang som förväntar sig en funktion av en annan typ. Det är säkert att ersätta en funktion f för en funktion g om f accepterar en mer allmän typ av argument och returnerar en mer specifik typ än g . Till exempel kan funktioner av typen Djur -> Katt , Katt -> Katt och Djur -> Djur användas varhelst en Katt -> Djur förväntades. (Man kan jämföra detta med robusthetsprincipen för kommunikation: "var liberal i det du accepterar och konservativ i det du producerar.") Den allmänna regeln är:
- om och .
Genom att använda inferensregelnotation kan samma regel skrivas som:
Med andra ord, → typkonstruktorn är kontravariant i parametern (input) typ och kovarian i retur (output) typen . Denna regel angavs först formellt av John C. Reynolds och populariserades ytterligare i ett papper av Luca Cardelli .
När man hanterar funktioner som tar funktioner som argument kan denna regel tillämpas flera gånger. Till exempel, genom att tillämpa regeln två gånger ser vi att om . Med andra ord, typen är samvariant i positionen för . För komplicerade typer kan det vara förvirrande att mentalt spåra varför en given typspecialisering är eller inte är typsäker, men det är lätt att beräkna vilka positioner som är ko- och kontravarianta: en position är samvariant om den är på vänster sida av ett jämnt antal pilar som gäller för den.
Arv i objektorienterade språk
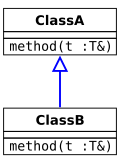
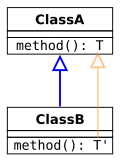
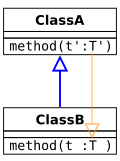
När en underklass åsidosätter en metod i en superklass måste kompilatorn kontrollera att den överordnade metoden har rätt typ. Även om vissa språk kräver att typen exakt matchar typen i superklassen (invarians), är det också typsäkert att tillåta den överordnade metoden att ha en "bättre" typ. Med den vanliga subtypningsregeln för funktionstyper innebär detta att den överordnade metoden ska returnera en mer specifik typ (covarians av returtyp) och acceptera ett mer generellt argument (parametertypkontravarians). I UML- notation är möjligheterna följande (där Klass B är underklassen som utökar Klass A som är superklassen):
- Varians och överordnad metod: översikt
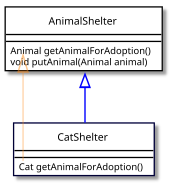
För ett konkret exempel, anta att vi skriver en klass för att modellera ett djurhem . Vi antar att Cat är en underklass till Animal , och att vi har en basklass (med Java-syntax)
class AnimalShelter { Animal getAnimalForAdoption () { // ... } void putAnimal ( Animal animal ) { //... } }
Nu är frågan: om vi underklassar AnimalShelter , vilka typer får vi ge för att fåAnimalForAdoption och putAnimal ?
Kovariant metod returtyp
I ett språk som tillåter kovarianta returtyper kan en härledd klass åsidosätta getAnimalForAdoption- metoden för att returnera en mer specifik typ:
class CatShelter utökar AnimalShelter { Cat getAnimalForAdoption () { return new Cat (); } }
Bland de vanliga OO-språken stöder Java , C++ och C# (från och med version 9.0 ) kovarianta returtyper. Att lägga till den kovarianta returtypen var en av de första ändringarna av C++-språket som godkändes av standardkommittén 1998. Scala och D stöder också kovariansreturtyper.
Paravariant metod parametertyp
På samma sätt är det typsäkert att tillåta en överordnad metod att acceptera ett mer generellt argument än metoden i basklassen:
klass CatShelter utökar AnimalShelter { void putAnimal ( Object animal ) { // ... } }
Endast ett fåtal objektorienterade språk tillåter faktiskt detta (till exempel Python när typkontrollerad med mypy). C++, Java och de flesta andra språk som stöder överbelastning och/eller skuggning skulle tolka detta som en metod med ett överbelastat eller skuggat namn.
Sather stödde dock både kovarians och kontravarians. Anropskonventioner för åsidosatta metoder är kovarianta utan parametrar och returvärden, och kontravarianta med normala parametrar (med läget i ).
Kovariant metod parametertyp
Ett par vanliga språk, Eiffel och Dart , tillåter att parametrarna för en överordnad metod har en mer specifik typ än metoden i superklassen (parametertypskovarians). Följande Dart-kod skulle alltså skriva check, med putAnimal som åsidosätter metoden i basklassen:
klass CatShelter utökar AnimalShelter { void putAnimal ( samvariant kattdjur ) { // ... } }
Detta är inte typsäkert. Genom att bygga upp ett CatShelter till ett AnimalShelter kan man försöka placera en hund i ett katthem. Det uppfyller inte CatShelter- parameterbegränsningarna och kommer att resultera i ett körtidsfel. Bristen på typsäkerhet (känd som "catcall-problemet" i Eiffelgemenskapen, där "katt" eller "CAT" är en ändrad tillgänglighet eller typ) har varit ett långvarigt problem. Under årens lopp har olika kombinationer av global statisk analys, lokal statisk analys och nya språkfunktioner föreslagits för att råda bot på det, och dessa har implementerats i vissa Eiffel-kompilatorer.
Trots typsäkerhetsproblemet anser Eiffeldesignerna kovarianta parametertyper som avgörande för att modellera verkliga krav. Katthemmet illustrerar ett vanligt fenomen: det är ett slags djurhem men har ytterligare begränsningar , och det verkar rimligt att använda arv och begränsade parametertyper för att modellera detta. Genom att föreslå denna användning av arv, förkastar Eiffeldesignerna Liskov-substitutionsprincipen , som säger att objekt av underklasser alltid bör vara mindre begränsade än objekt i deras superklass.
Ett annat exempel på ett vanligt språk som tillåter kovarians i metodparametrar är PHP när det gäller klasskonstruktörer. I följande exempel accepteras metoden __construct() trots att metodparametern är samvariant med förälderns metodparameter. Om den här metoden var något annat än __construct(), skulle ett fel inträffa:
gränssnitt AnimalInterface {} gränssnitt DogInterface utökar AnimalInterface {} class Dog implementerar DogInterface {} class Pet { public function __construct ( AnimalInterface $animal ) {} } class PetDog utökar Pet { public function __construct ( DogInterface $dog ) { parent :: __construct ( $ hund ); } }
Ett annat exempel där samvarianta parametrar verkar vara till hjälp är så kallade binära metoder, det vill säga metoder där parametern förväntas vara av samma typ som objektet metoden anropas på. Ett exempel är compareTo -metoden: a . compareTo ( b ) kontrollerar om a kommer före eller efter b i någon ordning, men sättet att jämföra, säg, två rationella tal kommer att skilja sig från sättet att jämföra två strängar. Andra vanliga exempel på binära metoder inkluderar likhetstester, aritmetiska operationer och uppsättningsoperationer som delmängd och union.
I äldre versioner av Java specificerades jämförelsemetoden som ett gränssnitt Comparable :
gränssnitt Comparable { int compareTo ( Objekt o ); }
Nackdelen med detta är att metoden är specificerad att ta ett argument av typen Object . En typisk implementering skulle först kasta ner detta argument (att kasta ett fel om det inte är av den förväntade typen):
class RationalNumber implementerar Comparable { int numerator ; int nämnare ; // ... public int compareTo ( Object other ) { RationalNumber otherNum = ( RationalNumber ) other ; returnera heltal . jämföra ( täljare * annanNum . nämnare , annanNum . täljare * nämnare ); } }
I ett språk med kovarianta parametrar kan argumentet för compareTo direkt ges den önskade typen RationalNumber , vilket döljer typcasten. (Detta skulle naturligtvis fortfarande ge ett körtidsfel om compareTo sedan anropades på t.ex. en sträng .)
Undviker behovet av samvarierande parametertyper
Andra språkfunktioner kan ge de uppenbara fördelarna med samvarianta parametrar samtidigt som Liskovs utbytbarhet bevaras.
I ett språk med generika (alias parametrisk polymorfism ) och gränsad kvantifiering kan de tidigare exemplen skrivas på ett typsäkert sätt. Istället för att definiera AnimalShelter definierar vi en parametriserad klass Shelter <T> . (En nackdel med detta är att implementeraren av basklassen måste förutse vilka typer som måste vara specialiserade på underklasserna.)
class Shelter < T extends Animal > { T getAnimalForAdoption () { // ... } void putAnimal ( T animal ) { // ... } } class CatShelter utökar Shelter < Cat > { Cat getAnimalForAdoption () { // .. . } void putAnimal ( Kattdjur ) { // ... } }
det jämförbara gränssnittet i de senaste versionerna av Java parametrats, vilket gör att nedsändningen kan utelämnas på ett typsäkert sätt:
class RationalNumber implementerar Comparable < RationalNumber > { int numerator ; int nämnare ; // ... public int compareTo ( RationalNumber otherNum ) { return Heltal . jämföra ( täljare * annanNum . nämnare , annanNum . täljare * nämnare ); } }
En annan språkfunktion som kan hjälpa är multipel utskick . En anledning till att binära metoder är besvärliga att skriva är att i ett anrop som en . compareTo ( b ) , val av korrekt implementering av compareTo beror verkligen på körtidstypen för både a och b , men i ett konventionellt OO-språk tas bara hänsyn till körtidstypen för a . I ett språk med Common Lisp Object System (CLOS)-liknande multipelutskick , kan jämförelsemetoden skrivas som en generisk funktion där båda argumenten används för metodval.
Giuseppe Castagna observerade att i ett maskinskrivet språk med flera sändningar kan en generisk funktion ha vissa parametrar som styr sändningen och vissa "överblivna" parametrar som inte har det. Eftersom metodvalsregeln väljer den mest specifika tillämpliga metoden, om en metod åsidosätter en annan metod, kommer den åsidosättande metoden att ha mer specifika typer för de styrande parametrarna. Å andra sidan, för att säkerställa typsäkerhet måste språket fortfarande kräva att de överblivna parametrarna är minst lika allmänna. Med den tidigare terminologin är typer som används för val av körningsmetod samvariant medan typer som inte används för val av körningsmetod av metoden är kontravarianta. Konventionella ensändningsspråk som Java följer också denna regel: endast ett argument används för metodval (mottagarobjektet skickas vidare till en metod som det dolda argumentet detta ), och faktiskt är typen av detta mer specialiserad inom överordnade metoder än i superklassen.
Castagna föreslår att exempel där kovarianta parametertyper är överlägsna (särskilt binära metoder) bör hanteras med hjälp av multipel sändning; som är naturligt samvariant. De flesta programmeringsspråk stöder dock inte multipel sändning.
Sammanfattning av varians och arv
Följande tabell sammanfattar reglerna för åsidosättande av metoder på de språk som diskuterats ovan.
| Parametertyp | Returtyp | |
|---|---|---|
| C++ (sedan 1998), Java (sedan J2SE 5.0 ), D | Invariant | Kovariant |
| C# | Invariant | Kovariant (sedan C# 9 - före Invariant) |
| Scala , Sather | Kontravariant | Kovariant |
| Eiffel | Kovariant | Kovariant |
Generiska typer
I programmeringsspråk som stöder generika (alias parametrisk polymorfism ) kan programmeraren utöka typsystemet med nya konstruktörer. Till exempel gör ett C#-gränssnitt som IList < T > det möjligt att konstruera nya typer som IList < Animal > eller IList < Cat > . Frågan uppstår då vad variansen för dessa typkonstruktörer bör vara.
Det finns två huvudsakliga tillvägagångssätt. På språk med variansanteckningar för deklarationsplats (t.ex. C# ), kommenterar programmeraren definitionen av en generisk typ med den avsedda variansen för dess typparametrar. Med variansanteckningar för användningsplats (t.ex. Java ), annoterar programmeraren istället platserna där en generisk typ instansieras.
Anteckningar om avvikelse på deklarationsplats
De mest populära språken med variansanteckningar för deklarationsplats är C# och Kotlin (med nyckelorden ut och in ), och Scala och OCaml (med nyckelorden + och - ). C# tillåter endast varianskommentarer för gränssnittstyper, medan Kotlin, Scala och OCaml tillåter dem för både gränssnittstyper och konkreta datatyper.
Gränssnitt
I C# kan varje typparameter i ett generiskt gränssnitt markeras som kovariant ( ut ), kontravariant ( in ) eller invariant (ingen anteckning). Till exempel kan vi definiera ett gränssnitt IEnumerator < T > av skrivskyddade iteratorer, och deklarera att det är kovariant (out) i sin typparameter.
gränssnitt IEnumerator < ut T > { T Aktuell { get ; } bool MoveNext (); }
Med denna deklaration kommer IEnumerator att behandlas som kovariant i sin typparameter, t.ex. IEnumerator < Cat > är en undertyp av IEnumerator < Animal > .
Typkontrollen tvingar fram att varje metoddeklaration i ett gränssnitt endast nämner typparametrarna på ett sätt som överensstämmer med in / ut -annoteringarna. Det vill säga, en parameter som förklarades samvariant får inte förekomma i några kontravarianta positioner (där en position är kontravariant om den förekommer under ett udda antal kontravarianta typkonstruktorer). Den exakta regeln är att returtyperna för alla metoder i gränssnittet måste vara giltiga kovariant och alla metodparametertyper måste vara giltiga kontravariant , där giltig S-ly definieras enligt följande:
- Icke-generiska typer (klasser, strukturer, enums, etc.) är giltiga både ko- och kontravariant.
- En typparameter
Tär giltig kovariant om den inte markeratsin, och giltig kontravariant om den intemarkerats. - En array typ
A []är giltig S-ly omAär. (Detta beror på att C# har kovarianta arrayer.) - En generisk typ
G < A1 , A2 , ..., An >är giltig S-ly om för varje parameterAi,- Ai är giltig S-ly, och den i: te parametern till
Gdeklareras kovariant, eller - Ai är giltig (inte S)-ly, och den i: te parametern till
Gförklaras kontravariant, eller - Ai är giltig både kovariant och kontravariant, och den i: te parametern till
Gförklaras invariant.
- Ai är giltig S-ly, och den i: te parametern till
Som ett exempel på hur dessa regler gäller, betrakta gränssnittet IList < T > .
gränssnitt IList < T > { void Insert ( int index , T item ); IEnumerator < T > GetEnumerator (); }
Parametertypen T för Insert måste vara giltig kontravariant, dvs. typparametern T får inte taggas ut . På samma sätt måste resultattypen IEnumerator < T > för GetEnumerator vara giltig kovariant, dvs (eftersom IEnumerator är ett kovariansgränssnitt) måste typen T vara giltig kovariant, dvs typparametern T får inte vara taggad i . Detta visar att gränssnittet IList inte får markeras vare sig co- eller contravariant.
I det vanliga fallet med en generisk datastruktur som IList innebär dessa begränsningar att en ut -parameter endast kan användas för metoder för att få ut data från strukturen, och en in -parameter kan endast användas för metoder som lägger in data i strukturen, därför valet av sökord.
Data
C# tillåter varianskommentarer på parametrarna för gränssnitt, men inte parametrarna för klasser. Eftersom fält i C#-klasser alltid är föränderliga, skulle variantparametriserade klasser i C# inte vara särskilt användbara. Men språk som betonar oföränderlig data kan göra bra användning av kovarianta datatyper. Till exempel, i hela Scala , Kotlin och OCaml är den oföränderliga listtypen samvariant: List [ Cat ] är en undertyp av List [ Animal ] .
Scalas regler för att kontrollera varianskommentarer är i huvudsak desamma som C#s. Det finns dock vissa idiom som gäller framför allt oföränderliga datastrukturer. De illustreras av följande (utdrag ur) definitionen av klassen List [ A ] .
förseglad abstrakt klass Lista [ + A ] förlänger AbstractSeq [ A ] { def head : A def tail : List [ A ] /** Lägger till ett element i början av denna lista. */ def :: [ B >: A ] ( x : B ): Lista [ B ] = ny skala . samling . oföränderlig . :: ( x , detta ) /** ... */ }
För det första måste klassmedlemmar som har en varianttyp vara oföränderliga. Här huvud typen A , som förklarades kovariant ( + ), och faktiskt huvud deklarerades som en metod ( def ). Att försöka förklara det som ett föränderligt fält ( var ) skulle avvisas som typfel.
För det andra, även om en datastruktur är oföränderlig, kommer den ofta att ha metoder där parametertypen förekommer kontravariant. Tänk till exempel på metoden :: som lägger till ett element längst fram i en lista. (Implementeringen fungerar genom att skapa ett nytt objekt av den liknande namngivna klassen :: , klassen av icke-tomma listor.) Den mest uppenbara typen att ge det skulle vara
def :: ( x : A ): Lista [ A ]
Detta skulle dock vara ett typfel, eftersom den kovarianta parametern A uppträder i en kontravariant position (som en funktionsparameter). Men det finns ett knep för att komma runt det här problemet. Vi ger :: en mer allmän typ, som gör det möjligt att lägga till ett element av vilken typ B som helst så länge som B är en supertyp av A . Observera att detta förlitar sig på List är samvariant, eftersom den har typen List [ A ] och vi behandlar den som att den har typen List [ B ] . Vid första anblicken är det kanske inte uppenbart att den generaliserade typen är sund, men om programmeraren börjar med den enklare typdeklarationen kommer typfelen att peka ut platsen som behöver generaliseras.
Att sluta sig till varians
Det är möjligt att designa ett typsystem där kompilatorn automatiskt härleder de bästa möjliga varianskommentarerna för alla datatypparametrar. Analysen kan dock bli komplex av flera anledningar. För det första är analysen icke-lokal eftersom variansen för ett gränssnitt I beror på variansen för alla gränssnitt som jag nämner. För det andra, för att få unika bästa lösningar måste typsystemet tillåta bivarianta parametrar (som samtidigt är ko- och kontravarianta). Och slutligen, variansen av typparametrar borde utan tvekan vara ett medvetet val av designern av ett gränssnitt, inte något som bara händer.
Av dessa skäl gör de flesta språk väldigt lite variansinferens. C# och Scala drar inga slutsatser om varianskommentarer alls. OCaml kan härleda variansen av parametriserade konkreta datatyper, men programmeraren måste explicit specificera variansen för abstrakta typer (gränssnitt).
Tänk till exempel på en OKaml-datatyp T som omsluter en funktion
typ ( ' a , ' b ) t = T av ( ' a -> ' b )
Kompilatorn kommer automatiskt att dra slutsatsen att T är kontravariant i den första parametern och samvariant i den andra. Programmeraren kan också tillhandahålla explicita kommentarer, som kompilatorn kontrollerar är nöjda. Följande deklaration motsvarar alltså den föregående:
typ (- ' a , + ' b ) t = T av ( ' a -> ' b )
Explicita anteckningar i OKaml blir användbara när du anger gränssnitt. Till exempel standardbiblioteksgränssnittet Map . S för associationstabeller inkluderar en anteckning som säger att karttypskonstruktorn är kovariant i resultattypen.
modultyp S = sig typ nyckeltyp ( + ' a ) t val tom : ' a t val mem : nyckel -> ' a t - > bool ... slut
Detta säkerställer att t.ex. cat IntMap . t är en undertyp av djur IntMap . t .
Använd webbplatsvariansannoteringar (jokertecken)
En nackdel med deklarationsplatsmetoden är att många gränssnittstyper måste göras oföränderliga. Till exempel såg vi ovan att IList behövde vara invariant, eftersom den innehöll både Insert och GetEnumerator . För att exponera mer varians kan API-designern tillhandahålla ytterligare gränssnitt som tillhandahåller delmängder av de tillgängliga metoderna (t.ex. en "endast infogningslista" som bara tillhandahåller Insert ). Detta blir dock snabbt otympligt.
Användningsplatsavvikelse betyder att den önskade avvikelsen indikeras med en anteckning på den specifika platsen i koden där typen kommer att användas. Detta ger användare av en klass fler möjligheter till subtyping utan att kräva att designern av klassen definierar flera gränssnitt med olika varians. Istället, vid den tidpunkt då en generisk typ instansieras till en faktisk parametriserad typ, kan programmeraren indikera att endast en delmängd av dess metoder kommer att användas. I själva verket gör varje definition av en generisk klass också tillgängliga gränssnitt för de kovarianta och kontravarianta delarna av den klassen.
Java tillhandahåller variansanteckningar för användningsplatser genom jokertecken , en begränsad form av avgränsade existentiella typer . En parameteriserad typ kan instansieras med ett jokertecken ? tillsammans med en övre eller nedre gräns, t.ex. Lista <? utökar Animal > eller _ List <? superdjur > . Ett obegränsat jokertecken som List <?> är likvärdigt med List <? utökar Objekt > . En sådan typ representerar List < X > för någon okänd typ X som uppfyller gränsen. Till exempel, om l har typen List <? utökar Animal > , då accepterar typkontrollen
Djur a = l . få ( 3 );
eftersom typ X är känd för att vara en undertyp av Animal , men
l . add ( nytt djur ());
kommer att avvisas som ett typfel eftersom ett djur inte nödvändigtvis är ett X . I allmänhet, givet något gränssnitt I < T > , en referens till ett I <? utökar T > förbjuder att använda metoder från gränssnittet där T förekommer kontravariant i typen av metod. Omvänt, om jag hade typen . List <? superdjur > man skulle kunna kalla l lägg till men inte l . få .
Medan parametriserade typer av icke-jokertecken i Java är invarianta (t.ex. finns det inget subtypningsförhållande mellan List < Katt > och List < Djur > ), kan jokerteckentyper göras mer specifika genom att ange en snävare gräns. Till exempel Lista <? utökar Cat > är en undertyp av List <? sträcker sig Djur > . Detta visar att jokerteckentyper är samvarierande i sina övre gränser (och även kontravarianta i sina nedre gränser) . Totalt, givet en jokerteckentyp som C <? förlänger T > finns det tre sätt att bilda en undertyp: genom att specialisera klassen C , genom att ange en snävare bunden T , eller genom att ersätta jokertecknet ? med en specifik typ (se figur).
Genom att tillämpa två av ovanstående tre former av subtypning blir det möjligt att till exempel skicka ett argument av typen List < Cat > till en metod som förväntar sig en List <? sträcker sig Djur > . Detta är den typ av uttrycksfullhet som är resultatet av kovarianta gränssnittstyper. Typen List <? extends Animal > fungerar som en gränssnittstyp som endast innehåller de kovarianta metoderna för List < T > , men implementeraren av List < T > behövde inte definiera det i förväg.
I det vanliga fallet med en generisk datastruktur IList används kovarianta parametrar för metoder för att få ut data från strukturen, och kontravarianta parametrar för metoder som lägger in data i strukturen. Mnemoniken för Producer Extends, Consumer Super (PECS), från boken Effective Java av Joshua Bloch ger ett enkelt sätt att komma ihåg när man ska använda kovarians och kontravarians.
Jokertecken är flexibla, men det finns en nackdel. Medan användningsplatsvarians innebär att API-designers inte behöver överväga varians av typparametrar till gränssnitt, måste de ofta istället använda mer komplicerade metodsignaturer. Ett vanligt exempel är gränssnittet Comparable . Anta att vi vill skriva en funktion som hittar det största elementet i en samling. Elementen måste implementera compareTo -metoden, så ett första försök kan vara
< T sträcker sig Jämförbar < T >> T max ( Samling < T > coll );
Den här typen är dock inte tillräckligt generell – man kan hitta maxvärdet för en samling < Kalender > samling < Gregoriansk kalender > , men inte en . Problemet är att GregorianCalendar inte implementerar Comparable < GregorianCalendar > , utan istället det (bättre) gränssnittet Comparable < Calendar > . I Java, till skillnad från i C#, Comparable < Calendar > inte vara en undertyp av Comparable < GregorianCalendar > . Istället måste typen av max ändras:
< T sträcker sig Jämförbar <? super T >> T max ( Collection < T > coll );
Det avgränsade jokertecken ? super T förmedlar informationen som max anropar endast kontravarierande metoder från det jämförbara gränssnittet. Det här exemplet är frustrerande eftersom alla metoder i Comparable är kontravarierande, så det villkoret är trivialt sant. Ett system för deklarationsplats skulle kunna hantera det här exemplet med mindre röran genom att endast kommentera definitionen av Comparable .
Jämför anteckningar om deklarationsplats och användningsplats
Anteckningar om användningsplatsavvikelse ger ytterligare flexibilitet, vilket gör att fler program kan skriva kontroll. De har dock fått kritik för den komplexitet de lägger till språket, vilket leder till komplicerade typsignaturer och felmeddelanden.
Ett sätt att bedöma om den extra flexibiliteten är användbar är att se om den används i befintliga program. En undersökning av en stor uppsättning Java-bibliotek visade att 39 % av jokerteckenanteckningarna direkt kunde ha ersatts av anteckningar på deklarationsplatsen. De återstående 61 % är alltså en indikation på platser där Java drar nytta av att ha användningsplatssystemet tillgängligt.
I ett deklarationsplatsspråk måste biblioteken antingen exponera mindre varians eller definiera fler gränssnitt. Till exempel definierar biblioteket Scala Collections tre separata gränssnitt för klasser som använder kovarians: ett kovariansbasgränssnitt som innehåller vanliga metoder, en oföränderlig föränderlig version som lägger till sidoverkande metoder och en kovariant oföränderlig version som kan specialisera de ärvda implementeringarna för att utnyttja strukturella delning. Denna design fungerar bra med deklarationsplatskommentarer, men det stora antalet gränssnitt medför en komplexitetskostnad för bibliotekets klienter. Och att modifiera biblioteksgränssnittet kanske inte är ett alternativ – i synnerhet var ett mål när man lade till generika till Java att bibehålla binär bakåtkompatibilitet.
Å andra sidan är Java jokertecken i sig komplexa. I en konferenspresentation Joshua Bloch dem för att vara för svåra att förstå och använda och påstod att när vi lägger till stöd för stängningar "har vi helt enkelt inte råd med ytterligare jokertecken ". Tidiga versioner av Scala använde variansanteckningar för användningsplats, men programmerare tyckte att de var svåra att använda i praktiken, medan annoteringar för deklarationsplats visade sig vara till stor hjälp vid utformningen av klasser. Senare versioner av Scala lade till existentiella typer och jokertecken i Java-stil; men enligt Martin Odersky , om det inte fanns något behov av interoperabilitet med Java skulle dessa förmodligen inte ha inkluderats.
Ross Tate hävdar att en del av komplexiteten hos Java-jokertecken beror på beslutet att koda användningsplatsvarians med hjälp av en form av existentiella typer. De ursprungliga förslagen använde specialsyntax för varianskommentarer och skrev List <+ Animal > istället för Javas mer utförliga Lista <? sträcker sig Djur > .
Eftersom jokertecken är en form av existentiella typer kan de användas till fler saker än bara varians. En typ som List <?> ("en lista av okänd typ") låter objekt skickas till metoder eller lagras i fält utan att exakt specificera deras typparametrar. Detta är särskilt värdefullt för klasser som Class där de flesta av metoderna inte nämner typparametern.
Typinferens för existentiella typer är dock ett svårt problem. För kompilatorimplementeraren väcker Java-jokertecken problem med typkontrollavslutning, typargumentslutning och tvetydiga program. I allmänhet är det oklart om ett Java-program som använder generika är välskrivet eller inte, så vilken typkontroll som helst måste gå in i en oändlig loop eller timeout för vissa program. För programmeraren leder det till komplicerade felmeddelanden. Java-typ kontrollerar jokerteckentyper genom att ersätta jokertecken med färska typvariabler (så kallad capture conversion ) . Detta kan göra felmeddelanden svårare att läsa, eftersom de refererar till typvariabler som programmeraren inte direkt skrev. Om du till exempel försöker lägga till en katt på en lista <? förlänger Animal > kommer att ge ett fel som
metod List.add (capture#1) är inte tillämplig (faktiskt argument Cat kan inte konverteras till capture#1 genom metodanropsomvandling) där capture#1 är en ny typvariabel: capture#1 utökar Animal from capture of ? sträcker sig Animal
Eftersom både deklarationsplats- och användningsplatsannoteringar kan vara användbara, tillhandahåller vissa typsystem båda.
Etymologi
Dessa termer kommer från begreppet kovarianta och kontravarianta funktioner i kategoriteorin . Betrakta kategorin vars objekt är typer och vars morfismer representerar subtyprelationen ≤. (Detta är ett exempel på hur vilken som helst partiellt ordnad mängd kan betraktas som en kategori.) Sedan tar till exempel funktionstypens konstruktor två typer p och r och skapar en ny typ p → r ; så det tar objekt i till objekt i . Genom subtypningsregeln för funktionstyper omvänder denna operation ≤ för den första parametern och bevarar den för den andra, så det är en kontravariant funktion i den första parametern och en kovariansfunktion i den andra.
Se även
-
^ Detta händer bara i ett patologiskt fall. Skriv till exempel
'at = int: vilken typ som helst kan läggas in för'aoch resultatet är fortfarandeint[ förtydligande behövs ] - ^ Func<T, TResult> Delegat - MSDN-dokumentation
- ^ Reynolds, John C. (1981). Essensen av Algol . Symposium om algoritmiska språk. Nord-Holland.
-
^
Cardelli, Luca (1984). En semantik av multipelt arv (PDF) . Semantics of Data Types (International Symposium Sophia-Antipolis, Frankrike, 27–29 juni 1984). Föreläsningsanteckningar i datavetenskap. Vol. 173. Springer. s. 51–67. doi : 10.1007/3-540-13346-1_2 . ISBN 3-540-13346-1 . Längre version: — (februari 1988). "En semantik av multipelt arv". Information och beräkning . 76 (2/3): 138–164. CiteSeerX 10.1.1.116.1298 . doi : 10.1016/0890-5401(88)90007-7 . - ^ Torgersen, Mads. "C# 9.0 på posten" .
- ^ Allison, Chuck. "Vad är nytt i Standard C++?" .
- ^ "Att fixa vanliga typproblem" . Dart programmeringsspråk .
- ^ Bertrand Meyer (oktober 1995). "Statisk typning" (PDF) . OOPSLA 95 (Objektorienterad programmering, system, språk och applikationer), Atlanta, 1995 .
- ^ a b Howard, Mark; Bezault, Eric; Meyer, Bertrand; Colnet, Dominique; Stapf, Emmanuel; Arnout, Karine; Keller, Markus (april 2003). "Typsäker kovarians: Kompetenta kompilatorer kan fånga alla catcalls" (PDF) . Hämtad 23 maj 2013 .
- ^ Franz Weber (1992). "Att få klassriktighet och systemkorrekthet ekvivalent - hur man får kovarians rätt". TOOLS 8 (8:e konferensen om teknologi för objektorienterade språk och system), Dortmund, 1992 . CiteSeerX 10.1.1.52.7872 .
- ^ Castagna, Giuseppe (maj 1995). "Kovarians och kontravarians: konflikt utan orsak". ACM-transaktioner på programmeringsspråk och system . 17 (3): 431–447. CiteSeerX 10.1.1.115.5992 . doi : 10.1145/203095.203096 . S2CID 15402223 .
- ^ Lippert, Eric (3 december 2009). "Exakta regler för variansvaliditet" . Hämtad 16 augusti 2016 .
- ^ "Avsnitt II.9.7". ECMA International Standard ECMA-335 Common Language Infrastructure (CLI) (6:e upplagan). juni 2012.
-
^ a b c
Altidor, John; Shan, Huang Shan; Smaragdakis, Yannis (2011). "Tämja jokertecken: kombinera definition- och användningsplatsvarians". Proceedings från den 32:a ACM SIGPLAN-konferensen om programmeringsspråksdesign och implementering (PLDI'11) . ACM. s. 602–613. CiteSeerX 10.1.1.225.8265 . doi : 10.1145/1993316.1993569 . ISBN 9781450306638 .
{{ citera konferens }}: CS1 underhåll: datum och år ( länk ) - ^ Lippert, Eric (29 oktober 2007). "Kovarians och kontravarians i C# del sju: Varför behöver vi överhuvudtaget en syntax?" . Hämtad 16 augusti 2016 .
- ^ Odersky, Marin; Spoon, Lex (7 september 2010). "Scala 2.8 Collections API" . Hämtad 16 augusti 2016 .
-
^
Bloch, Joshua (november 2007). "The Closures Controversy [video]" . Presentation på Javapolis'07. Arkiverad från originalet 2014-02-02.
{{ citera webben }}: CS1 underhåll: plats ( länk ) - ^ Odersky, Martin; Zenger, Matthias (2005). "Skalbara komponentabstraktioner" (PDF) . Proceedings från den 20:e årliga ACM SIGPLAN-konferensen om objektorienterad programmering, system, språk och applikationer (OOPSLA '05) . ACM. s. 41–57. CiteSeerX 10.1.1.176.5313 . doi : 10.1145/1094811.1094815 . ISBN 1595930310 .
- ^ Venners, Bill; Sommers, Frank (18 maj 2009). "Syftet med Scalas typsystem: En konversation med Martin Odersky, del III" . Hämtad 16 augusti 2016 .
- ^ a b Tate, Ross (2013). "Mixed-site Variance" . FOOL '13: Informella förfaranden för den 20:e internationella workshopen om grunderna för objektorienterade språk . CiteSeerX 10.1.1.353.4691 .
- ^ Igarashi, Atsushi; Viroli, Mirko (2002). "Om variansbaserad undertypning för parametriska typer". Handlingar från den 16:e europeiska konferensen om objektorienterad programmering (ECOOP '02) . Föreläsningsanteckningar i datavetenskap. Vol. 2374. s. 441–469. CiteSeerX 10.1.1.66.450 . doi : 10.1007/3-540-47993-7_19 . ISBN 3-540-47993-7 .
-
^
Thorup, Kresten Krab; Torgersen, Mads (1999). "Förenande genericitet: Kombinera fördelarna med virtuella typer och parametriserade klasser". Objektorienterad programmering (ECOOP '99) . Föreläsningsanteckningar i datavetenskap. Vol. 1628. Springer. s. 186–204. CiteSeerX 10.1.1.91.9795 . doi : 10.1007/3-540-48743-3_9 . ISBN 3-540-48743-3 .
{{ citera konferens }}: CS1 underhåll: datum och år ( länk ) - ^ "The Java™ Tutorials, Generics (Uppdaterade), Unbounded Wildcards" . Hämtad 17 juli 2020 .
- ^ Tate, Ross; Leung, Alan; Lerner, Sorin (2011). "Tämja jokertecken i Javas typsystem" . Proceedings från den 32:a ACM SIGPLAN-konferensen om programmeringsspråksdesign och implementering (PLDI '11) . s. 614–627. CiteSeerX 10.1.1.739.5439 . ISBN 9781450306638 .
- ^ Grigore, Radu (2017). "Java generika är slutförda". Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages (POPL'17) . s. 73–85. arXiv : 1605.05274 . Bibcode : 2016arXiv160505274G . ISBN 9781450346603 .
externa länkar
- Fabulous Adventures in Coding : En artikelserie om implementering handlar om samverkan/kontravarians i C#
- Contra Vs Co Variance (observera att denna artikel inte är uppdaterad om C++)
- Stängningar för programmeringsspråket Java 7 (v0.5)
- Teorin bakom kovarians och kontravarians i C# 4