Kolmogorov-Zurbenko filter

Ej att förväxla med Korkine–Zolotarev gitterbasreduktionsalgoritm .

Inom statistik föreslogs Kolmogorov–Zurbenko (KZ)-filtret först av AN Kolmogorov och definierades formellt av Zurbenko. Det är en serie iterationer av ett glidande medelfilter med längden m , där m är ett positivt, udda heltal. KZ-filtret tillhör klassen lågpassfilter . KZ-filtret har två parametrar, längden m för det glidande medelvärdet och antalet iterationer k av själva det glidande medelvärdet. Det kan också betraktas som en speciell fönsterfunktion utformad för att eliminera spektralläckage.

Andrey Kolmogorov och Igor Zurbenko på ett forskningsfartyg i Stilla havet.

Bakgrund

AN Kolmogorov hade den ursprungliga idén till KZ-filtret under en studie av turbulens i Stilla havet. Kolmogorov hade precis fått det internationella Balzanpriset för sin lag om 5/3 i turbulensens energispektra . Överraskande nog följdes inte 5/3-lagen i Stilla havet, vilket orsakade stor oro. Standard snabb Fourier-transform (FFT) blev helt lurad av den bullriga och icke-stationära havsmiljön. KZ-filtrering löste problemet och möjliggjorde bevis för Kolmogorovs lag på den domänen. Filterkonstruktionen förlitade sig på huvudkoncepten för den kontinuerliga Fouriertransformen och deras diskreta analoger. Algoritmen för KZ-filtret kom från definitionen av högre ordningens derivator för diskreta funktioner som högre ordningens skillnader . Eftersom Kolmogorov trodde att oändlig jämnhet i det Gaussiska fönstret var en vacker men orealistisk approximation av en verkligt diskret värld, valde Kolmogorov ett ändligt differentierbart avsmalnande fönster med ändligt stöd och skapade denna matematiska konstruktion för det diskreta fallet. KZ-filtret är robust och nästan optimalt. Eftersom dess funktion är ett enkelt glidande medelvärde (MA), presterar KZ-filtret bra i en saknad datamiljö, särskilt i flerdimensionella tidsserier där problem med saknade data uppstår på grund av spatial gleshet. En annan trevlig egenskap hos KZ-filtret är att de två parametrarna har en tydlig tolkning så att den lätt kan antas av specialister inom olika områden. Ett fåtal mjukvarupaket för tidsserier, longitudinella och rumsliga data har utvecklats i den populära statistiska programvaran R, som underlättar användningen av KZ-filtret och dess tillägg inom olika områden. I.Zurbenko Postdoktor vid UC Berkeley med Jerzy Neyman och Elizabeth Scott gav många idéer om applikationer som stöddes i kontakter med Murray Rosenblatt , Robert Shumway, Harald Cramér , David Brillinger, Herbert Robbins , Wilfrid Dixon , Emanuel Parzen .

Definition

KZ filter

Låt $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ vara ett verkligt värde tidsserier , KZ-filtret med parametrarna $m$ och $k$ definieras som

$KZ_{m ,k}[X(t)]=\summa _{s=-k(m-1)/2}^{k(m-1)/2}{X(t+s)\ gånger {a_{s }^{m,k}}}$

där koefficienter

$a_{s}^{m,k}={\ frac {c_{s}^{k,m}}{m^{k}}},s={\frac {-k(m-1)}{2}},\dots ,{\frac {k( m-1)}{2}}$

ges av polynomkoefficienterna som erhålls från ekvationen

$\sum _{r=0} ^{k(m-1)}{z^{r}c_{rk(m-1)/2}^{k,m}=(1+z+\dots +z^{m-1})^{ k}}$

Ur en annan synvinkel kan KZ-filtret med parametrarna $m$ och $k$ definieras som $k$ -tidsiterationer av ett glidande medelvärde (MA)-filter av $m$ poäng. Det kan erhållas genom iterationer.

Första iterationen är att applicera ett MA-filter över process $X(t)$

$KZ_{m,k= 1}[X(t)]=\summa _{s=-(m-1)/2}^{(m-1)/2}{X(t+s)}\ gånger {\frac {1} {m}}$

Den andra iterationen är att tillämpa MA-operationen på resultatet av den första iterationen,

${\begin{aligned}&KZ_{m,k= 2}[X(t)]=\summa _{s=-(m-1)/2}^{(m-1)/2}{KZ_{m,k=1}[X(t+s) ]\ gånger {\frac {1}{m}}}\\={}&\sum _{s=-2(m-1)/2}^{2(m-1)/2}{X( t+s)\ gånger {a_{s}^{m,k=2}}}\end{aligned}}$

Generellt är den k: te iterationen en tillämpning av MA-filtret på ( k − 1):e iterationen. Iterationsprocessen för en enkel operation av MA är mycket bekväm beräkningsmässigt.

Egenskaper

Impulssvarsfunktionen för produkten av filter är faltningen av impulssvar. Koefficienterna för KZ-filtret a
^{m , k} _s , kan tolkas som en fördelning som erhålls genom faltningen av k enhetliga diskreta fördelningar på intervallet [ −( m − 1)/2 , ( m − 1)/2 ] där m är ett udda heltal. Därför bildar koefficienten a ett
avsmalnande fönster som har ändligt stöd [ ( m − 1) k + 1] . KZ-filtret a
har huvudvikten koncentrerad till en längd av m √ k med vikter som försvinner till noll utanför. KZ-filtrets impulssvarsfunktion har k − 2 kontinuerliga derivator och är asymptotiskt Gaussfördelad. Nollderivator vid kanterna för impulssvarsfunktionen gör från den till en kraftigt avtagande funktion, det som löser upp i högfrekvent upplösning. Energiöverföringsfunktionen för KZ-filtret är

$|B_{m,k}(\omega )|^{2}=\left\{{\frac {1}{m}}{\frac {\sin(\pi m\omega )}{\ sin(\pi \omega )}}\right\}^{2k}.$

Det är ett lågpassfilter med en gränsfrekvens på

$\omega _{0}\approx {\frac {\sqrt {6}}{\pi }}{\sqrt {\frac {1-(1/2)^{1/2k}}{m^ {2}-(1/2)^{1/2k}}}}.$

Figur 1. Överföringsfunktion för filter för k = 1.

Jämfört med ett MA-filter har KZ-filtret mycket bättre prestanda när det gäller att dämpa frekvenskomponenterna över cutoff-frekvensen. KZ-filtret är i huvudsak ett repetitivt MA-filter. Det är lätt att beräkna och möjliggör ett enkelt sätt att hantera saknad data. Huvuddelen av denna procedur är ett enkelt medelvärde av tillgänglig information inom intervallet m punkter utan hänsyn till de saknade observationerna inom intervallet. Samma idé kan enkelt utvidgas till rumslig dataanalys. Det har visat sig att saknade värden har mycket liten effekt på KZ-filtrets överföringsfunktion.

Godtycklig k kommer att tillhandahålla k- effekt för denna överföringsfunktion och kommer att reducera sidolobsvärdet till 0,05 ^k . Det blir ett perfekt lågpassfilter. För praktiska ändamål är ett val av k inom ett område 3 till 5 vanligtvis tillräckligt, när vanlig MA ( k = 1) ger ett starkt spektralläckage på cirka 5%.

Optimalitet

KZ-filtret är robust och nästan optimalt. Eftersom dess funktion är ett enkelt glidande medelvärde, fungerar KZ-filtret bra i en saknad datamiljö, särskilt i flerdimensionell tid och rum där saknad data kan orsaka problem som uppstår på grund av spatial gleshet. En annan trevlig egenskap hos KZ-filtret är att de två parametrarna var och en har tydliga tolkningar så att de enkelt kan antas av specialister inom olika områden. Mjukvaruimplementationer för tidsserier, longitudinella och rumsliga data har utvecklats i det populära statistiska paketet R , vilket underlättar användningen av KZ-filtret och dess tillägg inom olika områden.

KZ-filter kan användas för att jämna ut periodogrammet . För en klass av stokastiska processer ansåg Zurbenko det värsta scenariot där den enda information som finns tillgänglig om en process är dess spektrala täthet och jämnhet kvantifierad av Hölders tillstånd . Han härledde den optimala bandbredden för det spektrala fönstret, vilket är beroende av den underliggande jämnheten hos den spektrala tätheten. Zurbenko jämförde prestandan för Kolmogorov-Zurbenko (KZ) fönster med de andra typiskt använda spektralfönstren inklusive Bartlett-fönster , Parzen-fönster , Tukey-Hamming-fönster och enhetligt fönster och visade att resultatet från KZ-fönster är närmast optimalt.

Utvecklad som en abstrakt diskret konstruktion, KZ-filtrering är robust och statistiskt nästan optimal. Samtidigt, på grund av sin naturliga form, har den beräkningsmässiga fördelar, vilket möjliggör analys av rum/tidsproblem med data som saknar mycket som 90% av observationerna, och som representerar en rörig kombination av flera olika fysiska fenomen. Tydliga svar kan ofta hittas för "olösliga" problem. Till skillnad från vissa matematiska utvecklingar är KZ anpassningsbar av specialister inom olika områden eftersom den har en tydlig fysisk tolkning bakom sig.

Tillägg

Figur 2: Logaritm för överföringsfunktionen för KZFT _{m , k} -filtret med ₀ ν = .04, m = 100 och k = 1 (svart) eller k = 5 (röd).

Figur 3: Spektrum för signalen som är summeringen av två sinusvågor om frekvenserna 0,08 och 0,10 cykler per tidsenhet plus brus N(0,16) med 70 % saknade värden. Adaptivt utjämnad KZP-algoritm användes för att bestämma spektrumet för den simulerade datamängden.

Figur 4: Den rekonstruerade signalen som är summan av två sinusvågor om frekvenserna 0,08 och 0,10 cykler per tidsenhet från en originalsignal med tillagt brus ~N(0, 16) och där 60% av värdena inte var tillgängliga.

Utvidgningar av KZ-filter inkluderar KZ-adaptivt (KZA)-filter, spatialt KZ-filter och KZ Fourier-transform (KZFT). Yang och Zurbenko gav en detaljerad genomgång av KZ-filtret och dess tillägg. R-paket finns också tillgängliga för att implementera KZ-filtrering

KZFT

KZFT-filtret är designat för en rekonstruktion av periodiska signaler eller säsongsvariationer som täcks av kraftigt brus. Säsongsvariation är en av nyckelformerna av icke-stationaritet som ofta ses i tidsserier. Det definieras vanligtvis som de periodiska komponenterna inom tidsserien. Spektralanalys är ett kraftfullt verktyg för att analysera tidsserier med säsongsvariationer. Om en process är stationär är dess spektrum också en kontinuerlig form. Det kan behandlas parametriskt för att förenkla förutsägelsen. Om ett spektrum innehåller linjer indikerar det att processen inte är stationär och innehåller periodiciteter. I denna situation resulterar parametrisk anpassning i allmänhet i säsongsrester med reducerad energi. Detta beror på säsong till säsong variationer. För att undvika detta problem rekommenderas icke-parametriska metoder inklusive bandpassfilter. Kolmogorov–Zurbenko Fourier Transform (KZFT) är ett av sådana filter. Syftet med många applikationer är att rekonstruera högupplöst wavelet från den bullriga miljön. Det bevisades att KZFT ger bästa möjliga upplösning i spektral domän. Den tillåter separering av två signaler på kanten av ett teoretiskt minsta avstånd, eller rekonstruerar periodiska signaler täckta av kraftigt brus och oregelbundet observerade i tid. På grund av detta ger KZFT en unik möjlighet för olika applikationer. En datoralgoritm för att implementera KZFT har tillhandahållits i R-programvaran. KZFT är i huvudsak ett bandpassfilter som tillhör kategorin korttids Fourier-transform (STFT) med ett unikt tidsfönster.

KZFT upptäcker lätt små avvikelser från en konstant spektral densitet av vitt brus som härrör från datorns slumptalsgenerator . Sådana datorgenerationer med slumptal blir förutsägbara på lång sikt. Kolmogorovs komplexitet ger möjlighet att generera oförutsägbara sekvenser av slumptal.

₀ Formellt har vi en process X ( t ) , t = ...,−1,0,1,... , KZFT-filtret med parametrarna m och k , beräknat vid frekvensen ν , producerar en utgångsprocess, som är definierad enligt följande:

$KZFT_{m,k,\nu _{0}}[X(t)]=\summa _{s=-k(m-1)/2}^{k (m-1)/2}{X(t+s)\ gånger {a_{s}^{m,k}\ gånger {e^{-i(2m\nu _{0})s}}}}$

där a
^{m , k} _s definieras som: a
^{m , k} _s = C
^{m , k} _s / m ^k , s = −k(m − 1) / 2 ,..., −k(m − 1) / 2 och polynomkoefficienterna C
^{m , k} _s ges av Σ
^{k ( m − 1)} _{r = 0} z ^r C
^k,m _{r − k ( m − 1)/2} = (1 + z + ... + z ^{( m − 1)} ) ^k . Tydligen KZFT
_{m,k,ν 0} (t) [ X ( t )] filter ekvivalent med tillämpningen av KZFT
_m,k ( t ) filter på processen X ( t + s ) e ^{₀ − i2 ( mν ) s} . På samma sätt kan KZFT-filtret erhållas genom iterationer på samma sätt som KZ-filtret.

₀₀ Genomsnittet av kvadraten av KZFT i tid över S perioder av ₀ ρ = 1 / ν ₀ kommer att ge en uppskattning av kvadratamplituden för vågen vid frekvensen ν eller KZ periodogram (KZP) baserat på 2 Sρ -observationer runt ögonblicket t :

$\operatörsnamn {KZP} (t,m,k,\nu _{0})=2\vänster|{\frac {1}{2S\rho _{0}}}\summa _{\tau = -S\rho _{0}}^{S\rho _{0}}2\operatörsnamn {Re} [KZFT_{m,k,\nu +0}[X(\tau +t)]]^{2 }\right|$

₀₀₀ c /( m√k Överföringsfunktionen för KZFT tillhandahålls ) i figur 2 har en mycket skarp frekvensupplösning med bandbredd begränsad av . För en process med komplext värde är X ( t ) = ei ^{₀ (2mν )t} , KZFT _{-m,k,ν 0} ( t ) -utfallet oförändrat. För en verkligt värderad process fördelar den energin jämnt över de verkliga och komplexa domänerna. Med andra ord, 2Re[ KZFT _{m,k,ν 0} ( t )] rekonstruerar en cosinus- eller sinusvåg med samma frekvens ν . Det följer att 2Re[ KZFT _{m,k,ν 0} ( t )] korrekt rekonstruerar amplituden och fasen för en okänd våg med frekvensen ν . Bilden nedan visar kraftöverföringsfunktionen för KZFT-filtrering. Den visar tydligt att den perfekt fångade den intressanta frekvensen ν = 0,4 och ger praktiskt taget inget spektralläckage från en sidolober som styr genom parametern k för filtrering. För praktiska ändamål är valet av k inom intervallet 3–5 vanligtvis tillräckligt, när vanlig FFT ( k = 1) ger ett starkt läckage på cirka 5 %.

Exempel: Simulerad signal sin 2π(0,10) t + sin 2 π (0,02) t + normalt slumpmässigt brus N(0,16) användes för att testa KZFT-algoritmens förmåga att exakt bestämma spektra av datamängder med saknade värden. Av praktiska skäl användes procentandelen saknade värden vid p=70 % för att bestämma om spektrumet kunde fortsätta att fånga de dominerande frekvenserna. Med hjälp av en bredare fönsterlängd på m=600 och k=3 iterationer användes adaptivt utjämnad KZP-algoritm för att bestämma spektrumet för den simulerade longitudinella datamängden. Det är uppenbart i figur 3 att de dominanta frekvenserna på 0,08 och 0,10 cykler per tidsenhet är identifierbara som signalens inneboende frekvenser.

KZFT-rekonstruktion av originalsignal inbäddad i det höga bruset från longitudinella observationer (saknadsfrekvens 60%). KZFT-filtret i KZA-paketet av R-programvara har en parameter f = frekvens . Genom att definiera denna parameter för var och en av de kända dominanta frekvenserna som finns i spektrumet, filter KZFT med parametrarna m=300 och k=3 för att rekonstruera signalen om varje frekvens (0,08 och 0,10 cykler per tidsenhet). Den rekonstruerade signalen bestämdes genom att applicera KZFT-filtret två gånger (en gång om varje dominant frekvens) och sedan summera resultaten av varje filter. Korrelationen mellan den sanna signalen och den rekonstruerade signalen var 96,4 %; visas i figur 4. De ursprungliga observationerna ger ingen gissning om den komplexa, dolda periodiciteten, som rekonstruerades perfekt av algoritmen.

Rådata innehåller ofta dolda frekvenser. Kombinationer av ett fåtal vågor med fast frekvens kan komplicera igenkännandet av blandningen av signaler, men förbli förutsägbara över tiden. Publikationer visar att atmosfärstryck innehåller dolda periodiciteter som härrör från månens gravitationskraft och solens dagliga period. Rekonstruktionen av dessa periodiska signaler från atmosfäriska flodvågor möjliggör en förklaring och förutsägelse av många anomalier som finns i extremt väder. Liknande flodvågor måste existera på solen till följd av planeternas gravitationskraft. Solens rotation runt dess axlar kommer att orsaka en ström, liknande den ekvatoriska strömmen på jorden. Störningar eller virvlar runt strömmen kommer att orsaka anomalier på solens yta. Horisontella roterande virvlar i högmagnetisk plasma kommer att skapa en vertikal explosion som kommer att transportera djupare, hetare plasma till ovanför solens yta. Varje planet skapar en flodvåg med en specifik frekvens på solen. Ibland kommer två av vågorna att inträffa i fas och andra tider kommer att vara ur fas. Den resulterande amplituden kommer att oscillera med en skillnadsfrekvens. Uppskattningen av spektra av solfläcksdata med hjälp av DZ-algoritmen ger två skarpa frekvenslinjer med periodicitet nära 9,9 och 11,7 år. Dessa frekvenslinjer kan betraktas som skillnadsfrekvenser orsakade av Jupiter och Saturnus (9,9) och Venus och jorden (11,7). Skillnadsfrekvensen mellan 9,9 och 11,7 ger en frekvens med en 64-årsperiod. Alla dessa perioder är identifierbara i solfläcksdata. 64-årsperioden är för närvarande i ett sjunkande läge. Denna nedgång kan orsaka en kylande effekt på jorden inom en snar framtid. En undersökning av den gemensamma effekten av flera planeter kan avslöja några långa perioder i solens aktivitet och hjälpa till att förklara klimatfluktuationer på jorden.

KZA

Figur 5a: Plot av signal + säsongsvariationer + brus. Figur 5b: KZA-rekonstruktion av signalen med brytningen från data i figur 5a. Blå linje är rekonstruktion av originalsignalen som en svart linje.

Figur 6: Tillämpning av KZFT _{m , k} på data i figur 5a. Ett vanligt lågpassfilter kan inte reproducera avbrottet på lång sikt.

Adaptiv version av KZ-filtret, kallat KZ adaptivt (KZA)-filter, utvecklades för att söka efter avbrott i icke-parametriska signaler som täcks av kraftigt brus. KZA-filtret identifierar först potentiella tidsintervall när ett avbrott inträffar. Den undersöker sedan dessa tidsintervall mer noggrant genom att minska fönsterstorleken så att upplösningen för det utjämnade resultatet ökar.

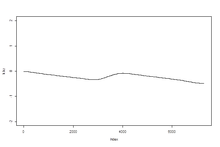
Som ett exempel på brytpunktsdetektering simulerar vi en långsiktig trend som innehåller ett avbrott begravt i säsongsvariationer och buller. Figur 2 är en kurva över en säsongsbetonad sinusvåg med amplituden 1 enhet, normalfördelat brus ( σ = 1 ), och en bassignal med ett avbrott. För att göra saker mer utmanande innehåller bassignalen en övergripande nedåtgående trend på 1 enhet och en uppåtgående brytning på 0,5 enheter. Den nedåtgående trenden och brottet syns knappt i originaldata. Bassignalen är en stegfunktion y = −1 / 7300 t + sin(2 π t ) , med t < 3452 och y = −1 / 7300 ( t − 3452) + sin(2 π t ) med 3452 < t < 7300 . Tillämpningen av ett lågpassutjämningsfilter KZ _{3 365} på originaldata resulterar i en överutjämning av brottet såsom visas i figur 6. Avbrottets läge är inte längre uppenbart. Tillämpningen av en adaptiv version av KZ-filtret (KZA) hittar brytningen som visas i figur 5b. Konstruktionen av KZA är baserad på en adaptiv version av det itererade utjämningsfiltret KZ. Tanken är att ändra storleken på filtreringsfönstret baserat på trenderna som hittas med KZ. Detta gör att filtret zoomar in på de områden där data ändras; Ju snabbare ändringen är, desto snävare blir zoomen. Det första steget i att konstruera KZA är att använda KZ; KZ _{q , k} [ X ( t )] där k är iterationer och q är filterlängden, där KZ _{q , k} är ett itererat glidande medelvärde y _i = 1 / (2 q +1) Σ
^q _j=-q X _{i + j} där x _i är originaldata och y _i är filtrerade data. Detta resultat används för att bygga en adaptiv version av filtret. Filtret är sammansatt av ett huvud och en svans ( qf respektive qb ), med f = huvud och b = svans) som anpassar sig i storlek som svar på data, vilket effektivt zoomar in på regioner där data förändras _{snabbt .} Huvudet qf _krymper som svar på avbrottet i data. Skillnadsvektorn byggd från KZ; D ( t ) = | Z ( t + q ) - Z ( t - q ) | används för att hitta den diskreta ekvivalenten till derivatan D ' ( t ) = D ( t + 1) − D ( t ) . _{Detta resultat} bestämmer storleken på huvudet och svansen ( qf respektive qb ) av filtreringsfönstret. Om lutningen är positiv kommer huvudet att krympa och svansen expanderar till full storlek ( D qf ( t ) = _f ( D ( t )) q ' ( t ) > 0 , qb ( _t ) = q då och ) med f ( D ( t )) = 1- D ( t ) / max[ D ( t )] . Om lutningen är negativ kommer fönstrets huvud att ha full storlek medan svansen kommer att krympa ( _D qf ( t )= q ' ( t ) < 0 , qb ( _t )= f ( D ( t )) q sedan och . Detaljerad kod för KZA är tillgänglig.

Figur 7: Rekonstruktion av kvadratisk bild av den 2-dimensionella signalen på nivå 1 begravd i det normala bruset med σ=2. Vänster är brusig bild, höger är applicering av 2-dimensionell KZA. Totalt visningsfält är 100x100 punkter, originalbilden är 30x30 i mitten.

KZA-algoritmen har alla de typiska fördelarna med ett icke-parametriskt tillvägagångssätt; det kräver ingen specifik modell av tidsserien som undersöks. Den söker efter plötsliga förändringar över en lågfrekvent signal av vilken typ som helst som täcks av kraftigt brus. KZA visar mycket hög känslighet för avbrottsdetektering, även med ett mycket lågt signal-brusförhållande; noggrannheten i detekteringen av tidpunkten för pausen är också mycket hög.

KZA-algoritmen kan användas för att återställa brusiga tvådimensionella bilder. Detta kan vara en tvånivåfunktion f(x,y) som en svartvit bild skadad av starkt brus, eller en flernivåfärgbild. KZA kan appliceras rad för rad för att upptäcka brytningen (färgförändring), sedan skulle brytpunkterna vid olika linjer jämnas ut av det vanliga KZ-filtret. Demonstration av rumslig KZA ges i figur 7.

Bestämningar av skarpa frekvenslinjer i spektra kan bestämmas genom adaptivt utjämnat periodogram. Den centrala idén med algoritmen är att adaptivt jämna ut logaritmen för ett KZ-periodogram. Utjämningsintervallet tillhandahålls av någon fast procentandel av villkorlig entropi från total entropi . Grovt sett fungerar algoritmen enhetligt på en informationsskala snarare än en frekvensskala. Denna algoritm är också känd för parametern k=1 i KZP som Dirienzo-Zurbenko-algoritmen och tillhandahålls i programvara.

Rumsligt KZ-filter

Spatial KZ-filter kan appliceras på variabeln registrerad i tid och rum. Filtrets parametrar kan väljas separat i tid och rum. Vanligtvis kan fysisk känsla tillämpas vilken skala av medelvärde som är rimlig i rymden och vilken skala av medelvärde som är rimlig i tid. Parameter k styr skärpan i filtrets upplösning eller undertryckning av läckage av frekvenser. En algoritm för spatialt KZ-filter finns i R-programvaran. Resultattidsparameter kan behandlas som virtuell tid, sedan kan bilder av resultat av filtrering i rymden visas som "film" i virtuell tid. Vi kan demonstrera tillämpningen av 3D-spatialt KZ-filter applicerat på världsrekorden av temperatur T ( t , x , y ) som en funktion av tid t , longitud x och latitud y . För att välja globala klimatfluktuationer valdes komponentparametrar 25 månader för tid t , 3° för longitud och latitud för KZ-filtrering. Parametern k valdes lika med 5 för att tillgodose skalupplösningar. En bild av resultatet "film" visas i figur 8 nedan. Standard genomsnittlig cosinus kvadrat temperaturfördelning låg längs breddgrader subtraherades för att identifiera fluktuationer i klimatet i tid och rum.

Figur 8: Global långtidskomponent i december 2007 KZ-filter m = (3°, 3°, 25 månader), k = 5, justerat för latitud- och höjdeffekter.

Vi kan se anomalier av temperaturfluktuationer från cosinuskvadratlag över jordklotet för 2007. Temperaturavvikelser visas över jordklotet i den angivna figurskalan till höger. Den visar mycket positiva anomalier över Europa och Nordafrika, som sträckte sig över de senaste 100 åren. Variabeln med absolut luftfuktighet håller ansvaret för stora regionala klimatförändringar som den nyligen visades av Zurbenko Igor och Smith Devin i Kolmogorov-Zurbenko-filter i rumslig tidsanalys. Dessa anomalier förändras långsamt i tiden i resultatet "filmen" av KZ-filtrering, långsam intensifiering av observerade anomalier identifierades i tid. Olika skalfluktuationer som El Niño-skala och andra kan också identifieras genom rumslig KZ-filtrering. Högupplösta "filmer" av dessa skalor finns över Nordamerika. Olika skalor kan väljas genom KZ-filtrering för en annan variabel och motsvarande multivariatanalys kan ge högeffektiva resultat för att undersöka utfallsvariabel över andra kovariater. KZ-filterupplösningen presterar exceptionellt bra jämfört med konventionella metoder och är faktiskt beräkningsmässigt optimal.

Genomföranden

• W. Yang och I. Zurbenko. kzft: Kolmogorov–Zurbenko Fourier transformation och tillämpning. R-paket, 2006.
• B. Close och I. Zurbenko. kza: Kolmogorov–Zurbenko adaptiv algoritm för bilddetektering. R-paket, 2016 ( https://cran.r-project.org/web/packages/kza/ )
• KZ och KZA Java-implementering för 1-dimensionella arrayer av Andreas Weiler och Michael Grossniklaus (University of Konstanz, Tyskland) ( https://web.archive.org/web/20140914054417/http://dbis.uni-konstanz.de/ forskning/social-media-stream-analys/ )
• Python-implementering av KZ, KZFT och KZP av Mathieu Schopfer (University of Lausanne, Schweiz) ( https://github.com/MathieuSchopfer/kolmogorov-zurbenko-filter )