Kolinearitetsekvation

Ljusstrålar som passerar genom hålet på en hålkamera

Kollinearitetsekvationerna är en uppsättning av två ekvationer, som används i fotogrammetri och datorstereoseende , för att relatera koordinater i ett sensorplan (i två dimensioner ) till objektkoordinater (i tre dimensioner). Ekvationerna härrör från den centrala projektionen av en punkt på objektet genom kamerans optiska centrum till bilden på sensorplanet.

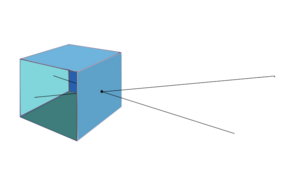
De tre punkterna P, Q och R projiceras på planet S genom projektionscentrum C

x- och z-axeln för projektionen av P genom projektionscentrum C

Definition

Låt x, y och z hänvisa till ett koordinatsystem med x- och y-axeln i sensorplanet. Beteckna koordinaterna för punkten P på objektet med ${\displaystyle x_{P},y_{P},z_{P}} ,$ koordinaterna för bildpunkten för P på sensorplanet av x och y och koordinaterna för projektions (optiskt) centrum med $x_{0},y_{0},z_{0}$ . Som en konsekvens av projektionsmetoden finns det samma fasta förhållande $\lambda$ mellan $x-x_{0}$ och $x_{0}-x_{P }$ , $y-y_{0}$ och $y_{0}-y_{P}$ och avståndet från projektionscentrum till sensorplanet ${ \displaystyle z_{0}=c}$ och $z_{P}-z_{0}$ . Därav:

$x-x_{0}=-\lambda (x_{P}-x_{0})$

${ \displaystyle y-y_{0}=-\lambda (y_{P}-y_{0})}$

$c=\lambda (z_{P}-z_{0 }),$

Att lösa för $\lambda$ i den sista ekvationen och skriva in den i de andra ger:

$x-x_{0}=-c\ {\frac {x_{P}-x_{0}}{z_{P}-z_{0 }}}$

$y-y_{0}=-c\ {\frac {y_{P}-y_{0}}{z_{P} -z_{0}}}$

Punkten P ges normalt i något koordinatsystem "utanför" kameran av koordinaterna X , Y och Z , och projektionscentrum av $X_{0},Y_{0},Z_{0 }$ . Dessa koordinater kan transformeras genom en rotation och en translation till systemet på kameran. Översättningen påverkar inte skillnaderna mellan koordinaterna, och rotationen, ofta kallad kameratransform , ges av en 3×3- matris R , som transformerar $( X-X_{0},Y-Y_{0},Z-Z_{0})$ till:

$x_{P}-x_{0}=R_{11}(X-X_{ 0})+R_{21}(Y-Y_{0})+R_{31}(Z-Z_{0})$

$y_{P}-y_{0}=R_{12}(X-X_{0})+R_{22}(Y-Y_{0})+R_{32 }(Z-Z_{0})$

och

$z_{P}-z_{0}=R_{13}(X-X_{ 0})+R_{23}(Y-Y_{0})+R_{33}(Z-Z_{0})$

Substitution av dessa uttryck leder till en uppsättning av två ekvationer, kända som kollinearitetsekvationer :

$x-x_{0}=-c\ {\frac {R_{11}(X-X_{0})+R_{21}(Y-Y_{0})+R_{31}( Z-Z_{0})}{R_{13}(X-X_{0})+R_{23}(Y-Y_{0})+R_{33}(Z-Z_{0})}}$

$y-y_{0}=-c\ {\frac {R_{12}(X-X_{0})+R_{22}(Y-Y_{0})+R_{32}( Z-Z_{0})}{R_{13}(X-X_{0})+R_{23}(Y-Y_{0})+R_{33}(Z-Z_{0})}}$

Den mest uppenbara användningen av dessa ekvationer är för bilder inspelade med en kamera. I detta fall beskriver ekvationen transformationer från objektrymden (X, Y, Z) till bildkoordinater (x, y). Den ligger till grund för de ekvationer som används vid buntjustering . De indikerar att bildpunkten (på kamerans sensorplatta), den observerade punkten (på objektet) och kamerans projektionscentrum var inriktade när bilden togs.

Se även

• 3D-projektion
• Epipolär geometri
• Pinhole kamera modell