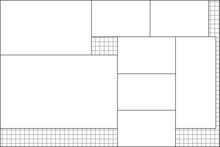
Giljotinpartition

En giljotinskärning: ett optimerat ark av mindre rektanglar som kan delas intakta genom rätt serie av halvskärande snitt från ände till ände.

En icke-giljotinskärning: dessa rektanglar kan inte separeras genom att göra enstaka halvskärande snitt över planet.

Giljotinpartition är processen att dela upp en rätlinjig polygon , som eventuellt innehåller några hål, i rektanglar, med endast giljotinsnitt. Ett giljotinsnitt (även kallat kant-till-kant-snitt ) är en rak halverande linje som går från ena kanten av en befintlig polygon till den motsatta kanten, på samma sätt som en pappers-giljotin .

Giljotinpartition är särskilt vanligt vid design av planlösningar inom mikroelektronik . En alternativ term för en giljotin-partition i detta sammanhang är en skivningsvägg eller en skivande planlösning . Giljotinpartitioner är också den underliggande strukturen för binära rymdpartitioner . Det finns olika optimeringsproblem relaterade till giljotinpartition, såsom: att minimera antalet rektanglar eller den totala längden på snitten. Dessa är varianter av polygonpartitioneringsproblem , där snitten är begränsade till att vara giljotinsnitt.

Ett relaterat men annorlunda problem är giljotinklippning . I det problemet är originalarket en vanlig rektangel utan hål. Utmaningen kommer av att måtten på de små rektanglarna är fixerade i förväg. Optimeringsmålen är vanligtvis att maximera arean av de producerade rektanglarna eller deras värde, eller att minimera avfallet eller antalet ark som krävs.

Beräknar en giljotinpartition med minsta kantlängd

I problemet med minsta kantlängd med rektangulär partition är målet att dela upp den ursprungliga rätlinjiga polygonen i rektanglar, så att den totala kantlängden är ett minimum.

Detta problem kan lösas i tid $O(n^{5})$ även om den råa polygonen har hål. Algoritmen använder dynamisk programmering baserat på följande observation: det finns en minsta längd giljotin-rektangulär partition där varje maximalt linjesegment innehåller en vertex av gränsen . Därför, i varje iteration, finns det $O(n)$ möjliga val för nästa giljotinsnitt, och det finns totalt $O(n^{4})$ underproblem .

I det speciella fallet då alla hål är degenererade (enkla punkter), är den minsta längden rektangulära giljotinväggen högst 2 gånger den minsta längden rektangulära skiljeväggen. Genom en noggrannare analys kan man bevisa att approximationsfaktorn faktiskt är högst 1,75. Det är inte känt om 1,75 är tight, men det finns ett fall där approximationsfaktorn är 1,5. Därför ger giljotinpartitionen en approximation med konstant faktor till det allmänna problemet, som är NP-hårt.

Dessa resultat kan utökas till en d -dimensionell ruta: en giljotinpartition med minsta kantlängd kan hittas i tiden $O(dn^{2d+1})$ , och den totala ( d -1)-volymen i den optimala giljotin-partitionen är som mest $2d-4+4/d$ gånger den för en optimal d -box-partition.

Arora och Mitchell använde giljotinuppdelningstekniken för att utveckla polynom-tidsapproximationsscheman för olika geometriska optimeringsproblem.

Antal giljotinväggar

Förutom beräkningsproblemen studerades giljotinpartitioner också ur ett kombinatoriskt perspektiv. Anta att en given rektangel ska delas upp i mindre rektanglar med endast giljotinsnitt. Uppenbarligen finns det oändligt många sätt att göra detta på, eftersom även ett enda snitt kan ta oändligt många värden. Antalet strukturellt olika giljotinpartitioner är dock begränsat.

• I två dimensioner finns det en övre gräns i $O\left({\frac {n!2^{5n-3}}{n^{3 /2}}}\right)$ tillskriven Knuth . det exakta numret är Schröder-numret .
• I d dimensioner ger Ackerman, Barequet, Pinter och Romik en exakt summeringsformel och bevisar att den är i $\Theta \left({\frac {(2d-1+2{\sqrt {d(d-1)}})^{n}}{n^{3/2}}}\höger)$ . När d =2 blir denna gräns $\Theta \left({\frac {(3+2{\sqrt {2}})^{n}} {n^{3/2}}}\right)$ .
• Asinowski, Barequet, Mansour och Pinter studerar också antalet cut-ekvivalensklasser av giljotinpartitioner.

Färgläggning av giljotinväggar

En polykromatisk färgning av en plan graf är en färgning av dess hörn så att varje färg visas minst en gång i varje yta av grafen. Flera forskare har försökt hitta det största k så att en polykromatisk k -färgning alltid existerar. Ett viktigt specialfall är när grafen representerar en uppdelning av en rektangel i rektanglar.

• Dinitz, Katz och Krakovski bevisade att det alltid finns en polykromatisk 3-färgning.
• Aigner-Horev, Katz, Krakovski och Loffler bevisade att i det speciella underfallet där grafen representerar en giljotinpartition , finns det alltid en stark polykromatisk 4-färgning.
• Keszegh utökade detta resultat till d -dimensionella giljotinpartitioner och gav en effektiv färgalgoritm.
• Dimitrov, Aigner-Horev och Krakovski bevisade slutligen att det alltid finns en stark polykromatisk 4-färgning.

Se även

• Binär rymduppdelning