Gängat binärt träd
Inom beräkningar är ett gängat binärt träd en binär trädvariant som underlättar traversering i en viss ordning (ofta samma ordning som redan har definierats för trädet).
Ett helt binärt sökträd kan lätt passeras i ordning efter huvudnyckeln, men om man bara får en pekare till en nod kan det vara långsamt eller omöjligt att hitta den nod som kommer härnäst. Till exempel har lövnoder per definition inga avkomlingar, så om du bara får en pekare till en lövnod kan ingen annan nod nås. Ett gängat träd lägger till extra information i några eller alla noder, så att för varje given enskild nod kan "nästa" nod hittas snabbt, vilket tillåter trädpassering utan rekursion och den extra lagring (proportionell mot trädets djup) som rekursion kräver.
Träning
"Ett binärt träd trådas genom att alla höger underordnade pekare som normalt skulle vara noll pekar på nodens efterföljare i ordning ( om den finns), och alla vänster underordnade pekare som normalt skulle vara noll pekar på föregångaren i ordningsföljd av noden."
Detta förutsätter att korsningsordningen är densamma som genomgången av trädet. Dock kan pekare istället (eller i tillägg) läggas till trädnoder, snarare än att ersätta dem. Länkade listor som definieras på detta sätt kallas också vanligtvis "trådar" och kan användas för att möjliggöra genomgång i vilken ordning som helst. Till exempel kan ett träd vars noder representerar information om människor sorteras efter namn, men har extra trådar som tillåter snabb genomgång i ordning efter födelsedatum, vikt eller någon annan känd egenskap.
Motivering
Träd, inklusive (men inte begränsat till) binära sökträd , kan användas för att lagra objekt i en viss ordning, till exempel värdet av någon egenskap som lagras i varje nod, ofta kallad nyckel . En användbar operation på ett sådant träd är traversering : besöka alla objekt i nyckelordning.
En enkel rekursiv traversalalgoritm som besöker varje nod i ett binärt sökträd är följande. Antag att t är en pekare till en nod, eller noll . "Besöka" t kan innebära att utföra vilken åtgärd som helst på noden t eller dess innehåll.
Algoritmövergång( t ):
- Indata: en pekare t till en nod (eller noll )
- Om t = noll , returnera.
- Annan:
- travers(vänster-barn( t ))
- Besök t
- travers(höger-barn( t ))
Ett problem med denna algoritm är att den, på grund av dess rekursion, använder stackutrymme proportionellt mot höjden på ett träd. Om trädet är ganska balanserat, motsvarar detta O (log n ) utrymme för ett träd som innehåller n element. I värsta fall, när trädet tar formen av en kedja , är trädets höjd n så algoritmen tar O ( n ) utrymme. Ett andra problem är att alla övergångar måste börja vid roten när noder endast har pekare till sina barn. Det är vanligt att ha en pekare till en viss nod, men det räcker inte för att komma tillbaka till resten av trädet om inte extra information läggs till, såsom trådpekare.
I detta tillvägagångssätt är det kanske inte möjligt att avgöra om vänster- och/eller högerpekarna i en given nod faktiskt pekar på barn, eller är en konsekvens av trådning. Om distinktionen är nödvändig räcker det att lägga till en enda bit till varje nod för att spela in den.
I en lärobok från 1968 frågade Donald Knuth om det finns en icke-rekursiv algoritm för genomgång i ordning, som inte använder någon stack och lämnar trädet oförändrat. En av lösningarna på detta problem är trädtrådning, presenterad av Joseph M. Morris 1979. I 1969 års uppföljningsutgåva tillskrev Knuth den gängade trädrepresentationen till Perlis och Thornton (1960).
Relation till föräldrapekare
Ett annat sätt att uppnå liknande mål är att inkludera en pekare i varje nod, till den nodens överordnade nod. Med tanke på det kan "nästa" nod alltid nås. "rätt" pekare är fortfarande null när det inte finns några rätt barn. För att hitta "nästa" nod från en nod vars högra pekare är noll, gå upp genom "förälder"-pekare tills du når en nod vars högra pekare inte är null, och inte är barnet du just kom från. Den noden är "nästa" nod, och efter den kommer dess ättlingar till höger.
Det är också möjligt att upptäcka föräldern till en nod från ett gängat binärt träd, utan explicit användning av överordnade pekare eller en stack, även om det är långsammare. För att se detta, överväg en nod k med höger underordnade r . Då måste den vänstra pekaren för r vara antingen ett barn eller en tråd tillbaka till k . I det fall att r har ett vänsterbarn måste det vänstra barnet i sin tur ha antingen ett eget vänsterbarn eller en tråd tillbaka till k , och så vidare för alla efterföljande vänsterbarn. Så genom att följa kedjan av vänsterpekare från r kommer vi så småningom att hitta en tråd som pekar tillbaka till k . Situationen är symmetriskt likartad när q är det vänstra barnet till p - vi kan följa qs högra barn till en tråd som pekar framåt mot p .
I Python :
def parent ( nod ): om nod är nod . träd . root : return Ingen x = nod y = nod medan True : if is_thread ( y ): p = y . höger om p är Ingen eller p . vänster är inte nod : p = x medan det inte är_tråd ( s . vänster ): p = p . vänster p = p . vänster retur p elif is_thread ( x ): p = x . vänster om p är Ingen eller p . höger är inte nod : p = y medan inte är_tråd ( s . höger ): p = p . höger p = p . höger retur p x = x . vänster y = y . höger
Typer
- Enkelgängad: varje nod är gängad mot antingen föregångaren eller efterföljaren i sin ordning (vänster eller höger).
- Dubbelgängad: varje nod är gängad mot både föregångaren och efterföljaren i sin ordning (vänster och höger).
Uppsättningen av genomgång i ordning
Trådar är referenser till nodens föregångare och efterföljare enligt en inordnadsövergång.
i ordning är A,B,C,D,E,F,G,H,I, föregångaren till E är D , efterföljaren till E är F .
Exempel
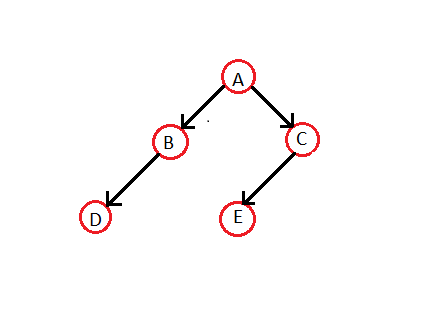
Låt oss göra det gängade binära trädet av ett normalt binärt träd:
Traverseringen i ordning för ovanstående träd är — DBAE C. Så det respektive gängade binära trädet kommer att vara --
Null länkar
I ett m -vägs gängat binärt träd med n noder finns det n × m − ( n −1) tomrumslänkar.