Mrs Minivers problem

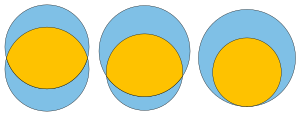
Tre fall av Mrs Minivers problem. I varje fall är det inre gula området lika med den totala arean av de omgivande blå regionerna. Det vänstra fallet visar två cirklar med lika stora ytor, det högra fallet visar en cirkel med dubbelt så stor yta som den andra, och mittfallet är mellanliggande mellan dessa två.

Mrs Minivers problem är ett geometriproblem om cirklarnas area . Den frågar hur man placerar två cirklar $A$ och $B$ med givna radier på ett sådant sätt att linsen som bildas genom att skära deras två interiörer har samma area som den symmetriska skillnaden för $A$ och $B$ (området som finns i en men inte båda cirklarna). Den fick sitt namn efter en analogi mellan geometri och social dynamik som uttalades av den fiktiva karaktären Mrs. Miniver , som "såg varje relation som ett par korsande cirklar". Dess lösning innebär en transcendental ekvation .

Ursprung

Problemet härrör från "A Country House Visit", en av Jan Struthers tidningsartiklar som förekom i Times of London mellan 1937 och 1939 med hennes karaktär Mrs. Miniver. Enligt historien:

Hon såg varje relation som ett par korsande cirklar. Det verkar vid första anblicken som att ju mer de överlappade desto bättre relation; men det är inte så. Bortom en viss punkt inträder lagen om minskande avkastning, och det finns inte tillräckligt med privata resurser kvar på någon sida för att berika livet som delas. Förmodligen uppnås perfektion när arean av de två yttre halvmånarna, adderade tillsammans, är exakt lika med den lövformade biten i mitten. På papper måste det finnas någon snygg matematisk formel för att komma fram till detta; i livet, ingen.

Louis A. Graham och Clifton Fadiman formaliserade problemets matematik och populariserade det bland fritidsmatematiker .

Lösning

Problemet kan lösas genom att skära av luna längs linjesegmentet mellan cirklarnas två korsningspunkter, i två cirkulära segment och använda formeln för arean av ett cirkulärt segment för att relatera avståndet mellan korsningspunkterna till den totala arean att problemet kräver att lune har. Detta ger en transcendental ekvation för avståndet mellan korsningspunkter men det kan lösas numeriskt. Det finns två randvillkor vars avstånd mellan centra lätt kan lösas: det längst ifrån varandra centran kan vara är när cirklarna har lika stora radier, och det närmaste de kan vara är när en cirkel är helt innesluten i den andra, vilket händer när förhållandet mellan radierna är ${\sqrt {2}}$ . Om förhållandet mellan radier faller utanför dessa begränsningsfall, kan cirklarna inte tillfredsställa problemets areabegränsning.

I fallet med två lika stora cirklar kan dessa ekvationer förenklas något. Romben som bildas av de två cirkelcentrumen och de två korsningspunkterna, med sidolängder lika med radien, har en vinkel $\theta \ca. 2.605$ radianer vid cirkelcentrumen, hittad genom att lösa ekvationen