Frågeoptimering

Frågeoptimering är en funktion i många relationsdatabashanteringssystem och andra databaser som NoSQL och grafdatabaser . Frågeoptimeraren försöker fastställa det mest effektiva sättet att utföra en given fråga genom att överväga möjliga frågeplaner .

Generellt kan frågeoptimeraren inte nås direkt av användare: när frågor har skickats till databasservern och analyserats av parsern skickas de sedan till frågeoptimeraren där optimering sker. Vissa databasmotorer tillåter dock att vägleda frågeoptimeraren med tips .

En fråga är en begäran om information från en databas. Det kan vara så enkelt som "hitta adressen till en person med personnummer 123-45-6789", eller mer komplext som "hitta medellönen för alla anställda gifta män i Kalifornien mellan 30 och 39 år som tjänar mindre än deras makar." Resultatet av en fråga genereras genom att raderna i en databas bearbetas på ett sätt som ger den begärda informationen. Eftersom databasstrukturer är komplexa, i de flesta fall, och särskilt för inte särskilt enkla frågor, kan den data som behövs för en fråga samlas in från en databas genom att komma åt den på olika sätt, genom olika datastrukturer och i olika ordningsföljder. Varje sätt kräver vanligtvis olika behandlingstid. Behandlingstider för samma fråga kan ha stor variation, från en bråkdel av en sekund till timmar, beroende på vald metod. Syftet med frågeoptimering, som är en automatiserad process, är att hitta sättet att bearbeta en given fråga på minimal tid. Den stora möjliga tidsvariationen motiverar att utföra frågeoptimering, även om att hitta den exakta optimala frågeplanen, bland alla möjligheter, vanligtvis är mycket komplex, tidskrävande i sig, kan vara för kostsamt och ofta praktiskt taget omöjligt. Således försöker frågeoptimering vanligtvis att approximera det optimala genom att jämföra flera sunt förnuftsalternativ för att inom rimlig tid tillhandahålla en "tillräckligt bra" plan som vanligtvis inte avviker mycket från det bästa möjliga resultatet.

Allmänna överväganden

Det finns en avvägning mellan mängden tid som ägnas åt att ta reda på den bästa frågeplanen och kvaliteten på valet; optimeraren kanske inte väljer det bästa svaret på egen hand. Olika kvaliteter hos databashanteringssystem har olika sätt att balansera dessa två. Kostnadsbaserade frågeoptimerare utvärderar resursavtrycket för olika frågeplaner och använder detta som grund för planval. Dessa tilldelar en uppskattad "kostnad" till varje möjlig frågeplan och väljer planen med den lägsta kostnaden. Kostnader används för att uppskatta körtidskostnaden för att utvärdera frågan, i termer av antalet I/O-operationer som krävs, CPU-sökvägslängd , mängden diskbuffertutrymme, disklagringstjänsttid och sammankopplingsanvändning mellan parallellitetsenheter och annat faktorer fastställda från dataordboken . Uppsättningen av frågeplaner som undersöks bildas genom att undersöka möjliga åtkomstvägar (t.ex. primär indexåtkomst, sekundär indexåtkomst, fullständig filsökning) och olika relationstabellsanslutningstekniker (t.ex. sammanfoga sammanfogning , hashanslutningar , produktanslutningar ) . Sökutrymmet kan bli ganska stort beroende på SQL -frågans komplexitet. Det finns två typer av optimering. Dessa består av logisk optimering – som genererar en sekvens av relationalgebra för att lösa frågan – och fysisk optimering – som används för att bestämma hur varje operation ska utföras.

Genomförande

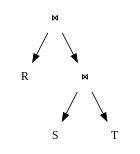
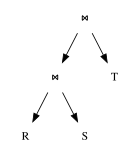
De flesta frågeoptimerare representerar frågeplaner som ett träd av "plannoder". En plannod kapslar in en enda operation som krävs för att exekvera frågan. Noderna är arrangerade som ett träd, i vilket mellanresultat flödar från botten av trädet till toppen. Varje nod har noll eller fler underordnade noder – det är noder vars utdata matas som indata till föräldernoden. Till exempel kommer en kopplingsnod att ha två underordnade noder, som representerar de två kopplingsoperanderna, medan en sorteringsnod skulle ha en enda undernod (indata som ska sorteras). Trädets löv är noder som ger resultat genom att skanna skivan, till exempel genom att utföra en indexskanning eller en sekventiell skanning.

Gå med i beställning

Två möjliga frågeplaner för triangelfrågan R(A, B) ⋈ S(B, C) ⋈ T(A, C) ; den första sammanfogar S och T först och sammanfogar resultatet med R , den andra sammanfogar R och S först och sammanfogar resultatet med T

Prestandan för en frågeplan bestäms till stor del av den ordning i vilken tabellerna sammanfogas. Till exempel, när du sammanfogar 3 tabeller A, B, C med storlek 10 rader, 10 000 rader respektive 1 000 000 rader, kan en frågeplan som sammanfogar B och C först ta flera storleksordningar längre tid att utföra än en som sammanfogar A och C först. De flesta frågeoptimerare bestämmer sammanfogningsordningen via en dynamisk programmeringsalgoritm som banat väg för IBM:s System R -databasprojekt . Denna algoritm fungerar i två steg:

1. Först beräknas alla sätt att komma åt varje relation i frågan. Varje relation i frågan kan nås via en sekventiell skanning. Om det finns ett index på en relation som kan användas för att svara på ett predikat i frågan, kan en indexskanning också användas. För varje relation registrerar optimeraren det billigaste sättet att skanna relationen, såväl som det billigaste sättet att skanna den relation som producerar poster i en viss sorterad ordning.
2. Optimeraren överväger sedan att kombinera varje par av relationer för vilka ett sammanfogningsvillkor existerar. För varje par kommer optimeraren att överväga de tillgängliga kopplingsalgoritmerna implementerade av DBMS . Det kommer att bevara det billigaste sättet att sammanfoga varje par av relationer, förutom det billigaste sättet att sammanfoga varje par av relationer som producerar sin produktion enligt en viss sorteringsordning.
3. Sedan beräknas alla frågeplaner med tre relationer genom att sammanfoga varje två-relationsplan som producerats av föregående fas med de återstående relationerna i frågan.

Sorteringsordning kan undvika en redundant sorteringsoperation senare vid bearbetning av frågan. För det andra kan en viss sorteringsordning påskynda en efterföljande koppling eftersom den kluster data på ett visst sätt.

Frågeplanering för kapslade SQL-frågor

En SQL-fråga till en modern relations-DBMS gör mer än bara urval och sammanfogningar. Särskilt SQL-frågor kapslar ofta flera lager av SPJ-block (Select-Project-Join), med hjälp av grupp efter , existerar och inte existerar operatorer. I vissa fall kan sådana kapslade SQL-frågor förenklas till en select-project-join-fråga, men inte alltid. Frågeplaner för kapslade SQL-frågor kan också väljas med samma dynamiska programmeringsalgoritm som används för join-order, men detta kan leda till en enorm eskalering av frågeoptimeringstiden. Så vissa databashanteringssystem använder ett alternativt regelbaserat tillvägagångssätt som använder en frågediagrammodell.

Kostnadsuppskattning

Ett av de svåraste problemen med frågeoptimering är att noggrant uppskatta kostnaderna för alternativa frågeplaner. Optimerare kostar frågeplaner med hjälp av en matematisk modell av utförandekostnader för frågor som i hög grad bygger på uppskattningar av kardinaliteten eller antalet tuplar som flödar genom varje kant i en frågeplan. Kardinalitetsuppskattningen beror i sin tur på uppskattningar av urvalsfaktorn för predikat i frågan. Traditionellt uppskattar databassystem selektivitet genom ganska detaljerad statistik om fördelningen av värden i varje kolumn, såsom histogram . Denna teknik fungerar bra för uppskattning av selektiviteter för individuella predikat. Men många frågor har konjunktioner av predikat som välj antal ( * ) från R där R . make = 'Honda' och R . modell = 'Accord' . Frågepredikat är ofta starkt korrelerade (till exempel, model='Accord' innebär make='Honda' ), och det är mycket svårt att uppskatta selektiviteten för konjunkten i allmänhet. Dåliga uppskattningar av kardinalitet och oupptäckt korrelation är en av huvudorsakerna till att frågeoptimerare väljer dåliga frågeplaner. Detta är en anledning till varför en databasadministratör regelbundet bör uppdatera databasstatistiken, särskilt efter större dataladdningar/avlastningar.

Tillägg

Klassisk frågeoptimering förutsätter att frågeplaner jämförs enligt ett enda kostnadsmått, vanligtvis exekveringstid, och att kostnaden för varje frågeplan kan beräknas utan osäkerhet. Båda antagandena bryts ibland i praktiken och flera förlängningar av klassisk frågeoptimering har studerats i forskningslitteraturen som övervinner dessa begränsningar. Dessa utökade problemvarianter skiljer sig åt i hur de modellerar kostnaden för plan för enstaka frågeställningar och i termer av deras optimeringsmål.

Parametrisk frågeoptimering

Klassisk frågeoptimering associerar varje frågeplan med ett skalärt kostnadsvärde. Parametrisk frågeoptimering förutsätter att kostnaden för frågeplanen beror på parametrar vars värden är okända vid optimeringstillfället. Sådana parametrar kan till exempel representera selektiviteten hos frågepredikat som inte är helt specificerade vid optimeringstidpunkten men kommer att tillhandahållas vid exekveringstidpunkten. Parametrisk frågeoptimering associerar därför varje frågeplan med en kostnadsfunktion som mappar från ett flerdimensionellt parameterutrymme till ett endimensionellt kostnadsutrymme.

Målet med optimering är vanligtvis att generera alla frågeplaner som kan vara optimala för någon av de möjliga parametervärdeskombinationerna. Detta ger en uppsättning relevanta frågeplaner. Vid körning väljs den bästa planen ur den uppsättningen när de sanna parametervärdena blir kända. Fördelen med parametrisk frågeoptimering är att optimering (vilket i allmänhet är en mycket dyr operation) undviks under körning.

Flerobjektiv frågeoptimering

Det finns ofta andra kostnadsmått utöver exekveringstiden som är relevanta för att jämföra frågeplaner. I ett molnberäkningsscenario bör man till exempel jämföra frågeplaner inte bara när det gäller hur mycket tid de tar att köra utan också när det gäller hur mycket pengar de kostar. Eller i samband med ungefärlig frågeoptimering är det möjligt att exekvera frågeplaner på slumpmässigt utvalda prover av indata för att erhålla ungefärliga resultat med minskad exekveringsoverhead. I sådana fall måste alternativa frågeplaner jämföras med avseende på deras exekveringstid men också när det gäller precisionen eller tillförlitligheten hos de data de genererar.

Multi-objektiv frågeoptimering modellerar kostnaden för en frågeplan som en kostnadsvektor där varje vektorkomponent representerar kostnad enligt ett annat kostnadsmått. Klassisk frågeoptimering kan betraktas som ett specialfall av multi-objektiv frågeoptimering där dimensionen av kostnadsutrymmet (dvs. antalet kostnadsvektorkomponenter) är en.

Olika kostnadsmått kan komma i konflikt med varandra (t.ex. kan det finnas en plan med minimal utförandetid och en annan plan med minimala monetära utförandeavgifter i ett molnberäkningsscenario). Därför kan målet med optimering inte vara att hitta en frågeplan som minimerar alla kostnadsmått utan måste vara att hitta en frågeplan som realiserar den bästa kompromissen mellan olika kostnadsmått. Vad den bästa kompromissen är beror på användarpreferenser (till exempel kanske vissa användare föredrar en billigare plan medan andra föredrar en snabbare plan i ett molnscenario). Målet med optimeringen är därför antingen att hitta den bästa frågeplanen baserat på någon specifikation av användarpreferenser som tillhandahålls som input till optimeraren (t.ex. kan användare definiera vikter mellan olika kostnadsmått för att uttrycka relativ betydelse eller definiera hårda kostnadsgränser för vissa mätvärden) eller för att generera en uppskattning av uppsättningen av Pareto-optimala frågeplaner (dvs. planer så att ingen annan plan har bättre kostnader enligt alla mätvärden) så att användaren kan välja den föredragna kostnadsavvägningen från den planuppsättningen.

Parametrisk frågeoptimering med flera mål

Multi-objektiv parametrisk frågeoptimering generaliserar parametrisk och multi-objektiv frågeoptimering. Planer jämförs enligt flera kostnadsmått och plankostnader kan bero på parametrar vars värden är okända vid optimeringstillfället. Kostnaden för en frågeplan modelleras därför som en funktion från ett flerdimensionellt parameterutrymme till ett flerdimensionellt kostnadsutrymme. Målet med optimering är att generera uppsättningen av frågeplaner som kan vara optimala för varje möjlig kombination av parametervärden och användarpreferenser.

Ett antal verktyg visar exekveringsplaner för frågor för att visa vilka operationer som har den högsta bearbetningskostnaden. Microsoft SMS, ApexSQLPlan, Hana och Tableau är några exempel. Att åtgärda dessa problem som finns i dessa planer kan sänka tiotals procents exekveringstid, och i vissa fall kan det minska tvådimensionella sökningar till linjära.

En av de primära och enklaste optimeringschecklistorna är att använda operationer som de flesta RDMS är designade för att utföra effektivt. Se Sargable .

Se även

• Gå med urvalsfaktor
• Fråga omskrivning
• Särgbar fråga