Emden–Chandrasekhar ekvation

Numerisk lösning av Emden-Chandrasekhars ekvation

Inom astrofysik är Emden -Chandrasekhar-ekvationen en dimensionslös form av Poisson-ekvationen för densitetsfördelningen av en sfäriskt symmetrisk isotermisk gassfär som utsätts för sin egen gravitationskraft, uppkallad efter Robert Emden och Subrahmanyan Chandrasekhar . Ekvationen introducerades först av Robert Emden 1907. Ekvationen lyder

{\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\vänster (\xi ^{2}{\frac {d\psi }{d\xi }}\right)=e^{-\psi }

där $\xi$ är den dimensionslösa radien och $\psi$ är relaterad till gassfärens densitet som $\rho =\rho _{c} e^{-\psi }$ , där $\rho _{c}$ är densiteten för gasen i mitten. Ekvationen har ingen känd explicit lösning. Om en polytropisk vätska används istället för en isotermisk vätska får man Lane–Emden-ekvationen . Det isotermiska antagandet modelleras vanligtvis för att beskriva kärnan i en stjärna. Ekvationen löses med initialvillkoren,

\psi =0,\quad {\frac {d\psi }{d\xi }}=0\quad {\text{at}}\quad \xi =0.

Ekvationen förekommer även i andra grenar av fysiken, till exempel förekommer samma ekvation i Frank-Kamenetskii explosionsteorin för ett sfäriskt kärl. Den relativistiska versionen av denna sfäriskt symmetriska isotermiska modell studerades av Subrahmanyan Chandrasekhar 1972.

Härledning

För en isotermisk gasformig stjärna beror trycket $p$ på det kinetiska trycket och strålningstrycket

p=\rho {\frac {k_{B}}{WH}}T+{\frac {4\sigma }{3c}}T^ {4}

wh

$\rho$ är densiteten
$k_{B}$ är Boltzmann-konstanten
$W$ är medelmolekylvikten
$H$ är protonens massa
$T$ är stjärnans temperatur
$\sigma$ är Stefan–Boltzmann-konstanten
$c$ är ljusets hastighet

Ekvationen för stjärnans jämvikt kräver en balans mellan tryckkraften och gravitationskraften

{\frac {1}{r^{2}}}{\frac {d}{dr}}\vänster ({\frac {r^{2}}{\rho }}{\frac {dp}{dr}}\right)=-4\pi G\rho

där $r$ är radien mätt från mitten och $G$ är gravitationskonstanten . Ekvationen skrivs om som

{\frac {k_{B}T}{WH}}{\frac {1} {r^{2}}}{\frac {d}{dr}}\left(r^{2}{\frac {d\ln \rho }{dr}}\right)=-4\pi G\ rho

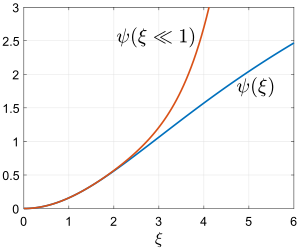
Faktisk lösning och asymptotisk lösning

Introduktion av förvandlingen

\psi =\ln {\frac {\rho _{c}}{\rho }} ,\quad \xi =r\left({\frac {4\pi G\rho _{c}WH}{k_{B}T}}\right)^{1/2}

där $\rho _{c}$ är stjärnans centrala täthet, leder till

{\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\vänster (\xi ^{2}{\frac {d\psi }{d\xi }}\right)=e^{-\psi }

Gränsvillkoren är

\psi =0,\quad {\frac {d\psi }{d\xi }}=0\quad {\text{at}}\quad \xi =0

För $\xi \ll 1$ blir lösningen som

\psi ={\frac {\xi ^{2}}{6}}-{\frac {\xi ^{4}}{120 }}+{\frac {\xi ^{6}}{1890}}+\cdots

Modellens begränsningar

Att anta en isotermisk sfär har vissa nackdelar. Även om densiteten som erhålls som lösning av denna isotermiska gassfär minskar från centrum, minskar den för långsamt för att ge en väldefinierad yta och ändlig massa för sfären. Det kan visas att, eftersom $\xi \gg 1$ ,

{\frac {\rho }{\ rho _{c}}}=e^{-\psi }={\frac {2}{\xi ^{2}}}\left[1+{\frac {A}{\xi ^{1/2 }}}\cos \left({\frac {\sqrt {7}}{2}}\ln \xi +\delta \right)+O(\xi ^{-1})\right]

där $A$ och $\delta$ är konstanter som kommer att erhållas med numerisk lösning. Detta densitetsbeteende ger upphov till ökning i massa med ökning av radien. Således är modellen vanligtvis giltig för att beskriva stjärnans kärna, där temperaturen är ungefär konstant.

Singular lösning

Genom att introducera transformationen $x=1/\xi$ transformeras ekvationen till

x^{4}{\frac {d^{2}\psi }{dx^{2}}}=e^{-\psi }

Ekvationen har en singularis lösning som ges av

e^{-\psi _{s}}=2x^{2},\quad {\text{eller }}\quad -\psi _{s}=2\ln x+\ln 2

Därför kan en ny variabel introduceras som $-\psi =2\ln x+z$ , där ekvationen för $z$ kan härledas,

{\frac {d^{2}z}{dt^{2}}}-{\frac {dz}{dt}}+e^{z}-2=0,\quad {\text{där}}\quad t=\ln x

Denna ekvation kan reduceras till första ordningen genom att införa

y={\frac {dz}{dt}}=\xi {\frac {d\psi }{d\xi }}-2

då har vi

y{\frac {dy}{dz}}-y+e^{z}-2=0

Minskning

Det finns ytterligare en minskning på grund av Edward Arthur Milne . Låt oss definiera

u={\frac {\xi e^{-\psi }}{d\psi /d\xi }},\ quad v=\xi {\frac {d\psi }{d\xi }}

sedan

{\frac {u}{v}}{\frac {dv}{du}}=-{\frac {u-1}{ u+v-3}}

Egenskaper

Om $\psi (\xi )$ är en lösning till Emden–Chandrasekhars ekvation, då $\psi (A\xi )-2\ln A$ är också en lösning av ekvationen, där $A$ är en godtycklig konstant.
Lösningarna av Emden–Chandrasekhar-ekvationen som är finita vid origo har nödvändigtvis $d\psi /d\xi =0$ vid $\xi =0$

Se även