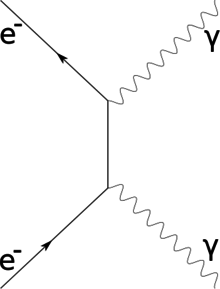
Elektronspridning

Typer av spridning
Bildbeskrivning av hur en elektronstråle kan interagera med ett prov med kärna N, och elektronmoln av elektronskal K,L,M. Visar överförda elektroner och elastiska/oelastiskt spridda elektroner. SE är en sekundär elektron som skjuts ut av strålelektronen och avger en karakteristisk foton (röntgen) γ . BSE är en bakåtriktad elektron , en elektron som sprids bakåt istället för att sändas genom provet .
Elektron ( e − , β − )
Partikel	Elektron
Massa	9,109 382 91 (40) × 10 −31 kg   5,485 799 0946 (22) × 10 −4 u [ 1 822 ,888 4845 (14) ] −1 u 0,510 998 928 / c12) MeV ( 12 )
Elektrisk laddning	−1 e   −1,602 176 565 (35) × 10 −19 C   −4,803 204 51 (10) × 10 −10 esu
Magnetiskt ögonblick	−1,001 159 652 180 76(27) μ B
Snurra	1⁄2 _ _
Spridning
Krafter/effekter	Lorentzkraft , Elektrostatisk kraft , Gravitation , Svag interaktion
Åtgärder	Laddning , ström
Kategorier	Elastisk kollision , Oelastisk kollision , Hög energi , Låg energi
Interaktioner	e − — e − e − — γ e − — e + e − — p e − — n e − — Kärnor
Typer	Compton-spridning Møller-spridning Mott-spridning Bhabha-spridning Bremsstrahlung Djup oelastisk spridning Synkrotronemission Thomson-spridning

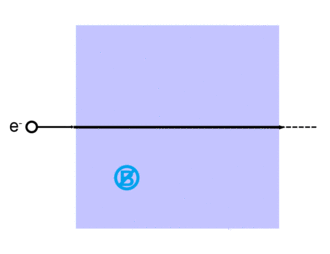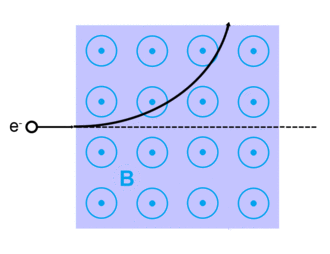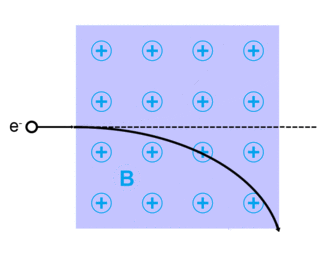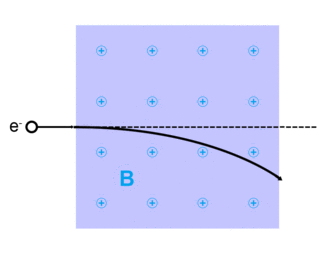
Elektronspridning uppstår när elektroner avviker från sin ursprungliga bana . Detta beror på de elektrostatiska krafterna inom materiainteraktion eller, om ett externt magnetfält är närvarande, kan elektronen avböjas av Lorentzkraften . Denna spridning sker vanligtvis med fasta ämnen som metaller, halvledare och isolatorer; och är en begränsande faktor i integrerade kretsar och transistorer.

Tillämpningen av elektronspridning är sådan att den kan användas som ett högupplöst mikroskop för hadroniska system, som möjliggör mätning av fördelningen av laddningar för nukleoner och kärnstruktur . Spridningen av elektroner har gjort det möjligt för oss att förstå att protoner och neutroner består av de mindre elementära subatomära partiklarna som kallas kvarkar .

Elektroner kan spridas genom ett fast ämne på flera sätt:

• Inte alls : ingen elektronspridning inträffar alls och strålen passerar rakt igenom.
• Enkelspridning : när en elektron sprids bara en gång.
• Plural spridning : när elektron(er) sprids flera gånger.
• Multipel spridning : när elektron(er) sprids många gånger om.

Sannolikheten för en elektronspridning och graden av spridning är en sannolikhetsfunktion av provets tjocklek till den genomsnittliga fria banan.

Historia

Principen om elektronen teoretiserades först under perioden 1838-1851 av en naturfilosof vid namn Richard Laming som spekulerade i förekomsten av subatomära enhetsladdade partiklar; han föreställde också atomen som en "elektrosfär" av koncentriska skal av elektriska partiklar som omger en materiell kärna.

Det är allmänt accepterat att JJ Thomson först upptäckte elektronen 1897, även om andra anmärkningsvärda medlemmar i utvecklingen av laddade partikelteori är George Johnstone Stoney (som myntade termen "elektron"), Emil Wiechert (som var den första att publicera sin oberoende upptäckt av elektronen), Walter Kaufmann , Pieter Zeeman och Hendrik Lorentz .

Comptonspridning observerades första gången vid Washington University i St Louis 1923 av Arthur Compton som fick 1927 års Nobelpris i fysik för upptäckten; hans doktorand YH Woo som ytterligare verifierade resultaten är också att nämna. Compton-spridning nämns vanligtvis med hänvisning till interaktionen som involverar elektronerna i en atom, men nukleär Compton-spridning existerar.

Det första elektrondiffraktionsexperimentet utfördes 1927 av Clinton Davisson och Lester Germer med vad som skulle komma att bli en prototyp för moderna LEED -system. Experimentet kunde demonstrera de vågliknande egenskaperna hos elektroner, vilket bekräftade de Broglies hypotes att materiapartiklar har en vågliknande natur. Emellertid efter detta minskade intresset för LEED till förmån för högenergielektrondiffraktion fram till början av 1960-talet då intresset för LEED återupplivades; av anmärkningsvärt omnämnande under denna period är HE Farnsworth som fortsatte att utveckla LEED-tekniker.

Historien om högenergielektron-elektronkolliderande strålar börjar 1956 när K. O'Neill från Princeton University blev intresserad av högenergikollisioner och introducerade idén om accelerator(er) som injicerade i lagringsring(ar). Medan idén om strål-strålekollisioner hade funnits sedan ungefär 1920-talet, var det inte förrän 1953 som ett tyskt patent på kolliderande strålapparater erhölls av Rolf Widerøe .

Fenomen

Se även: Kvantelektrodynamik

Elektroner kan spridas av andra laddade partiklar genom de elektrostatiska Coulomb-krafterna. Dessutom, om ett magnetfält är närvarande, kommer en vandringselektron att avböjas av Lorentzkraften. En extremt noggrann beskrivning av all elektronspridning, inklusive kvant- och relativistiska aspekter, ges av teorin om kvantelektrodynamik.

Lorentz kraft

Banan för en elektron med hastighet v som rör sig i ett magnetfält B . Där den prickade cirkeln indikerar magnetfältet riktat ut ur planet, och den korsade cirkeln indikerar magnetfältet riktat in i planet.

Huvudartikel: Lorentz kraft

Lorentzkraften, uppkallad efter den holländska fysikern Hendrik Lorentz , för en laddad partikel q ges (i SI-enheter) av ekvationen:

$\mathbf {F} =q\mathbf {E} +q\mathbf {v} \times \mathbf {B}$

där q E beskriver den elektriska kraften på grund av ett närvarande elektriskt fält, E , som verkar på q . Och q v x B beskriver den magnetiska kraften på grund av ett närvarande magnetfält, B , som verkar på q när q rör sig med hastigheten v . Vilket också kan skrivas som:

$\mathbf {F} =q[-\nabla \phi -{\frac {d\mathbf {A} }{dt }}+\nabla (\mathbf {A} \cdot \mathbf {v} )]$

där $\phi$ är den elektriska potentialen och A är den magnetiska vektorpotentialen .

Det var Oliver Heaviside som 1885 och 1889 tillskrivs att först härleda det korrekta uttrycket för Lorentz-kraften av q v x B . Hendrik Lorentz härledde och förfinade konceptet 1892 och gav det sitt namn, med krafter från elektriska fält. Om man skriver om detta som rörelseekvationen för en fri laddningspartikel q massa m , blir detta:

$m{\frac {d\mathbf {v} }{dt}}=q\mathbf {E} +q\mathbf {v} \times \mathbf {B}$

eller

$m{\frac {d\gamma \mathbf {v} }{dt}}=q\mathbf {E} +q\mathbf {v} \ gånger \mathbf {B}$

i det relativistiska fallet med Lorentz kontraktion där γ är:

$\gamma (v)\equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$

denna rörelseekvation verifierades första gången 1897 i JJ Thomsons experiment som undersökte katodstrålar som bekräftade, genom böjning av strålarna i ett magnetfält, att dessa strålar var en ström av laddade partiklar som nu kallas elektroner.

Variationer på denna grundläggande formel beskriver den magnetiska kraften på en strömförande tråd (ibland kallad Laplace-kraft), den elektromotoriska kraften i en trådslinga som rör sig genom ett magnetfält (en aspekt av Faradays induktionslag) och kraften på en partikel som kan färdas nära ljusets hastighet (relativistisk form av Lorentz-kraften).

Elektrostatisk Coulomb-kraft

Det absoluta värdet av kraften F mellan två punktladdningar q och Q relaterar till avståndet r mellan punktladdningarna och till den enkla produkten av deras laddningar. Diagrammet visar att lika laddningar stöter bort varandra, och motsatta laddningar attraherar varandra.

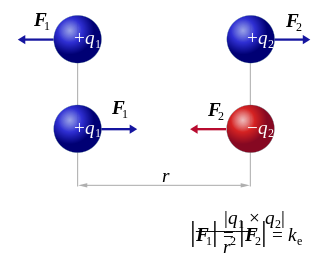
I bilden är vektorn F ₁ kraften som upplevs av q ₁ , och vektorn F ₂ är kraften som upplevs av q ₂ . När q ₁ q ₂ > 0 är krafterna frånstötande (som på bilden) och när q ₁ q ₂ < 0 är krafterna attraktiva (motsatsen till bilden). Storleken på krafterna kommer alltid att vara lika stor. I detta fall: $\mathbf {F} =k{\frac {q_{1}q_{2}}{|\mathbf {r_{12}} |^{2}}}\mathbf {\hat { r_{12}}} ={\frac {q_{1}q_{2}}{4\pi \epsilon _{0}|\mathbf {r_{12}} |^{2}}}\mathbf {\ hatt {r_{12}}}$ där vektorn, ${\boldsymbol {r_{12}}}={\boldsymbol {r_{1}-r_{2}}}$ är vektoravståndet mellan laddningarna och, ${\displaystyle {\boldsymbol {{\hat {r}}_{12}}}={{\boldsymbol {r_{12}}}/|{\boldsymbol {r_{12}}}|}} (en$ enhet vektor som pekar från q ₂ till q ₁ ). Vektorformen av ekvationen ovan beräknar kraften F ₁ som appliceras på q ₁ med q ₂ . Om r ₂₁ används istället, så kan effekten på q ₂ hittas. Det kan också beräknas med hjälp av Newtons tredje lag : F ₂ = - F ₁ .

Huvudartikel: Coulombs lag

Elektrostatisk Coulomb-kraft även känd som Coulomb-interaktion och elektrostatisk kraft , uppkallad efter Charles-Augustin de Coulomb som publicerade resultatet 1785, beskriver attraktionen eller avstötningen av partiklar på grund av deras elektriska laddning.

Coulombs lag säger att:

Storleken på den elektriska kraften mellan två punktladdningar är direkt proportionell mot produkten av laddningarna och omvänt proportionell mot kvadraten på avståndet mellan dem.

Storleken på den elektrostatiska kraften är proportionell mot den skalära multipeln av laddningsstorlekarna och omvänt proportionell mot kvadraten på avståndet (dvs. omvänd kvadratisk lag ) , och ges av:

$F=k{\frac {|q_{1}q_{2}|}{r^{2}}}={\frac {|q_{1}q_{2}|} {4\pi \epsilon _{0}r^{2}}}$

eller i vektornotation:

$\mathbf {F} =k{\frac {q_{1}q_{2}}{|\mathbf {r} |^{2}}}\mathbf {\hat {r}} = {\frac {q_{1}q_{2}}{4\pi \epsilon _{0}|\mathbf {r} |^{2}}}\mathbf {\hat {r}}$

där q ₁ , q ₂ är två undertecknade punktladdningar; r-hatten är enhetsvektorriktningen för avståndet r mellan laddningar; k är Coulombs konstant och ε ₀ är permittiviteten för fritt utrymme, givet i SI-enheter av:

$k={\frac {1}{4\pi \epsilon _{0}}}\approx 8.988\times 10^{9} Nm^{2}{C^{-}}^{2}$

$\epsilon _{0}\approx 8.854\times 10^{- 12}C^{2}N^{-1}m^{-2}$

Riktningarna för de krafter som utövas av de två laddningarna på varandra är alltid längs den räta linjen som förenar dem (det kortaste avståndet), och är vektorkrafter med oändligt räckvidd; och lyda Newtons 3:e lag är lika stor och i motsatt riktning. Vidare, när båda laddningarna q ₁ och q ₂ har samma tecken (antingen båda positiva eller båda negativa) är krafterna mellan dem frånstötande, om de har motsatt tecken är krafterna attraktiva. Dessa krafter följer en viktig egenskap som kallas principen för överlagring av krafter som säger att om en tredje laddning infördes så är den totala kraften som verkar på den laddningen vektorsumman av de krafter som skulle utövas av de andra laddningarna individuellt, detta gäller för valfritt antal avgifter. Emellertid har Coulombs lag angetts för laddningar i ett vakuum , om utrymmet mellan punktladdningar innehåller materia måste permittiviteten för saken mellan laddningarna redovisas enligt följande:

$F=k{\frac {|q_{1}q_{2}|}{\epsilon _{r}r^{2}}}$

där εr _som är den relativa permittiviteten eller dielektricitetskonstanten för det utrymme kraften verkar genom, och är dimensionslös.

Kollisioner

Om två partiklar interagerar med varandra i en spridningsprocess finns två möjliga resultat efter interaktionen:

Elastisk

Se även: Elastisk spridning

Elastisk spridning är när kollisioner mellan mål och infallande partiklar har total bevarande av kinetisk energi. Detta innebär att det inte sker någon uppbrytning av partiklarna eller energiförlust genom vibrationer, det vill säga att de inre tillstånden för var och en av partiklarna förblir oförändrade. På grund av det faktum att det inte finns något brott, kan elastiska kollisioner modelleras som att de inträffar mellan punktliknande partiklar, en princip som är mycket användbar för en elementarpartikel som elektronen.

Oelastisk

Se även: Oelastisk spridning

Oelastisk spridning är när kollisionerna inte bevarar kinetisk energi, och som sådan har de inre tillstånden för en eller båda partiklarna förändrats. Detta beror på att energi omvandlas till vibrationer som kan tolkas som värme, vågor (ljud) eller vibrationer mellan ingående partiklar från endera kollisionsparten. Partiklar kan också splittras, ytterligare energi kan omvandlas till att bryta de kemiska bindningarna mellan komponenter.

Dessutom bevaras momentum i både elastisk och oelastisk spridning. Andra resultat än spridning är reaktioner, i vilka strukturen hos de interagerande partiklarna förändras och producerar två eller fler allmänt komplexa partiklar, och skapandet av nya partiklar som inte utgör elementarpartiklar i de interagerande partiklarna.

Andra typer av spridning

Elektron-molekylspridning

Elektronspridning av isolerade atomer och molekyler sker i gasfasen. Det spelar en nyckelroll inom plasmafysik och kemi och det är viktigt för sådana tillämpningar som halvledarfysik. Elektron-molekyl/atomspridning behandlas normalt med hjälp av kvantmekanik. Den ledande metoden för att beräkna tvärsnitten är att använda R-matrismetoden .

Compton-spridning

Compton-spridning Feynman-diagram

Huvudartikel: Compton-spridning

Compton scattering , så uppkallad efter Arthur Compton som först observerade effekten 1922 och som gav honom 1927 års Nobelpris i fysik; är den oelastiska spridningen av en högenergifoton av en fri laddad partikel.

Detta demonstrerades 1923 genom att avfyra strålning med en given våglängd (röntgenstrålar i det givna fallet) genom en folie (kolmål), som spreds på ett sätt som inte överensstämmer med klassisk strålningsteori. Compton publicerade en artikel i Physical Review som förklarade fenomenet: En kvantteori om spridningen av röntgenstrålar av lätta element . Comptoneffekten kan förstås som högenergifotoner som sprider in-elastiskt från enskilda elektroner, när den inkommande fotonen ger en del av sin energi till elektronen, då har den spridda fotonen lägre energi och lägre frekvens och längre våglängd enligt Planck- relationen :

$E=h\nu =hf$

vilket ger energin E för fotonen i termer av frekvens f eller ν , och Plancks konstant h ( 6,626 × 10 ⁻³⁴ J⋅s = 4,136 × 10 ⁻¹⁵ eV.s ). Våglängdsändringen i sådan spridning beror endast på spridningsvinkeln för en given målpartikel.

Detta var en viktig upptäckt under 1920-talet när ljusets partikel (foton) natur som föreslogs av den fotoelektriska effekten fortfarande diskuterades, Compton-experimentet gav tydliga och oberoende bevis på partikelliknande beteende.

Formeln som beskriver Compton-förskjutningen i våglängden på grund av spridning ges av:

$\lambda _{f}-\lambda _{i}={\frac {h}{m_{e}c}}(1 -\cos \theta )$

där λ _f är den slutliga våglängden för fotonen efter spridning, λ _i är den initiala våglängden för fotonen före spridning, h är Plancks konstant, m _e är elektronens vilomassa, c är ljusets hastighet och θ är spridningsvinkel för fotonen.

Koefficienten för (1 - cos θ) är känd som Compton-våglängden , men är i själva verket en proportionalitetskonstant för våglängdsförskjutningen. Kollisionen gör att fotonvåglängden ökar med någonstans mellan 0 (för en spridningsvinkel på 0°) och två gånger Comptons våglängd (för en spridningsvinkel på 180°).

Thomson-spridning är den klassiska elastiska kvantitativa tolkningen av spridningsprocessen, och detta kan ses hända med fotoner med lägre medelenergi. Den klassiska teorin om en elektromagnetisk våg spridd av laddade partiklar kan inte förklara lågintensitetsförskjutningar i våglängd.

Invers Compton-spridning sker när elektronen rör sig och har tillräcklig kinetisk energi jämfört med fotonen. I detta fall kan nettoenergin överföras från elektronen till fotonen. Den omvända Compton-effekten ses inom astrofysik när en lågenergifoton (t.ex. av den kosmiska mikrovågsbakgrunden) studsar av en högenergielektron (relativistisk). Sådana elektroner produceras i supernovor och aktiva galaktiska kärnor.

Møller spridning

Møller sprider Feynman-diagram

Huvudartikel: Møller spridning

Mott spridning

Huvudartikel: Mott spridning

Bhabha-spridning

Huvudartikel: Bhabha-spridning

Bremsstrahlung spridning

Huvudartikel: Bremsstrahlung

Djup oelastisk spridning

Huvudartikel: Djup oelastisk spridning

Synkrotronemission

Huvudartikel: Synkrotronemission

Om en laddad partikel som en elektron accelereras – det kan vara acceleration i en rak linje eller rörelse i en krökt bana – sänds ut elektromagnetisk strålning av partikeln. Inom elektronlagringsringar och cirkulära partikelacceleratorer som kallas synkrotroner , böjs elektroner i en cirkulär bana och avger typiskt röntgenstrålar. Denna radiellt utsända ( $\mathbf {a} \perp \mathbf {v}$ ) elektromagnetiska strålning när laddade partiklar accelereras kallas synkrotronstrålning . Den tillverkas i synkrotroner med hjälp av böjningsmagneter, undulatorer och/eller wigglers .

Den första observationen kom vid General Electric Research Laboratory i Schenectady, New York, den 24 april 1947, i synkrotronen byggd av ett team av Herb Pollack för att testa idén om fasstabilitetsprincipen för RF-acceleratorer. När teknikern ombads se sig omkring i skärmningen med en stor spegel för att kontrollera om det fanns gnistor i röret, såg han en ljus båge av ljus som kom från elektronstrålen. Robert Langmuir är krediterad för att känna igen det som synkrotronstrålning eller, som han kallade det, "Schwinger-strålning" efter Julian Schwinger .

Klassiskt är den utstrålade effekten P från en accelererad elektron:

$P={\frac {2Ke^{2}}{3c^{2}}}a^{2}$

detta kommer från Larmor-formeln ; där K är en elektrisk permittivitetskonstant, e är elektronladdning, c är ljusets hastighet och a är accelerationen. Inom en cirkulär bana som en lagringsring är det icke-relativistiska fallet helt enkelt centripetalaccelerationen. Men inom en lagringsring är accelerationen mycket relativistisk och kan erhållas enligt följande:

$a_{icke-relativistisk}={\frac {v^{2}}{r}}\rightarrow a_{relativistic}={\ frac {1}{m}}{\frac {dp}{d\tau }}={\frac {1}{m}}\gamma {\frac {d(\gamma mv)}{dt}}=\ gamma ^{2}{\frac {dv}{dt}}=\gamma ^{2}{\frac {v^{2}}{r}}$ ,

där v är den cirkulära hastigheten, r är radien för den cirkulära acceleratorn, m är den laddade partikelns vilomassa, p är rörelsemängden, τ är den korrekta tiden (t/γ) och γ är Lorentz-faktorn . Utstrålad kraft blir då:

$P={\frac {2Ke^{2}}{3c^{ 2}}}({\frac {\gamma ^{2}v^{2}}{r}})^{2}={\frac {2Ke^{2}}{3c^{2}}}{ \frac {\gamma ^{4}v^{4}}{r^{2}}}$

För mycket relativistiska partiklar, så att hastigheten blir nästan konstant, blir γ4- ^termen den dominerande variabeln vid bestämning av förlusthastighet, vilket betyder att förlusten skalar som fjärde potensen av partikelenergin ^γmc2 ; och det omvända beroendet av synkrotronstrålningsförlust på radien talar för att acceleratorn ska byggas så stor som möjligt.

Faciliteter

SLAC

Se även: SLAC National Accelerator Laboratory

Flygfoto av Stanford Linear Accelerator Center, med detektorkomplex på höger (östra) sida

Stanford Linear Accelerator Center ligger nära Stanford University , Kalifornien. Konstruktionen började på den 2 mil långa linjäracceleratorn 1962 och slutfördes 1967, och 1968 upptäcktes det första experimentella beviset på kvarkar, vilket resulterade i 1990 års Nobelpris i fysik, delat av SLAC:s Richard Taylor och Jerome I. Friedman och Henry Kendall från MIT. Acceleratorn kom med en kapacitet på 20 GeV för elektronaccelerationen, och även om den liknade Rutherfords spridningsexperiment, fungerade det experimentet med alfapartiklar vid endast 7 MeV. I SLAC-fallet var den infallande partikeln en elektron och målet en proton, och på grund av elektronens korta våglängd (på grund av dess höga energi och momentum) kunde den sondera in i protonen. Stanford Positron Electron Asymmetric Ring (SPEAR) tillägget till SLAC gjorde ytterligare sådana upptäckter möjliga, vilket ledde till upptäckten 1974 av J/psi-partikeln, som består av en parad charmkvark och anti-charm-kvark, och ytterligare ett Nobelpris i Fysik 1976. Detta följdes upp med Martin Perls tillkännagivande om upptäckten av tau leptonen, för vilken han delade 1995 års Nobelpris i fysik.

SLAC strävar efter att vara ett främsta acceleratorlaboratorium, för att bedriva strategiska program inom partikelfysik, partikelastrofysik och kosmologi, såväl som tillämpningarna för att upptäcka nya läkemedel för helande, nya material för elektronik och nya sätt att producera ren energi och städa upp miljö. Under ledning av Chi-Chang Kao, SLAC:s femte chef (från och med november 2012), en känd röntgenforskare som kom till SLAC 2010 för att fungera som biträdande laboratoriechef för Stanford Synchrotron Radiation Lightsource.

BaBar

Se även: BaBar-experiment

SSRL - Stanford Synchrotron Radiation Lightsource

Se även: Stanford Synchrotron Radiation Lightsource

Andra vetenskapliga program som körs på SLAC inkluderar:

• Avancerad acceleratorforskning
• ATLAS/Large Hadron Collider
• Elementarpartikelteori
• EXO - Enriched Xenon Observatory
• FACET - Facilitet för avancerade acceleratorexperimentella tester
• Fermi Gamma-ray rymdteleskop
• Geant4
• KIPAC - Kavli-institutet för partikelastrofysik och kosmologi
• LCLS - Linac Coherent Light Source
• LSST - Large Synoptic Survey Telescope
• NLCTA - Next Linear Collider Test Accelerator
• Stanford PULSE Institute
• SIMES - Stanford Institute for Materials and Energy Sciences
• SUNCAT Center for Interface Science and Catalysis
• Super CDMS - Super Cryogenic Dark Matter Search

RIKEN RI Beam Factory

Se även: Radioactive Isotope Beam Factory

RIKEN grundades 1917 som en privat forskningsstiftelse i Tokyo och är Japans största omfattande forskningsinstitution. Efter att ha vuxit snabbt i storlek och omfattning är det idag känt för högkvalitativ forskning inom en mängd olika vetenskapliga discipliner, och omfattar ett nätverk av forskningscentra och institut i världsklass över hela Japan.

RIKEN RI Beam Factory , även känd som RIKEN Nishina Center (för acceleratorbaserad vetenskap), är en cyklotronbaserad forskningsanläggning som började fungera 2007; 70 år efter den första i japanska cyklotronen, från Dr. Yoshio Nishina vars namn ges till anläggningen.

Från och med 2006 har anläggningen ett acceleratorkomplex med tunga joner i världsklass. Denna består av en K540-MeV ringcyklotron (RRC) och två olika injektorer: en variabel frekvens tung-jon linac (RILAC) och en K70-MeV AVF cyklotron (AVF). Den har en projektil-fragmentseparator (RIPS) som ger RI-strålar (Radioactive Isotope) på mindre än 60 amu, världens mest intensiva RI-strålar med lätt atommassa.

Övervakad av Nishina Centre, används RI Beam Factory av användare över hela världen som främjar forskning inom kärn-, partikel- och hadronfysik. Detta främjande av forskning om acceleratortillämpningar är ett viktigt uppdrag för Nishina Centre, och implementerar användningen av både inhemska och utländska acceleratoranläggningar.

SCRIT

Se även: SCRIT

SCRIT -anläggningen (Self-Confining Radioactive Isotope Ion Target) är för närvarande under uppbyggnad vid RIKEN RI strålfabriken (RIBF) i Japan. Projektet syftar till att undersöka kortlivade kärnor genom användning av ett elastiskt elektronspridningstest av laddningstäthetsfördelning, med initiala tester gjorda med stabila kärnor. Med den första elektronspridningen av instabila Sn-isotoper kommer att ske 2014.

Undersökningen av kortlivade radioaktiva kärnor (RI) med hjälp av elektronspridning har aldrig utförts på grund av en oförmåga att göra dessa kärnor till ett mål, nu med tillkomsten av en ny självbegränsande RI-teknik vid världens första anläggning avsedd för studiet av strukturen hos kortlivade kärnor genom elektronspridning denna forskning blir möjlig. Principen för tekniken är baserad på jonfångningsfenomenet som observeras vid elektronlagringsringanläggningar, vilket har en negativ effekt på elektronlagringsringarnas prestanda.

Den nya idén som ska användas vid SCRIT är att använda joninfångningen för att tillåta kortlivade RI att göras till ett mål, som fångade joner på elektronstrålen, för spridningsexperimenten. Denna idé fick först en proof-of-principle-studie med användning av elektronlagringsringen vid Kyoto University, KSR; detta gjordes med hjälp av en stabil kärna på ¹³³ Cs som mål i ett experiment med 120MeV elektronstråleenergi, 75mA typisk lagrad strålström och en strållivslängd på 100 sekunder. Resultaten av denna studie var gynnsamma med elastiskt spridda elektroner från de fångade Cs som var tydligt synliga.

Se även

• Zeeman effekt
• Partikelfysik
• Lågenergi elektrondiffraktion
• Kvantelektrodynamik
• R-matris

externa länkar

• Physics Out Loud: Electron Scattering (video)
• Brightstorm: Compton Scattering (video)