Dining kryptografer problem

Inom kryptografi studerar restaurangkryptografernas problem hur man utför en säker flerpartsberäkning av den booleska XOR-funktionen. David Chaum föreslog detta problem först i början av 1980-talet och använde det som ett illustrativt exempel för att visa att det var möjligt att skicka anonyma meddelanden med ovillkorlig avsändare och mottagare ospårbarhet. Anonyma kommunikationsnätverk baserade på detta problem kallas ofta för DC-nät (där DC står för "dining cryptographers").

Trots ordet middag är problemet med dining kryptografer inte relaterat till dining philosophers problem .

Beskrivning

Dining kryptografer problem illustration

Tre kryptografer samlas runt ett bord för middag. Servitören informerar dem om att måltiden har betalats av någon, som kan vara en av kryptograferna eller National Security Agency ( NSA). Kryptograferna respekterar varandras rätt att göra en anonym betalning, men vill ta reda på om NSA betalat. Så de bestämmer sig för att köra ett tvåstegsprotokoll.

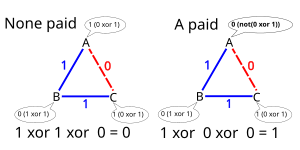
I det första steget etablerar varannan kryptograf en delad enbitshemlighet, t.ex. genom att kasta ett mynt bakom en meny så att endast två kryptografer ser resultatet i tur och ordning för var och en av två kryptografer. Anta till exempel att efter myntkastningen delar kryptograf A och B en hemlig bit $1$ , A och C delar $0$ och B och C delar $1$ .

I det andra steget tillkännager varje kryptograf offentligt en bit, vilket är:

• om de inte betalade för måltiden, det exklusiva OR (XOR) av de två delade bitarna som de har med sina två grannar,
• om de betalade för måltiden, motsatsen till den XOR.

Om du antar att ingen av kryptograferna betalade, då meddelar A ${\displaystyle 1\oplus 0=1} ,$ B tillkännager $1\oplus 1=0$ , och C tillkännager ${ \displaystyle 0\oplus 1=1}$ . Å andra sidan, om A betalade, meddelar hon $\lnot (1\oplus 0)=0$ .

De tre offentliga tillkännagivandena tillsammans avslöjar svaret på deras fråga. Man beräknar helt enkelt XOR för de tre aviserade bitarna. Om resultatet är 0, innebär det att ingen av kryptograferna betalade (så NSA måste ha betalat räkningen). Annars betalade en av kryptograferna, men deras identitet förblir okänd för de andra kryptograferna.

David Chaum myntade termen dining cryptographers network , eller DC-net, för detta protokoll.

Begränsningar

DC-net-protokollet är enkelt och elegant. Det har flera begränsningar, men några lösningar har undersökts i uppföljningsforskningen (se avsnittet Referenser nedan).

Kollision

Om två kryptografer betalade för middagen kommer deras meddelanden att ta bort varandra och det slutliga XOR-resultatet blir {\ $displaystyle 0}$ . Detta kallas en kollision och tillåter endast en deltagare att sända åt gången med detta protokoll. I ett mer allmänt fall sker en kollision så länge som ett jämnt antal deltagare skickar meddelanden.

Störning

Alla illvilliga kryptografer som inte vill att gruppen ska kommunicera framgångsrikt kan blockera protokollet så att det slutliga XOR-resultatet är värdelöst, helt enkelt genom att skicka slumpmässiga bitar istället för det korrekta resultatet av XOR. Det här problemet uppstår eftersom det ursprungliga protokollet utformades utan att använda någon offentlig nyckelteknologi och saknar tillförlitliga mekanismer för att kontrollera om deltagarna ärligt följer protokollet.

Komplexitet

Protokollet kräver parvis delade hemliga nycklar mellan deltagarna, vilket kan vara problematiskt om det är många deltagare. Även om DC-net-protokollet är "villkorslöst säkert", beror det faktiskt på antagandet att "villkorslöst säkra" kanaler redan finns mellan par av deltagare, vilket inte är lätt att uppnå i praktiken.

En relaterad anonym vetonätverksalgoritm beräknar det logiska ELLER för flera användares ingångar snarare än en logisk XOR som i DC-nät, vilket kan vara användbart i applikationer för vilka en logisk ELLER-kombinationsoperation är naturligt lämpad.

Historia

David Chaum tänkte först på detta problem i början av 1980-talet. Den första publikationen som beskriver de grundläggande bakomliggande idéerna är hans. Journalversionen dök upp i det allra första numret av Journal of Cryptology.

Generaliseringar

DC-nät är lätt generaliserade för att tillåta överföringar av mer än en bit per omgång, för grupper större än tre deltagare, och för godtyckliga "alfabet" andra än de binära siffrorna 0 och 1, som beskrivs nedan.

Sändningar av längre meddelanden

För att göra det möjligt för en anonym avsändare att sända mer än en bit information per DC-nätrunda, kan gruppen av kryptografer helt enkelt upprepa protokollet så många gånger som önskas för att skapa ett önskat antal bitar värt överföringsbandbredd. Dessa repetitioner behöver inte utföras i serie. I praktiska DC-nätsystem är det typiskt för par av deltagare att komma överens på förhand om en enda delad "huvudhemlighet", till exempel med hjälp av Diffie–Hellman-nyckelutbyte . Varje deltagare matar sedan lokalt in denna delade huvudhemlighet i en pseudoslumptalsgenerator för att producera så många delade "myntvändningar" som önskas för att tillåta en anonym avsändare att sända flera bitar av information.

Större gruppstorlekar

Protokollet kan generaliseras till en grupp av $n$ deltagare, var och en med en delad hemlig nyckel gemensam med varje annan deltagare. I varje omgång av protokollet, om en deltagare vill sända ett ospårbart meddelande till gruppen, inverterar de sin offentligt tillkännagivna bit. Deltagarna kan visualiseras som en helt sammankopplad graf där hörnen representerar deltagarna och kanterna representerar deras delade hemliga nycklar.

Glesna grafer för hemlighetsdelning

Protokollet kan köras med mindre än fullt anslutna grafer för hemlighetsdelning, vilket kan förbättra prestandan och skalbarheten för praktiska DC-net-implementeringar, med risk för att minska anonymiteten om samverkande deltagare kan dela upp grafen för hemlighetsdelning i separata anslutna komponenter. Till exempel en intuitivt tilltalande men mindre säker generalisering till $n>3$ deltagare som använder en ringtopologi , där varje kryptograf som sitter runt ett bord delar en hemlighet endast med kryptografen till vänster och höger omedelbart, och inte med varannan kryptograf. En sådan topologi är tilltalande eftersom varje kryptograf behöver koordinera två myntvändningar per omgång, snarare än $n$ . Men om Adam och Charlie faktiskt är NSA-agenter som sitter omedelbart till vänster och höger om Bob, ett oskyldigt offer, och om Adam och Charlie i hemlighet samarbetar för att avslöja sina hemligheter för varandra, då kan de med säkerhet avgöra om Bob var eller inte avsändaren av en 1 bit i en DC-net-körning, oavsett hur många deltagare det är totalt. Detta beror på att de samarbetande deltagarna Adam och Charlie effektivt "delar upp" grafen för hemlighetsdelning i två separata frånkopplade komponenter, den ena innehåller bara Bob, den andra innehåller alla andra ärliga deltagare.

En annan kompromisshemlighetsdelning DC-nättopologi, som används i Dissent -systemet för skalbarhet, kan beskrivas som en klient/server eller en användare/förvaltare topologi. I denna variant antar vi att det finns två typer av deltagare som spelar olika roller: ett potentiellt stort antal n användare som önskar anonymitet och ett mycket mindre antal $m$ förvaltare vars roll är att hjälpa användarna att få den anonymiteten . I denna topologi delar var och en av de $n$ -användarna en hemlighet med var och en av de $m$ -förvaltarna – men användare delar inga hemligheter direkt med andra användare, och förvaltare delar inga hemligheter direkt med andra förvaltare – vilket resulterar i i en $n\ gånger m$ hemlig delningsmatris. Om antalet förvaltare $m$ är litet behöver varje användare endast hantera ett fåtal delade hemligheter, vilket förbättrar effektiviteten för användarna på samma sätt som ringtopologin gör. Men så länge som minst en förvaltare uppträder ärligt och inte läcker sina hemligheter eller samarbetar med andra deltagare, så bildar den ärliga förvaltaren ett "nav" som kopplar samman alla ärliga användare till en enda fullt ansluten komponent, oavsett vilken eller hur många andra användare och/eller förvaltare kan samarbeta på ett oärligt sätt. Användare behöver inte veta eller gissa vilken förvaltare som är ärlig; deras säkerhet beror endast på att det finns minst en ärlig, icke-samverkande förvaltare.

Alternativa alfabet och kombinera operatorer

Även om det enkla DC-nets-protokollet använder binära siffror som överföringsalfabet och använder XOR-operatorn för att kombinera chiffertexter, generaliserar det grundläggande protokollet till alla alfabet och kombinationsoperatörer som är lämpliga för engångskodkryptering . Denna flexibilitet uppstår naturligt från det faktum att hemligheterna som delas mellan de många paren av deltagare i själva verket bara är engångsblock som kombineras symmetriskt inom en enda DC-nätrunda.

Ett användbart alternativt val av DC-näts alfabet och kombinationsoperator är att använda en finit grupp som lämpar sig för kryptografi med publik nyckel som alfabetet – såsom en Schnorr-grupp eller elliptisk kurva – och att använda den tillhörande gruppoperatorn som DC-nätkombinationen operatör. Ett sådant val av alfabet och operatör gör det möjligt för klienter att använda noll-kunskapssäker teknik för att bevisa korrekthetsegenskaper för DC-net-chiffertexterna som de producerar, som att deltagaren inte "stoppar" överföringskanalen, utan att kompromissa med anonymitet som erbjuds av DC-net. Denna teknik föreslogs först av Golle och Juels, vidareutvecklad av Franck, och senare implementerad i Verdict , en kryptografiskt verifierbar implementering av Dissent -systemet.

Hantera eller undvika kollisioner

Åtgärden som ursprungligen föreslogs av David Chaum för att undvika kollisioner är att återsända meddelandet när en kollision upptäcks, men tidningen förklarar inte exakt hur man ska ordna omsändningen.

Oliktänkande undviker möjligheten till oavsiktliga kollisioner genom att använda en verifierbar shuffle för att upprätta ett DC-näts överföringsschema, så att varje deltagare vet exakt vilka bitar i schemat som motsvarar hans egen överföringslucka, men inte vet vem som äger andra överföringsluckor.

Motverka störningsattacker

Herbivore delar upp ett stort anonymitetsnätverk i mindre DC-nätgrupper, vilket gör det möjligt för deltagare att undvika störningsförsök genom att lämna en störd grupp och gå med i en annan grupp, tills deltagaren hittar en grupp fri från störande ämnen. Denna flyktstrategi introducerar risken att en motståndare som äger många noder selektivt kan störa endast grupper som motståndaren inte helt har kompromissat, och därigenom "valla" deltagarna mot grupper som kan vara funktionella just för att de är helt komprometterade.

Oliktänkande implementerar flera system för att motverka störningar. Det ursprungliga protokollet använde en verifierbar kryptografisk blandning för att bilda ett DC-net-överföringsschema och distribuera "överföringsuppdrag", vilket gjorde det möjligt att verifiera korrektheten av efterföljande DC-näts chiffertexter med en enkel kryptografisk hashkontroll . Denna teknik krävde en ny verifierbar innan varje DC-nätrunda, vilket dock ledde till höga latenser. Ett senare, mer effektivt schema tillåter en serie DC-net-rundor att fortsätta utan ingripande shufflingar i frånvaro av avbrott, men som svar på en störningshändelse använder man en shuffle för att distribuera anonyma anklagelser som gör det möjligt för ett avbrottsoffer att avslöja och bevisa identiteten på gärningsmannen. Slutligen, nyare versioner stöder fullt verifierbara DC-nät - till betydande kostnad i beräkningseffektivitet på grund av användningen av public-key kryptografi i DC-nätet - såväl som ett hybridläge som använder effektiva XOR-baserade DC-nät i normalfall och verifierbara DC-nät endast vid avbrott, för att sprida anklagelser snabbare än vad som är möjligt med verifierbara shufflar.