Dela-och-härska egenvärdesalgoritm

Dela-och-härska egenvärdesalgoritmer är en klass av egenvärdesalgoritmer för hermitiska eller reella symmetriska matriser som nyligen (cirka 1990-talet) har blivit konkurrenskraftiga när det gäller stabilitet och effektivitet med mer traditionella algoritmer som QR-algoritmen . Grundkonceptet bakom dessa algoritmer är dela-och-härska- metoden från datavetenskap . Ett egenvärdesproblem delas upp i två problem med ungefär hälften så stora problem, vart och ett av dessa löses rekursivt och egenvärdena för det ursprungliga problemet beräknas från resultaten av dessa mindre problem.

Här presenterar vi den enklaste versionen av en dela-och-härska-algoritm, liknande den som ursprungligen föreslogs av Cuppen 1981. Många detaljer som ligger utanför denna artikels ram kommer att utelämnas; men utan att beakta dessa detaljer är algoritmen inte helt stabil.

Bakgrund

Som med de flesta egenvärdesalgoritmer för hermitiska matriser börjar dividera-och-härska med en reduktion till tridiagonal form. För en ${\displaystyle m\times m} matris$ tar standardmetoden för detta, via Householder reflections , ${\frac {4}{3}}m^{3}$ flytande punktoperationer, eller ${\frac {8}{3}}m^{3}$ om egenvektorer också behövs. Det finns andra algoritmer, såsom Arnoldi-iterationen , som kan fungera bättre för vissa klasser av matriser; vi kommer inte att överväga detta mer här.

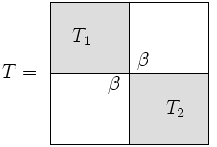
I vissa fall är det möjligt att deflatera ett egenvärdesproblem till mindre problem. Betrakta en blockdiagonal matris

$T={\begin{bmatrix}T_{1}&0\\0&T_{2}\end{bmatrix}}.$

Egenvärdena och egenvektorerna för $T$ är helt enkelt de för $T_{1}$ och $T_{2}$ , och det kommer nästan alltid att gå snabbare att lösa dessa två mindre problem än att lösa det ursprungliga problemet på en gång. Denna teknik kan användas för att förbättra effektiviteten hos många egenvärdealgoritmer, men den har speciell betydelse för dela-och-härska.

För resten av den här artikeln kommer vi att anta att ingången till divide-and-conquer-algoritmen är en $m\times m$ reell symmetrisk tridiagonal matris $T$ . Även om algoritmen kan modifieras för hermitiska matriser, ger vi inte detaljerna här.

Dela upp

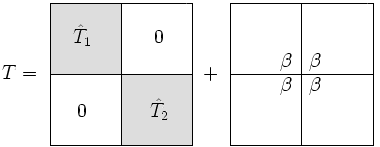
Dela - delen av dela-och-härska-algoritmen kommer från insikten att en tridiagonal matris är "nästan" blockdiagonal.

Storleken på submatrisen $T_{1}$ kallar vi $n\ gånger n$ , och då är $T_{2}$$(mn)\times (mn)$ . Observera att anmärkningen om att $T$ är nästan blockdiagonal är sant oavsett hur $n$ väljs (dvs det finns många sätt att bryta ner matrisen). Men ur effektivitetssynpunkt är det vettigt att välja $n\approx m/2$ .

Vi skriver $T$ som en blockdiagonal matris, plus en rank-1- korrigering:

Den enda skillnaden mellan $T_{1}$ och ${\hat {T}}_{1}$ är att den nedre högra posten $t_{nn}$ i ${\hat {T}}_{1}$ ersatts med $t_{nn}-\beta$ och på liknande sätt, i ${ \hat {T}}_{2}$ den övre vänstra posten $t_{n+1,n+1}$ har ersatts med $t_{n+1,n+1}-\beta$ .

Resten av delningssteget är att lösa för egenvärdena (och om så önskas egenvektorerna) för ${\hat {T}}_{1}$ och ${\hat {T }}_{2}$ , det vill säga att hitta diagonaliseringarna ${\hat {T}}_{1}=Q_{1}D_{1}Q_{ 1}^{T}$ och ${\hat {T}}_{2}=Q_{2}D_{2}Q_{2}^{T}$ . Detta kan åstadkommas med rekursiva anrop till dela-och-härska-algoritmen, även om praktiska implementeringar ofta byter till QR-algoritmen för tillräckligt små submatriser.

Erövra

Erövringsdelen av algoritmen är den ointuitiva delen . Med tanke på diagonaliseringen av submatriserna, beräknade ovan, hur hittar vi diagonaliseringen av den ursprungliga matrisen?

Definiera först ${\displaystyle z^{T}=(q_{1}^{T},q_{2}^{T})} ,$ där ${ \displaystyle q_{1}^{T}}$ är den sista raden i $Q_{1}$ och $q_{2}^{T}$ är den första raden i ${ \displaystyle Q_{2}}$ . Det är nu elementärt att visa det

$T={\begin{bmatrix}Q_{1}&\\&Q_{2 }\end{bmatrix}}\left({\begin{bmatrix}D_{1}&\\&D_{2}\end{bmatrix}}+\beta zz^{T}\right){\begin{bmatrix} Q_{1}^{T}&\\&Q_{2}^{T}\end{bmatrix}}$

Den återstående uppgiften har reducerats till att hitta egenvärdena för en diagonal matris plus en rang-1-korrigering. Innan vi visar hur man gör detta, låt oss förenkla notationen. Vi letar efter egenvärdena för matrisen $D+ww^{T}$ , där $D$ är diagonal med distinkta poster och $w$ är vilken vektor som helst som inte är noll poster.

Fallet med en nollpost är enkelt, eftersom om w _i är noll, ( ${\displaystyle e_{i}} ,$ di ₎ är ett egenpar ( $e_{i}$ är i standardbasen ) av $D+ww^{T}$ eftersom $(D+ww^{T})e_ {i}=De_{i}=d_{i}e_{i}$ .

Om $\lambda$ är ett egenvärde har vi:

$(D+ww^{T})q=\lambda q$

där $q$ är motsvarande egenvektor. Nu

$(D-\lambda I)q+w(w^{T}q)=0$

$q+(D-\lambda I)^{-1}w(w^{T}q)=0$

$w^{T}q+w^{T}(D-\lambda I)^{-1}w(w^{T}q)=0$

Tänk på att $w^{T}q$ är en skalär som inte är noll. Varken $w$ eller $q$ är noll. Om $w^{T}q$ skulle vara noll, skulle $q$ vara en egenvektor för $D$ med ${\ displaystil (D+ww^{T})q=\lambda q}$ . Om så var fallet $q$ endast innehålla en position som inte är noll eftersom $D$ är distinkt diagonal och därför kan den inre produkten $w^{T}q$ inte vara noll trots allt. Därför har vi:

$1+w^{T}(D-\lambda I)^{-1}w=0$

eller skriven som en skalär ekvation,

$1+\sum _{j=1}^{m}{\frac {w_{j}^{2}}{d_{ j}-\lambda }}=0.$

Denna ekvation är känd som den sekulära ekvationen . Problemet har därför reducerats till att hitta rötterna till den rationella funktion som definieras av den vänstra sidan av denna ekvation.

Alla allmänna egenvärdesalgoritmer måste vara iterativa, och dela-och-härska-algoritmen är inte annorlunda. Att lösa den olinjära sekulära ekvationen kräver en iterativ teknik, såsom Newton-Raphson-metoden . Varje rot kan dock hittas i O (1) iterationer, som var och en kräver $\Theta (m)$ floppar (för en $m$ -graders rationell funktion), vilket gör kostnaden av den iterativa delen av denna algoritm $\Theta (m^{2})$ .

Analys

Som är vanligt för dela och erövra algoritmer kommer vi att använda mastersatsen för dividera-och-härska upprepningar för att analysera löptiden. Kom ihåg att vi ovan angav att vi väljer $n\approx m/2$ . Vi kan skriva återfallsrelationen :

$T(m)=2\gånger T\left({\frac {m}{2}}\right)+\Theta ( m^{2})$

I beteckningen för Mastersatsen, $a=b=2$ och därmed $\log _{b}a=1$ . Tydligen ${\displaystyle \Theta (m^{2})=\Omega (m^{1})} ,$ så vi har

$T(m)=\Theta (m^{2})$

Kom ihåg att vi ovan påpekade att reducering av en hermitisk matris till tridiagonal form tar ${\frac {4}{3}}m^{3}$ floppar. Detta försämrar körtiden för dela-och-härska-delen, och vid denna tidpunkt är det inte klart vilken fördel dela-och-härska-algoritmen erbjuder jämfört med QR-algoritmen (som också tar Θ ( m 2 $Theta (m^{2})}$ floppar för tridiagonala matriser).

Fördelen med dela-och-härska kommer när egenvektorer också behövs. Om så är fallet tar reduktion till tridiagonal form ${\frac {8}{3}}m^{3}$ , men den andra delen av algoritmen tar ${\ displaystyle \Theta (m^{3})}$ också. För QR-algoritmen med en rimlig målprecision är detta $\approx 6m^{3}$ , medan det för divide-and-conquer är $\approx {\frac {4}{3}}m^{3}$ . Anledningen till denna förbättring är att i divide-and-hera är ${\displaystyle \Theta (m^{3})}-$ delen av algoritmen (multiplicera $Q$ -matriser) skild från iterationen, medan i QR måste detta ske i varje iterativt steg. Lägger man till de ${\frac {8}{3}}m^{3}$ flopparna för minskningen, är den totala förbättringen från $\approx 9m^{3}$ till $\approx 4m^{3}$ floppar.

Praktisk användning av dela-och-härska-algoritmen har visat att i de flesta realistiska egenvärdeproblem gör algoritmen faktiskt bättre än så här. Anledningen är att matriserna $Q$ och vektorerna ${\displaystyle z} väldigt ofta$ tenderar att vara numeriskt glesa , vilket innebär att de har många poster med värden mindre än flyttalsprecisionen, vilket tillåter numerisk deflation , dvs. dela upp problemet i okopplade delproblem.

Varianter och genomförande

Algoritmen som presenteras här är den enklaste versionen. I många praktiska implementeringar används mer komplicerade rank-1-korrigeringar för att garantera stabilitet; vissa varianter använder till och med rank-2-korrigeringar.

Det finns specialiserade rotsökningstekniker för rationella funktioner som kan göra bättre än Newton-Raphson-metoden när det gäller både prestanda och stabilitet. Dessa kan användas för att förbättra den iterativa delen av dela-och-härska-algoritmen.

Dela-och-härska-algoritmen kan lätt parallelliseras , och linjära algebra- beräkningspaket som LAPACK innehåller parallella implementeringar av hög kvalitet.

•    Demmel, James W. (1997), Applied Numerical Linear Algebra , Philadelphia, PA: Society for Industrial and Applied Mathematics , ISBN 0-89871-389-7 , MR 1463942 .
• Cuppen, JJM (1981). "En dela och erövra metod för det symmetriska tridiagonala egenproblemet". Numerisk Mathematik . 36 : 177-195.